angles in a triangle problem solving

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Angles In A Triangle

Here is everything you need to know about angles in a triangle including what the angles in a triangle add up to, how to find missing angles, and how to use this alongside other angle facts to form and solve equations.

There are also angles in a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are angles in a triangle?

All triangles have interior angles that add up to 180º .

Angles in a triangle are the sum (total) of the angles at each vertex in a triangle.

We can use this fact to calculate missing angles by finding the total of the given angles and subtracting it from 180º .

This is true for all types of triangles.

• Right Angle Triangle: One 90° angle, the other two angles will have a total of 90° .
• Isosceles Triangle: Two equal sides and angles.
• Equilateral Triangle: All three angles are 60° .
• Scalene Triangle: All three angles are different.

How to find a missing angle in a triangle

In order to find the missing angle in a triangle:

• Add up the other angles within the triangle.
• Subtract this total from 180º .

Explain how to find a missing angle in a triangle in 2 steps

Angles in a triangle worksheet

Get your free angles in a triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on angles in polygons

Angles in a triangle  is part of our series of lessons to support revision on  angles in polygons . You may find it helpful to start with the main angles in polygons lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Angles in polygons
• Interior angles of a polygon
• Exterior angles of a polygon
• Angles in a quadrilateral
• Angles in a pentagon
• Angles in a hexagon

Finding missing angles examples

Example 1: scalene triangle.

Work out the size of the angle labelled a in the following triangle.

• We are given the angles 57º and 79º . Add these together.

2 Subtract 136º from 180º .

Example 2: right angled triangle

Find the angle labelled b in the following triangle.

We are given the angles 90º and 19º . Add these together.

Subtract 109º from 180º .

Example 3: isosceles triangle

Find the angle labelled c in the following triangle.

When two sides of a triangle are equal, the angles at the ends of those sides will also be equal.

We are given the angle 64º. As this is an isosceles triangle (two equal length sides and two equal angles), the other angle at the bottom will also be 64º .

Subtract 128º from 180º .

How to find one of the two equal angles in an isosceles triangle

• Subtract the given angle from 180º .
• Divide by 2 .

Example 4: equal angles in an isosceles triangle

Find the size of the angle labelled d in the triangle below.

This is an isosceles triangle. We are given one angle and asked to find one of the remaining two angles, which we know are equal.

The other two angles in this triangle add up to 70º .

Since the other two angles in this triangle are equal, we can find d by dividing by 2 .

How to use angle facts to solve problems

Sometimes the problem will involve using other angle facts. Let’s recap some of the other angle facts we know:

• Use angle facts to fill in any possible angles.
• Use these angles to calculate missing angles in the triangle.

These steps are interchangeable and may need to be repeated for more difficult problems.

Example 5: using angles at a point

Find the size of the angle labelled e .

Here we can use the fact that angles at a point add up to 360º .

Now we know two angles within the triangle, we can find the missing angle.

Example 6: using opposite angles

This time we already know two of the angles in the triangle so we can start by finding the third angle.

We can use the fact that opposite angles are equal to find f .

Example 7: two different triangles

Find the size of the angle labelled g .

We know two of the angles in the right hand triangle and so we can calculate the third.

We can use the fact that angles on a straight line add up to 180º .

Since the sides of the triangle are equal, the left hand triangle is an isosceles triangle and the two angles at the bottom of the triangle are equal. Therefore we can work out the third angle.

How to work out angles in a triangle with algebra

We can use the fact that the angles in a triangle add up to 180º to form equations which we can then solve to find the values of the angles in the triangle.

•  Add together the expressions for each angle and simplify.
•  Put the simplified expression equal to 180º .

Solve the equation.

•  Substitute your value back in to find the angles in the triangle.

Example 8: angles involving algebra

Find the size of each angle in this triangle.

Add the expressions for each angle.

Put the simplified expression equal to 180º .

Work out the angles.

The three angles are 40º , 60º and 80º .

Example 9: angles involving algebra

Find the size of each angle in this right-angled triangle.

The three angles are 23º , 67º and 90º .

Common misconceptions

• Incorrect angle sum

Using 360º instead of 180º for the sum of the angles of the triangle.

• Equal angles in an isosceles triangle

Selecting the wrong angles when identifying the equal angles in an isosceles triangle (particularly a problem when the equal angles are not at the bottom). The angle that is different in an isosceles triangle is the one between the two sides with equal length.

Practice angles in a triangle questions

1. Find the angle labelled z in the following triangle.

2. Find the angle labelled y .

This is an isosceles triangle and the two angles at the bottom of the triangle are equal.

3. Find the angle x in the following triangle.

This is an isosceles triangle and the two angles on the right are equal.

4.  What is the size of each angle in an equilateral triangle?

All three angles in an equilateral triangle are equal so

5. Find the size of the angle labelled w in the following triangle.

The angle opposite 24^{\circ} is also 24^{\circ} since vertically opposite angles are equal.

The triangle is an isosceles triangle and the two angles on the left are the same size.

6.  Find the angle labelled v .

Looking at the left hand triangle frist, we can find the missing angle in that triangle:

We can then use the fact that angles on a straight line add up to 180^{\circ} to find the unlabelled angle in the right hand triangle:

We can then find angle v :

7. Write an equation involving u and use it to find the size of each angle in the following triangle.

Adding the expressions gives us:

Angles in a triangle GCSE questions

1. Find the size of angle x given that the exterior angle shown is 153^{\circ} .

2. (a) Calculate the size of angle ACE .

(b) Show that BCD is an isosceles triangle.

90 + 36 = 126  

            (1)

180-126=54^{\circ}  

Angle CBD :

= 180 – 117  

=63^{\circ}    

Angle BDC : 

63 + 54 = 117

180-117=63^{\circ}

Two angles equal therefore isosceles                

3. Work out the size of the smallest angle in the right angled triangle.

3x – 10 + 2x + 55 + 90 (= 5x + 135)

5x + 135 = 180

3\times 9-10=17^{\circ}   

Learning checklist:

You have now learned how to:

• Use the sum of the angles of a triangle to find missing angles
• Apply other angle facts to find missing angles in triangle problems
• Form and solve equations using the sum of the angles in a triangle

The next lessons are

• Angle rules
• Angles in parallel lines
• How to calculate volume

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

Triangle Angle Calculator

Table of contents

Triangle angle calculator is a safe bet if you want to know how to find the angle of a triangle. Whether you have three sides of a triangle given, two sides and an angle or just two angles, this tool is a solution to your geometry problems. Below you'll also find the explanation of fundamental laws concerning triangle angles: triangle angle sum theorem, triangle exterior angle theorem, and angle bisector theorem. Read on to understand how the calculator works, and give it a go - finding missing angles in triangles has never been easier!

How to find the angle of a triangle

There are several ways to find the angles in a triangle, depending on what is given:

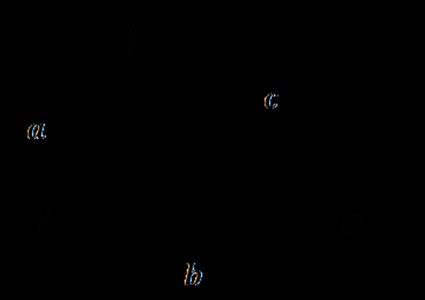
• Given three triangle sides

Use the formulas transformed from the law of cosines:

For the second angle we have:

And eventually, for the third angle:

• Given two triangle sides and one angle

If the angle is between the given sides, you can directly use the law of cosines to find the unknown third side, and then use the formulas above to find the missing angles, e.g. given a,b,γ:

• calculate c = a 2 + b 2 − 2 a b × cos ⁡ ( γ ) c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)} c = a 2 + b 2 − 2 ab × cos ( γ ) ​ ;
• substitute c c c in α = a r c c o s ( ( b 2 + c 2 − a 2 ) / ( 2 b c ) ) \alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right) α = arccos ( ( b 2 + c 2 − a 2 ) / ( 2 b c ) ) ;
• then find β \beta β from triangle angle sum theorem: β = 180 ° − α − γ \beta = 180\degree- \alpha - \gamma β = 180° − α − γ

If the angle isn't between the given sides, you can use the law of sines. For example, assume that we know a a a , b b b , and α \alpha α :

• As you know, the sum of angles in a triangle is equal to 180 ° 180\degree 180° . From this theorem we can find the missing angle: γ = 180 ° − α − β \gamma = 180\degree- \alpha - \beta γ = 180° − α − β .
• Given two angles

That's the easiest option. Simply use the triangle angle sum theorem to find the missing angle:

• α = 180 ° − β − γ \alpha = 180\degree- \beta - \gamma α = 180° − β − γ ;
• β = 180 ° − α − γ \beta= 180\degree- \alpha - \gamma β = 180° − α − γ ; and
• γ = 180 ° − α − β \gamma = 180\degree- \alpha- \beta γ = 180° − α − β

In all three cases, you can use our triangle angle calculator - you won't be disappointed.

🙋 Meet the law of sines and cosines at our law of cosines calculator and law of sines calculator ! Everything will be clear afterward. 😉

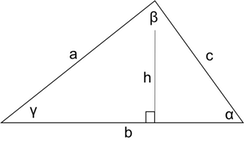
Sum of angles in a triangle - Triangle angle sum theorem

The theorem states that interior angles of a triangle add to 180 ° 180\degree 180° :

How do we know that? Look at the picture: the angles denoted with the same Greek letters are congruent because they are alternate interior angles. Sum of three angles α \alpha α β \beta β , γ \gamma γ is equal to 180 ° 180\degree 180° , as they form a straight line. But hey, these are three interior angles in a triangle! That's why α + β + γ = 180 ° \alpha + \beta+ \gamma = 180\degree α + β + γ = 180° .

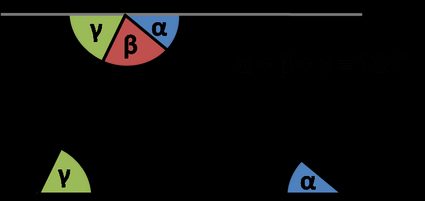
Exterior angles of a triangle - Triangle exterior angle theorem

An exterior angle of a triangle is equal to the sum of the opposite interior angles .

• Every triangle has six exterior angles (two at each vertex are equal in measure).
• The exterior angles, taken one at each vertex, always sum up to 360 ° 360\degree 360° .
• An exterior angle is supplementary to its adjacent triangle interior angle.

Angle bisector of a triangle - Angle bisector theorem

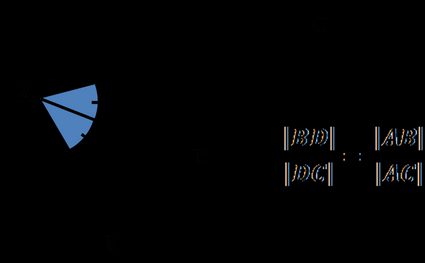
Angle bisector theorem states that:

An angle bisector of a triangle angle divides the opposite side into two segments that are proportional to the other two triangle sides.

Or, in other words:

The ratio of the B D ‾ \overline{BD} B D length to the D C ‾ \overline{DC} D C length is equal to the ratio of the length of side A B ‾ \overline{AB} A B to the length of side A C ‾ \overline{AC} A C :

Finding missing angles in triangles - example

OK, so let's practice what we just read. Assume we want to find the missing angles in our triangle. How to do that?

• Find out which formulas you need to use . In our example, we have two sides and one angle given. Choose angle and 2 sides option.
• Type in the given values . For example, we know that a = 9   i n a = 9\ \mathrm{in} a = 9   in , b = 14   i n b = 14\ \mathrm{in} b = 14   in , and α = 30 ° \alpha = 30\degree α = 30° . If you want to calculate it manually, use law of sines:
• From the theorem about sum of angles in a triangle, we calculate that γ = 180 ° − α − β = 180 ° − 30 ° − 51.06 ° = 98.94 ° \gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51.06\degree= 98.94\degree γ = 180° − α − β = 180° − 30° − 51.06° = 98.94° .
• The triangle angle calculator finds the missing angles in triangle . They are equal to the ones we calculated manually: β = 51.06 ° \beta = 51.06\degree β = 51.06° , γ = 98.94 ° \gamma = 98.94\degree γ = 98.94° ; additionally, the tool determined the last side length: c = 17.78   i n c = 17.78\ \mathrm{in} c = 17.78   in .

Reasoning similar to the one we applied in this calculator appears in other triangle calculations, for example the ones we use in the ASA triangle calculator and the SSA triangle calculator !

How do I find angles in a triangle?

To determine the missing angle(s) in a triangle, you can call upon the following math theorems:

• The fact that the sum of angles is a triangle is always 180° ;
• The law of cosines ; and
• The law of sines .

Which set of angles can form a triangle?

Every set of three angles that add up to 180° can form a triangle. This is the only restriction when it comes to building a triangle from a given set of angles.

Why can't a triangle have more than one obtuse angle?

This is because the sum of angles in a triangle is always equal to 180° , while an obtuse angle has more than 90° degrees. If you had two or more obtuse angles, their sum would exceed 180° and so they couldn't form a triangle. For the same reason, a triangle can't have more than one right angle!

How do I find angles of the 3 4 5 triangle?

Let's denote a = 5 , b = 4 , c = 3 .

• Write down the law of cosines 5² = 3² + 4² - 2×3×4×cos(α) . Rearrange it to find α , which is α = arccos(0) = 90° .
• You can repeat the above calculation to get the other two angles.
• Alternatively, as we know we have a right triangle, we have b/a = sin β and c/a = sin γ .
• Either way, we obtain β ≈ 53.13° and γ ≈ 36.87 .
• We quickly verify that the sum of angles we got equals 180° , as expected.

Angle selection

© Omni Calculator

Side length a

Side length b

Side length c

• Solving ...

Solving Triangles

In this tutorial, we’ll learn all about solving triangles. So let’s begin by looking at what it actually means to solve a triangle.

There are six values describing the six parts of a triangle — three sides and three internal angles.

Now, if we know any three of those six values, we can find the other three (with one exception that we’ll look at later). And that’s what solving triangles is all about.

To solve a triangle is to find its unknown (or required) side lengths and angles using what is known about the triangle.

Solving Triangles — Important Concepts

Before we dive into the different types of problems and examples and start solving them, here are the important concepts, formulas, and relations that are essential to being able to solve such problems.

So first things first. When naming sides and angles, a side is represented by the small case version of the letter for the opposite angle.

For example, the angle opposite to the side A B \hspace{0.2em} AB \hspace{0.2em} A B is angle C \hspace{0.2em} C \hspace{0.2em} C . So it (or its length) is represented by c \hspace{0.2em} c \hspace{0.2em} c .

Sum of Angles

The sum of the three internal angles of a triangle is 180 ° \hspace{0.2em} 180 \degree 180° .

Law of Cosines

The law of cosines gives the relationship between the side lengths of a triangle and the cosine of any of its angles. It says —

Re-framing the formula for other sides, we have

For cases where we need to find angles using the cosine rule, the three formulas can be rearranged as —

Law of Sines

The law of sines states that the ratio of side length to the sine of opposite angle is the same for all sides in a triangle.

When we find an angle using its sine value, there are two possibilities. The angle can be acute or obtuse (angle greater than 90 ° \hspace{0.2em} 90 \degree 90° ).

For example,

So which angle do we choose? Here are a couple of points to keep in mind.

A triangle can have a maximum of one obtuse angle. Otherwise, the sum would exceed 180 ° \hspace{0.2em} 180 \degree 180° .

The obtuse angle (if present) would be the angle opposite the largest side (itself being the largest angle).

If it sounds confusing, don’t worry. Wait till we get to the examples.

The Different Types

Depending on which three of the six values are known to us, the problems under the topic of solving triangles can be divided into five categories.

1. Side-Side-Side (SSS)

In this type, all three sides are known to us.

To solve, start by finding one angle using the cosine rule. Then find the two remaining angles using the sine rule.

2. Side-Angle-Side (SAS)

Here, two sides and the included angle (the angle contained between them) are known to us.

To solve, first find the third side using the law of cosines. Then find the two unknown angles using the law of sines.

3. Side-Side-Angle (SSA)

In this case, two sides and one angle (not included) are known.

(angle sum rule). Finally, find the missing side using the sine rule.

4. Angle-Side-Angle (ASA)

Here, two angles and the included side (the side shared by the two angles) are known to us.

To solve, start by finding the third side using the angle sum property. Then find the two unknown sides using the sine rule.

5. Angle-Angle-Side (AAS)

In this type, two angles and one side (not included) are known.

The steps to solve this are the same as those for the ASA type. The first step is to find the third angle using the angle sum property. Then you find the two unknown sides using the sine rule.

6. Angle-Angle-Angle (AAA)

In this case, the three angles are known to us.

You can’t solve this type. Here's why.

A triangle is not uniquely determined by its three angles. For the same three angles, you can have infinitely many triangles. They will have the same shape but different sizes ( similar triangles ).

For example, here are two triangles with the same internal angles (so similar by AA criteria) but with different size.

So how would one know which triangle it is without knowing at least one side-length?

Solving Triangles — Examples

Alright, now it’s time to use what we have learned so far and solve examples covering the different types discussed above.

The lengths of the three sides of a triangle are 6 \hspace{0.2em} 6 \hspace{0.2em} 6 , 3 \hspace{0.2em} 3 \hspace{0.2em} 3 , and 4 \hspace{0.2em} 4 \hspace{0.2em} 4 . Find the measures of its angles.

Step 0.  We start by drawing a rough sketch of the triangle and labeling the information given in the question. It’s not necessary but often makes things easier and helps avoid silly mistakes.

Step 1.  Use the Cosine Rule to find the largest angle

When we know all the side lengths, we can use the Cosine Rule to find any of the angles.

However, I strongly recommend you find the largest angle first — the angle opposite to the longest side. Why?

Because if there is an obtuse angle ( > 90 ° ) \hspace{0.2em} (>90 \degree) \hspace{0.2em} ( > 90° ) in the triangle, it has to be this angle. So once this is out of the way, we can use the sine rule to find the other angles without having to worry about the obtuse options.

Here the largest angle would be A \hspace{0.2em} A \hspace{0.2em} A . So using the formula for cos ⁡ A \hspace{0.2em} \cos A \hspace{0.2em} cos A , we have

Taking cos inverse on both sides.

Step 2.  Use the Sine Rule for one of the remaining angles

Now that we know the three sides and one angle, we can use the Sine Rule to find any of the remaining two angles. Let's go for B \hspace{0.2em} B \hspace{0.2em} B .

Taking sine inverse on both sides

Step 3.  Use the Angle Sum Property to find the third angle

And we have solved the triangle.

Note — We could have found the third angle ( C \hspace{0.2em} C \hspace{0.2em} C ) using the sine rule, as we did for angle B \hspace{0.2em} B \hspace{0.2em} B . I used the angles sum property just because the calculation was easier. You can also use one to find the angle and the other to validate your answer(s).

Two sides and the included angle in a triangle measure 12 \hspace{0.2em} 12 \hspace{0.2em} 12 , 14 \hspace{0.2em} 14 \hspace{0.2em} 14 , and 110 ° \hspace{0.2em} 110 \degree \hspace{0.2em} 110° . Solve the triangle for the missing side and angles.

Again, we start with a rough sketch for the problem.

Step 1.  Use the Cosine Rule to find the missing side

When we have two sides and the included angle, the law of cosines allows us to find the third side.

Applying the cosine rule for side b \hspace{0.2em} b \hspace{0.2em} b ,

Taking square root on both sides,

Step 2.  Use the Sine Rule for the remaining angles

At this point, we know three sides and one angle. So, we can find the unknown angles using the sine rule.

When using the sine rule to find an angle, go for the smaller angle (the one opposite the smaller side) if possible. Here’s why.

The smaller angle cannot be obtuse and so you can confidently accept the acute angle solution when taking the inverse of sine.

Here though, we already have an obtuse angle in the triangle. So, no matter which of the unknown angles we calculate first, we can safely ignore the obtuse options when taking sine inverse.

Alright, now lets split the equation and solve for C \hspace{0.2em} C \hspace{0.2em} C .

And finally, as we did in the last example, let's calculate the last angle using the angle sum property.

When it comes to problems of type SSA, it’s useful to divide them into two sub-types. Let me explain with an example of each type.

Solve the triangle below for the missing sides and angles.

In this example, we don’t need to draw anything as the question itself provides the figure.

Now the question gives us two sides and one angle (duh!) but —

The known angle is adjacent to the smaller of the two known sides and hence opposite to the larger side. That’s what makes this sub-type SsA (lowercase/small “s” is placed adjacent to “A”).

Step 1.  Use the Sine Rule to find the missing angle opposite to one of the known sides

Here, we know the sides b \hspace{0.2em} b \hspace{0.2em} b and c \hspace{0.2em} c \hspace{0.2em} c and the angle B \hspace{0.2em} B \hspace{0.2em} B . So we need to find angle C \hspace{0.2em} C \hspace{0.2em} C .

Applying the sine rule to B \hspace{0.2em} B \hspace{0.2em} B and C \hspace{0.2em} C \hspace{0.2em} C .

We know C \hspace{0.2em} C \hspace{0.2em} C is acute because the opposite side, c \hspace{0.2em} c \hspace{0.2em} c , is certainly not the largest ( c < b ) \hspace{0.2em} (c < b) \hspace{0.2em} ( c < b ) .

Step 2.  Find the third angle using the angle sum property

Step 3.  Find the missing side using the sine rule

That’s it.

In △ A B C \hspace{0.2em} \triangle ABC \hspace{0.2em} △ A BC , b = 15 \hspace{0.2em} b = 15 \hspace{0.2em} b = 15 , c = 21 \hspace{0.2em} c = 21 \hspace{0.2em} c = 21 , and B = 42 ° \hspace{0.2em} B = 42 \degree \hspace{0.2em} B = 42° . Solve the triangle.

Here’s the drawing to get started.

This is an example of the other sub-type where the known angle is adjacent to the larger of the two known sides and hence opposite to the smaller side. That’s what makes this sub-type sSA (uppercase “S” is placed adjacent to “A”).

This case is often termed as the “ ambiguous case ” because, as you’ll see, it has two potential solutions. And unless we have more information about the problem, we can’t pick one over the other. So both solutions must be worked out.

Unlike in the last example, here, we need to consider both acute and obtuse values for C \hspace{0.2em} C C . That’s because side c     ( A B ) \hspace{0.2em} c \, \, (AB) \hspace{0.2em} c ( A B ) could be the largest side. It is larger than b \hspace{0.2em} b \hspace{0.2em} b , and we don’t know a \hspace{0.2em} a \hspace{0.2em} a yet.

Acute Solution for C \hspace{0.2em} C \hspace{0.2em} C

Obtuse Solution for C \hspace{0.2em} C \hspace{0.2em} C

Note — When using the sine rule, you can get the obtuse solution by subtracting the acute solution from 180 ° \hspace{0.2em} 180 \degree 180° .

Next, we'll need to work out the remainder of the solution for each of the two cases.

First, let's go ahead assuming C \hspace{0.2em} C \hspace{0.2em} C is acute.

Step 4.  Repeat steps 2 and 3 assuming C \hspace{0.2em} C \hspace{0.2em} C is obtuse.

Again, first, we find angle A \hspace{0.2em} A \hspace{0.2em} A .

And then side a \hspace{0.2em} a \hspace{0.2em} a

Great, we have found all the missing values for both possible solutions. To make things clearer, here are their drawings.

Note - Before we move ahead, I want to make it clear you don’t always have to worry about multiple solutions. Of the six cases we discuss in this tutorial, this is the only one of that kind.

Solve the triangle below.

Step 1.  Find the third angle using the angle sum property

Step 2.  Find the missing side using the sine rule

You know what to do now — split it into two equations and solve for b \hspace{0.2em} b \hspace{0.2em} b and c \hspace{0.2em} c \hspace{0.2em} c .

Solving for b \hspace{0.2em} b \hspace{0.2em} b

Solving for c \hspace{0.2em} c \hspace{0.2em} c

Triangle solved.

In △ A B C \hspace{0.2em} \triangle ABC \hspace{0.2em} △ A BC , c = 14 \hspace{0.2em} c = 14 \hspace{0.2em} c = 14 , B = 45 ° \hspace{0.2em} B = 45 \degree \hspace{0.2em} B = 45° , and C = 55 ° \hspace{0.2em} C = 55 \degree \hspace{0.2em} C = 55° . Solve the triangle.

Step 1.  Here, we know two angles. So, we find the third angle using the angle sum property

Step 2.  Find the missing sides using the sine rule

Solving for a \hspace{0.2em} a \hspace{0.2em} a

And with that, we come to the end of this tutorial on solving triangles. Until next time.

We use cookies to provide and improve our services. By using the site you agree to our use of cookies. Learn more

Find the missing angle in a triangle

In these lessons we look into finding the measure of an angle in a triangle.

Related Pages Angles Of A Triangle More Lessons for Grade 6

Worksheets to find the missing angle in a triangle Missing Angles in a Triangle I Missing Angles in a Triangle II

The following diagrams show some triangles with missing interior and exterior angles. Scroll down the page for step by step solutions on how to find the missing angles in triangles.

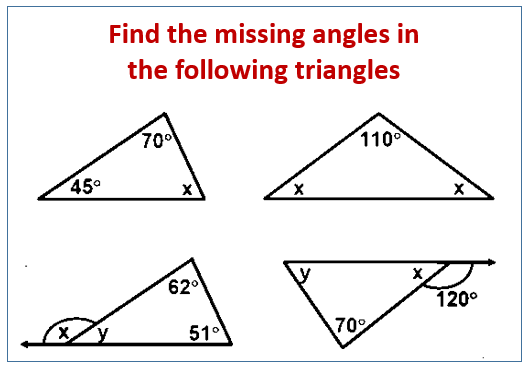
Finding the Missing Angles of a Triangle How to find the missing interior and exterior angles of a triangle?

We can use the property that the angles of a triangle add up to 180 degrees. Step 1: Find the given angles Step 2: Subtract the given angles from 180 to get the missing angle.

Angles of Triangles Add Up To 180 Degrees Ex: Could a triangle have the given angle measures? a) 115, 35, 30 b) 45, 45, 60

Angles of Triangles Add Up To 180 Degrees Since all three angles add up to 180 degrees, you can find the missing angle by subtraction.

Angles of Triangles Add Up To 180 Degrees Find two missing angles that are equal.

How to Find the Missing Angle in a Triangle?

How to find a missing angle in a triangle?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Triangle Solving Practice

Practice solving triangles .

You only need to know:

• Angles Add to 180°
• The Law of Sines
• The Law of Cosines

Try to solve each triangle yourself first, using pen and paper.

Then use the buttons to solve it step-by-step (more Instructions below).

Instructions

• Look at the triangle and decide whether you need to find another angle using 180°, or use the sine rule, or the cosine rule.  Click your choice .
• The formula you chose appears, now click on the variable you want to find.
• The calculation is done for you.
• Click again for other rules until you have solved the triangle.

Note: answers are rounded to 1 decimal place.

What Does "AAS", "ASA" etc Mean?

It means which sides or angles we already know:

Reset password New user? Sign up

Existing user? Log in

Already have an account? Log in here.

• Christopher Williams
• Sharky Kesa
• Niranjan Khanderia
• Jordan Calmes
• Anuj Shikarkhane
• Gene Keun Chung
• Mahindra Jain
• Andrew Ellinor
• A Former Brilliant Member

Triangles are polygons (shapes) with three sides and three angles , which can be formed by connecting any three points in a plane. They are one of the first shapes studied in geometry .

Triangles are particularly important because arbitrary polygons (with 4, 5, 6, or \(n\) sides) can be decomposed into triangles . Thus, understanding the basic properties of triangles allows for deeper study of these larger polygons as well. Interestingly, the triangle is the only rigid polygon formed out of straight line segments, meaning that if the three lengths of the sides are given, the measurements correspond to a unique triangle. Because of this, it is often possible, given some information about a triangle (e.g. some side lengths and some angles), to determine additional facts about the triangle.

An equilateral triangle, a right triangle, and a scalene triangle

Sum of Angles in a Triangle

Triangle inequality, classifying triangles, area of triangles, exterior angles of triangles, problem solving with triangles.

If \(ABC\) is a triangle, then \(\angle ABC + \angle BCA + \angle CAB = 180^\circ.\) In other words, the sum of the \(3\) internal angles in any triangle is \(180^\circ.\)

Draw line \(DE\) that is parallel to \(AB\) and passes through \(C\) as in the above figure. Since \( DE \parallel AB \), applying the principle of alternate interior angles shows that \( \angle DCA = \angle CAB \) and \( \angle BCE = \angle CBA.\) Since angles in a line sum up to 180 degrees, \( \angle DCA + \angle ACB + \angle BCE = 180^ \circ \). Thus, we conclude that \( \angle CAB + \angle ACB + \angle CBA = \angle DCA + \angle ACB + \angle BCE = 180^ \circ \). \(_\square\)

Main article: Triangle Inequality

Triangles have the property that the sum of any two sides of the triangle is always strictly greater than the third side. This property, known as the triangle inequality , is explored in the wiki linked above.

Main article: Classification of Triangles

Triangles can be classified into different categories based on their sides and angles. For example, a triangle with one angle of measure \(90^\circ\) is known as a right triangle, while a triangle with sides of all equal length is known as an equilateral triangle. These classifications and many others are explored in the wiki linked above.

Main article: Area of a Triangle

When determining the area of a triangle, note that a triangle can be thought of as half of a parallelogram . The following picture should make this point clear:

Because the area of a parallelogram is equal to the product of its base and height, the area of a triangle is simply half of that area.

The area of a triangle is \(A = \frac{bh}{2}\), where \(b\) is the length of the base and \(h\) is the height.

What is the area of a triangle with base 10 and height 6? The area of this triangle is \(\frac{10 \times 6}{2} = 30.\) \(_\square\)

Nihar and Andrew are trying to find the area of \(\triangle ABC\) using the formula

\[\dfrac{1}{2} \times \text{base} \times \text{height}. \]

Nihar mistakenly multiplies base \(AB\) by the height from \(A\) \((\)instead of \(C).\) He gets a value of 14.

Andrew mistakenly multiplies base \(BC\) by the height from \(C\) \((\)instead of \(A).\) He gets a value of 56.

Find the actual area of triangle \(\triangle ABC\).

For more advanced methods of finding the area of a triangle, such as Heron's formula , see the wiki linked at the top of this section.

The measure of an exterior angle of a triangle is the sum of its two remote interior angles. Remote interior angles are the interior angles of a triangle that are opposite to the exterior angle under consideration.

For regular polygons , the formula to find the exterior angle of a polygon is \(\frac{360^\circ}{n},\) where \(n\) is the number of sides.

Prove that \(\angle ABC+\angle CAB=\angle DCA. \) ExteriorAngle ANSWER From the property of triangles-angle sum , the sum of measures of all angles in a triangle is \(180^\circ\). So, in \(\triangle ABC\), it follows that \( \angle ABC + \angle BCA + \angle CAB = 180^\circ \). Since \( \angle BCA \) and \( \angle DCA \) form a straight line, \( \angle BCA + \angle DCA = 180^\circ, \) It follows that both sets of angles are equal to \( 180^\circ: \) \[ \angle ABC + \angle BCA + \angle CAB = \angle BCA + \angle DCA.\] Therefore, \[ \angle ABC + \angle CAB = \angle DCA. \ _\square \]

Triangle \(ABC\) has the property that \(\angle A+\angle B= \angle C\). Find the measure of \(\angle C\) in degrees.

Mary drew a triangle on the board. What is the sum of all interior angles in a triangle?

Interested in learning more about triangles? Check out these pages:

• Congruent and Similar Triangles
• Pythagorean Theorem
• Triangles - Calculating Area

Problem Loading...

Note Loading...

Set Loading...

Angles on a straight line add to 180°

Example 1: Find the size of angle a

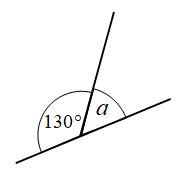
Angles on a straight line add to 180° a + 130° = 180° a = 50°

Example 2: Find the size of angle b

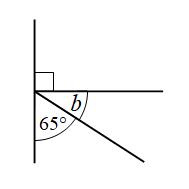
Angles on a straight line add to 180° b + 90° + 65° = 180° b + 155° = 180° b = 25°

Find the size of angle c:

Find the size of angle d:

Angles around a point add to 360°

Example 3: Find the size of angle e

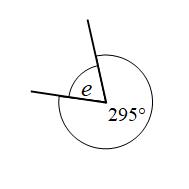
Angles around a point add to 360° e + 295° = 360° e = 65°

Example 4: Find the size of angle f

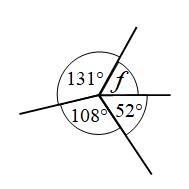
Angles around a point add to 360° f + 131° + 108° + 52° = 360° f + 291° = 360° f = 69°

Find the size of angle g:

Triangles Calculator

Calculate area, perimeter, sides and angles for triangles step-by-step.

• Basic (Linear)
• Biquadratic
• Logarithmic
• Exponential
• Solve For x
• Scientific Calculator
• Scientific Notation Arithmetics
• Complex Numbers
• Cartesian to Polar
• Polar to Cartesian
• System of Inequalities
• Partial Fractions
• Periodicity
• Y Intercept
• X Intercepts
• Point Slope Form
• Step Functions
• Arithmetics
• Start Point
• Area & Perimeter
• Sides & Angles

Law of Sines

Law of cosines.

• Width & Length
• Volume & Surface
• Edges & Diagonal
• Volume & Radius
• Surface Area
• Radius & Diameter
• Volume & Height
• Circumference
• Eccentricity
• Trigonometric Equations
• Evaluate Functions

Equilateral

Isosceles Triangle

Right Angled

triangles-calculator

Related Symbolab blog posts

Please add a message.

Message received. Thanks for the feedback.

Triangle Calculator

Enter the values of any two angles and any one side of a triangle below which you want to solve for remaining angle and sides.

Triangle calculator finds the values of remaining sides and angles by using Sine Law.

Sine law states that

a sin A = b sin B = c sin C

Cosine law states that-

a 2 = b 2 + c 2 - 2 b c . cos ( A ) b 2 = a 2 + c 2 - 2 a c . cos ( B ) c 2 = a 2 + b 2 - 2 a b . cos ( C )

Click the blue arrow to submit. Choose "Solve the Triangle" from the topic selector and click to see the result in our Trigonometry Calculator!

Solve the Triangle

Popular Problems-

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Choose Your Test

Sat / act prep online guides and tips, triangles on act math: geometry guide and practice problems.

If you thought the ACT was a big fan of circles , then brace yourself for its absolutely shameless love of triangles. In one breath, you may be expected to find the various dimensions of an obtuse triangle, and the next, an isosceles right triangle. ACT triangle problems will be as numerous as they are varied, so make sure you familiarize yourself with all the different types before test day.

This will be your complete guide to ACT triangles --the types of triangles that will show up on the ACT, the formulas you’ll need to know to solve them, and the strategies you’ll need to apply when approaching a triangle question. We’ll also break down real ACT math problems and give you the walk-throughs on how to most efficiently and effectively tackle any and all triangle problems you come up against.

What Are Triangles?

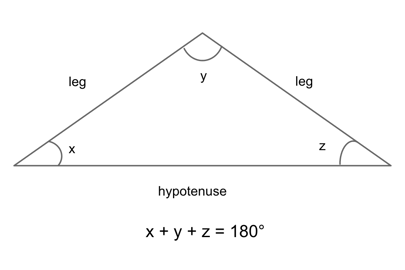
Before we go through how to solve a triangle problem, let’s discuss the basics. A triangle is a flat figure made up of three straight lines that connect together at three angles. The sum of these angles is 180°.

Each of the three sides of a triangle is called a “leg” of the triangle, and the largest (longest) leg is called the “hypotenuse.” The angle opposite the hypotenuse will always be the largest of the three angles.

The sum of any two legs of a triangle must always be greater than the measure of the third side. Why? Because when the sum of two lines is smaller than the measure a third line, they cannot all connect to form a triangle.

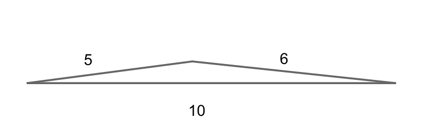
Triangles that have legs which sum only slightly more than the hypotenuse are quite long and skinny, but they still make the “bump” of a triangle because they combine to be longer than the third side.

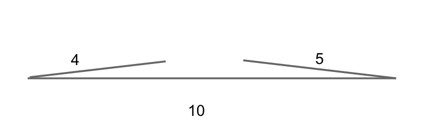
But if the legs are too short, they will never meet, no matter how shallow the angle.

And if the lines are the exact length of the hypotenuse, then they will flatten to a perfectly straight line, overlapping the hypotenuse precisely.

Let's look at an example ACT problem of this kind:

A triangle has side lengths of 6 inches and 9 inches. If the third side is an integer, what is the least possible perimeter, in inches, of the triangle?

We know, based on our rules for the side lengths of triangles, that the sum of two sides must be greater than the third. Because we are trying to find the smallest perimeter, we must find our missing side by taking the difference of our two leg lengths:

$9 - 6 = 3$

Considering the sum of two legs must be greater than the third side, our missing side must be greater than 3. (Why? Because $6 + 3 = 9$ and we need the sum to be larger than 9.)

If our missing side is an integer value (which we are told is true), and we are trying to find the minimum perimeter value, then our missing side must be the smallest integer greater than 3.

Which means that our missing side is 4.

To find our perimeter, then, we must add all our sides together:

$4 + 6 + 9 = 19$

Our final answer is D , 19.

(Note: always pay attention to the exact question you’re being asked and don’t get tricked by bait answers! If you were going too quickly through the test, you might have been tempted to select answer choice A, 4, which was the value of the missing side length. But, since we were asked to find the perimeter , this would have been the wrong answer.)

Ready to enter the realm of special triangles (and become insanely awesome)?

Special Triangles

There are several different kinds of special triangles, all of which commonly appear on the ACT.

In this section, we will define and describe all the different kinds of triangles you’ll see on the test. In the next section, we will go through all the formulas you’ll need to know for your ACT triangle problems, as well as how to use them.

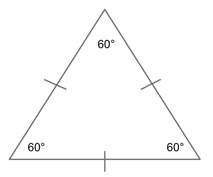
Equilateral Triangles

An equilateral triangle is a triangle that has three equal legs and three equal angles. Though the leg measurements can be anything (so long as they are all equal), the angle measurements must all equal 60°. Why? Because a triangle’s angles must always total 180°, and $180/3 = 60$.

Isosceles Triangles

An isosceles triangle is a triangle in which two sides and two angles are equal.

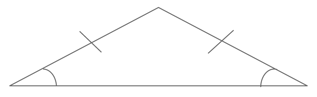
The sides opposite equal angles will always be equal and the angles opposite equal sides will always be equal. This knowledge will often lead you to the correct answers for many ACT questions in which it seems you are given very little information.

(We will go through how to solve this problem later in the guide, but for now, note how it seems as if you are not given enough information. But, if you remember that angles opposite equal lines are also equal, then you’ll see that you now have exactly enough to solve the problem)

Right Triangles

A right triangle is a triangle in which one of the angles measures 90° (90° is a right angle). This means that the sum of the other two angles must be 90° as well, since a triangle’s angles always add up to 90°.

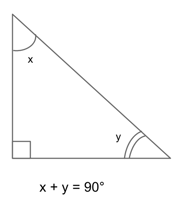
The leg opposite the 90° angle will always be the triangle’s hypotenuse. This is due to the fact that the 90° angle will always be the largest angle in a right triangle. (Why? Because two 90° angles would make a straight line , not a triangle.)

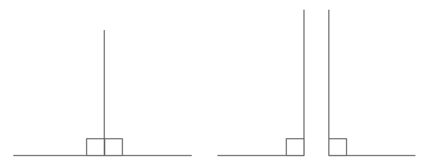
Special Right Triangles

There are many different kinds of right triangle and some are considered “special.” These are triangles that have set angles or side lengths and formulas to correspond with them. Understanding these types of triangles (and their formulas) will save you a significant amount of time as you go through your test.

We will go through the formulas that correspond with these types of triangles in the next section, but for now, let’s go through their definitions.

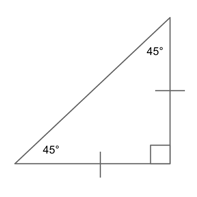
Isosceles Right Triangle

An isosceles right triangle is just what it sounds like--a right triangle in which two sides and two angles are equal.

Though the side measurements may change, an isosceles triangle will always have one 90° angle and two 45° angles. (Why? Because a right triangle has to have one 90° angle by definition and the other two angles must add up to 90°. So $90/2 = 45$.)

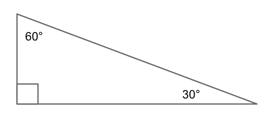
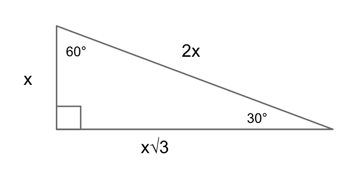
30-60-90 Triangles

A 30-60-90 triangle is a special right triangle defined by its angles. It is a right triangle due to its 90° angle, and the other two angles must be 30° and 60°.

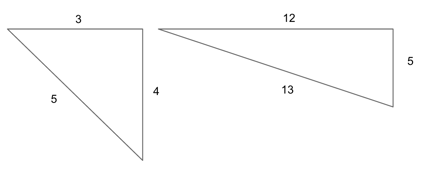
3-4-5, and 5-12-13 Right Triangles

3-4-5 and 5-12-13 triangles are special right triangles defined by their side lengths. The numbers 3-4-5 and 5-12-13 describe the lengths of the triangle’s legs, meaning that, when you have a right triangle with two leg lengths of 4 and 5, then you automatically know that the third leg equals 3. Any consistent multiples of these numbers will also work the same way. So a right triangle could have leg lengths of:

3(1)-4(1)-5(1) => 3-4-5

3(2)-4(2)-5(2) => 6-8-10

3(3)-4(3)-5(3) => 9-12-15

These are considered special right triangles because all their sides are integers.

Now it's triangle formula time!

Triangle Formulas

Now that you know what all your triangles will look like, let’s go through how to find missing variables and information about them.

You will not be given any formulas on the ACT, so you must know all of these formulas by heart. (For more on the formulas you’ll need for the ACT math section, check out our guide to the 31 formulas you must know before test day .)  

But beyond memorizing your formulas, you also must take care to understand them--how they work and when. All the rote memorization in the world won’t help you if you don’t know when or how to apply them when solving your problems.

All Triangles

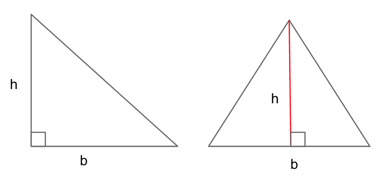
$a = {1/2}bh$

$b$ is the base of the triangle, which is the length of any one of the triangle’s legs.

$h$ is the height of a triangle, found by drawing a straight line (at a 90° angle) from the base of the triangle to the opposite angle from the base.

This means that, in a right triangle, the height is the length of the leg that meets at a 90° angle to the base. In a non-right triangle, you must create a new line for your height.

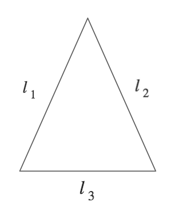
$p = l_1 + l_2 + l_3$

Just like with any other kind of plane geometry figure, the perimeter of a triangle is the sum of its outer sides (the triangle’s three legs).

Some triangle formulas apply specifically to right triangles, so let's take a look.

Pythagorean Theorem

$a^2 + b^2 = c^2$

The Pythagorean theorem allows you to find the side lengths of a right triangle by using the lengths of its other sides. $a$ and $b$ signify the shorter legs of the triangle, while $c$ is always the leg opposite the 90° angle (the hypotenuse).

According to the Pythagorean theorem, $a^2 + b^2 = c^2$. We know that the side with $y$ meters must be our hypotenuse, as it is opposite the 90 degree angle. This means that:

$a^2 + b^2 = c^2$ 

$4^2 + x^2 = y^2$

Now, we need to find $y$ in terms of $x$, which means we need to isolate our $y$. 

$16 + x^2 = y^2$ 

$y = √{16 + x^2}$

Our final answer is E , $√{x^2 + 16}$

3-4-5 and 5-12-13 triangles (and their multiples) are special because you do not need to work through the pythagorean theorem in order to find the side measures of the third length. Remember, if two sides of a right triangle are 12 and 15, then you automatically know the third side is 9 (because $3(3)-4(3)-5(3) = 9-12-15$).

Though we can find the length of BC using the Pythagorean theorem, we can also simply know that it is 5. (Why? Because it is the hypotenuse of a right triangle with leg lengths of 3 and 4). 

Now, we can set up a proportion to find the measure of side AE. The length of AE to its hypotenuse will be in proportion to the length of BD to its hypotenuse. 

${AE}/20 = 3/5$

Our final answer is B , 12.

$x, x, x√2$

Though you can find the missing side lengths of an isosceles triangle using the Pythagorean theorem, you can also take a shortcut and say that the equal side lengths are $x$ and the hypotenuse is $x√2$.

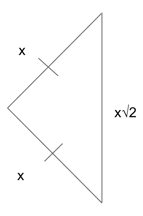
Why does this work? Let’s look at an isosceles right triangle problem.

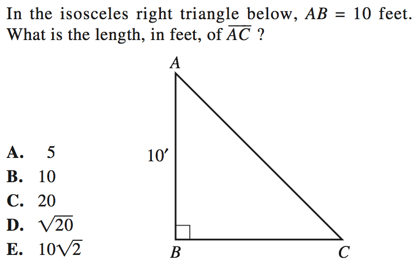
It is given to us that one side length equals 10, so we know the second leg must also equal 10 (because the two legs are equal in an isosceles triangle). We can also find the hypotenuse using the Pythagorean theorem because it is a right triangle. So:

$10^2 + 10^2 = c^2$

$100 + 100 = c^2$

$200 = c^2$

$c = √100 * √2$ (Why were we able to split up our root this way? Check out our guide to ACT advanced integers and its section on roots if this process is unfamiliar to you.)

So, we are left with side lengths of 10, 10, and 10√2. Or, in other words, our side lengths are $x, x$, and $x√2$.

So our final answer is E , $10√2$

30-60-90 Triangle

$x, x√3, 2x$

Just like with an isosceles right triangle, a 30-60-90 triangle has side lengths that are dictated by a set of rules. 

Again, you can find these lengths with the Pythagorean theorem, but you can also always find them using the rule: $x, x√3, 2x$, where $x$ is the side opposite 30°, $x√3$ is the side opposite 60°, and $2x$ is the side opposite 90°.

Make a note now of any formulas that are unfamiliar to you. You will need to know them by test day, so a little practice and organization now will go a long way to keeping them straight in your head.

Typical Triangle Questions

Most triangle question on the ACT will involve a diagram, though a rare few will be purely word problems. Let’s look at some of the standard types of question in each category.

Word Problems

Most triangle word problems are fairly simplistic once you draw them out. In fact, often times, the very reason why they give you the problem as a word problem instead of providing you with a diagram is because the test-makers thought the problem would be too easy to solve with a picture.

Whenever possible, draw your own diagram when you are given a triangle problem without one. It won’t take you long and it’ll be much simpler for you to visualize the question.

This should be a simple figure, but it never hurts to quickly sketch it out in order to keep all our parts in order.

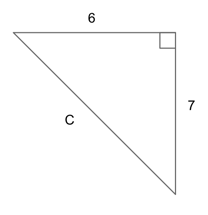
We are told that this is a right triangle and we need to find one missing side length, so we will need to use the Pythagorean theorem.

Using our given side lengths for $a$ and $b$, we have:

$6^2 + 7^2 = c^2$

$36 + 49 = c^s$

Our final answer is G , $√85$

Diagram Problems

There are several different kinds of triangle problems that involve diagrams. Let’s break them into categories and discuss the strategies for each.

Diagram Type 1 - Finding Missing Values

Most triangle problems will fall into this category--you will be asked to find a missing angle, an area, a perimeter, or a side length (among other things) based on given information.

Some of these questions will be more complicated than others, but the ACT will always provide you will enough information to solve a problem, so it’s up to you to put the clues together.

Let’s walk through some real ACT math examples of this type:

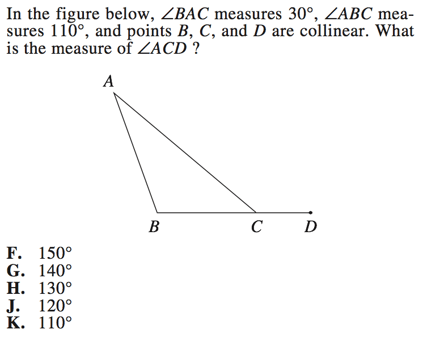
First, let us fill in our given information so that we don't lose track of which angles measure what.

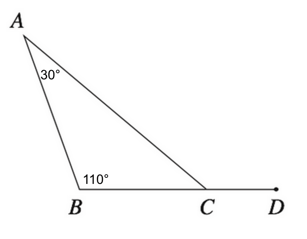
We know that the interior angles in a triangle sum up to 180 degrees, so we can find ACB by subtracting our givens from 180. 

$180 - 30 - 110$

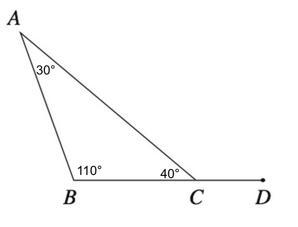
We also know that any straight line will measure 180 degrees. BCD are collinear, which means that they lie on a straight line. We can therefore find angle ACD by subtracting our ACB measure from 180.

Our final answer is G , 140°.

Similar triangles are in proportion with one another, so we can find the side lengths for triangle BAC by setting up proportions with triangle LKM. 

${BA}/{AC} = {LK}/{KM}$

${BA}/3 = 12.5/7.5$

$7.5BA = 37.5$

And our second proportion will follow the same model. 

${AC}/{BC} = {KM}/{LM}$

$3/{BC} = 7.5/15$

$7.5BC = 45$

Now, we have all the side measures for triangle BAC, which means we can find its perimeter. 

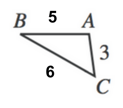
$5 + 3 + 6$

Our final answer is B , 14. 

Diagram Type 2 -  Ratios and (In)Equalities

These kinds of questions will generally ask you to either find the ratios between parts of different triangles or will ask you whether or not certain sides or angles of triangles are equal or unequal.

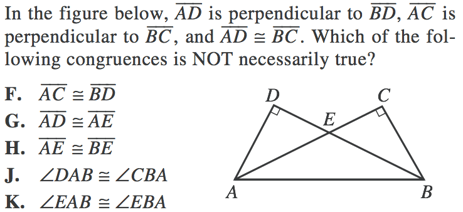
We are told that AD is equal to BC, which means that their corresponding angles will also be equal. This means that angles CAB and DBA are equal (which consequently means that angles EAB and EBA are equal). We can therefore eliminate answer choice K. 

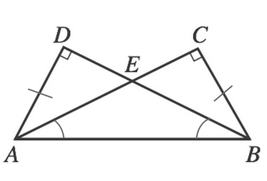
Now, if angles CAB and DBA are equal, then angles CBA and DAB must ALSO be equal. Why? Well we know that each triangle has a 90 degree angle and one angle to equal to some unknown measurement (which we could call $x$). This means that the third, remaining, angle (let's call it $y$) must ALSO be the same for each triangle. 

Each triangle would then be made up of:

$180 = 90 + x + y$

This means that we can eliminate answer choice J.

By that same reckoning, if angle DAB = angle CBA, then the legs opposite those angles must also be equal. This means that AC = BD, which means that answer choice F can be eliminated.

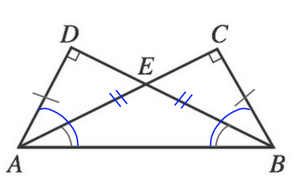
Because AD and CB are equal and both are part of a triangle with a hypotenuse of AB, legs CA and DB will cross in a manner that makes each half of the leg equal to the corresponding half of the leg of the other triangle. In other words, AE = EB and DE = EC. This means we can eliminate answer choice H. 

The only answer choice we are left with is G. AD CANNOT equal AE. Why? AD is the leg of triangle ADE, while AE is the hypotenuse of that same triangle. From our definitions, we know that the hypotenuse must always be the longest side of the triangle and so it cannot be equal to one of the legs. 

Our final answer is G. 

Diagram Type 3 -  Multi-Shape or Shapes Within Shapes

As you can see from earlier examples, some of the triangle problems on the ACT will involve multiple triangles (or other geometric shapes) combined together. This technique for presenting you problems is designed to challenge your understanding of lines and angles as well as triangles.

For these types of problems, you must use the information you are given and solve for more information down the line until you find exactly what you’re looking for. It’s essentially a domino effect of problem solving.

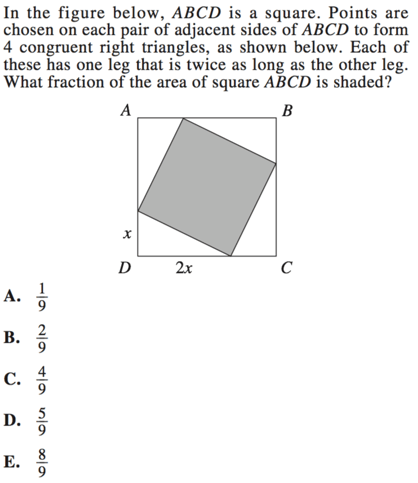
Because this problem uses variables, the simplest way to solve it is by  plugging in our own numbers . So let us do so. 

We are told that each unshaded triangle is a congruent right triangle. Because variables can be difficult to work with, let us replace $x$ with 4. (Why 4? Why not!)

This means that each triangle has one leg that measures 4 and one leg that measures $2(4) = 8$. 

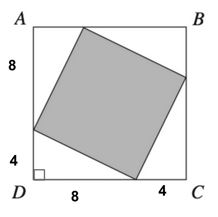
Now, we can find the length of one side of the square ABCD by adding our values together. 

Each side of the square ABCD is equal to 12. Now we can find the total area by squaring this side measure, so:

The total area for ABCD is 144.

Now, because each unshaded triangle is a right triangle, we can find the side measures for the shaded square using the Pythagorean theorem.

$4^2 + 8^2 = c^2$

$16 + 64 = c^2$

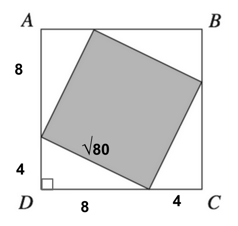
Since this is the measure of one side of the shaded square, we can now find the area for the shaded square by squaring this number. So:

Now, we must simply divide our shaded square by our unshaded square, ABCD, in order to determine what fraction it is of the larger square. 

$80 ÷ 16 = 5$ and $144 ÷ 16 = 9$

Our final answer is D , $5/9$

Life lessons and triangle strategies--win-win!

Strategies for Solving a Triangle Question

Because there are so many different kinds of triangle problems, it is difficult to break down one exact path for problem solving them.

That said, your greatest assets and strategies when solving triangle problems will be to follow these four steps:

#1: Write down your formulas

Because you are not given any formulas, you must keep them in your head and in your heart. The good news is that more you practice, the better you’ll be at rattling off triangle areas or side lengths of 30-60-90 triangles or anything else you’ll need.

But if you feel like you’ll forget your formulas as you go through your test, take a few seconds and write them down before you start solving your questions. Once you do, they will be there indelibly for you to work from for the rest of the math section, and you won’t have to worry about forgetting them.

#2: Use your formulas (and take your short-cuts)

Once you’re sure that you’ve remembered your formulas, using them is the absolute most crucial step for any triangle problem. And, considering that most of your formulas essentially act as short-cuts (why bother solving with the Pythagorean theorem when you know that the legs of a 30-60-90 triangle are $x, x√3, 2x$?), you will save yourself a great deal of time and energy when you can keep your formulas on hand and in order.

#3: When working with multi-shapes, break it into small steps

Remember that dealing with a multi-shape triangle problem is like working with dominoes. Each successive piece of information makes way for finding the next piece of information.

Don’t get intimidated that you don’t have enough information or that there are too many shapes or lines to deal with. You will always have enough data to go on--just focus on finding one shape and one piece of information at a time, and the dominoes will fall into place.

#4: Draw it out

Draw your own diagrams if you are given none. Draw on top of your diagrams when you are given pictures. Write in your givens and all the measurements you find along the way to your missing variable (or variables), mark congruent lines and angles.

The more you can clarify your diagrams, the less likely you’ll be to make careless errors in misplacing or confusing your numbers and equalities.

Ready to put your knowledge to the test?

Test Your Knowledge

Now let's test your triangle knowledge against some more real ACT math problems.

Answers: B, F, E, H

Answer Explanations:

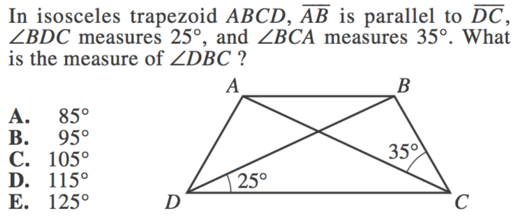
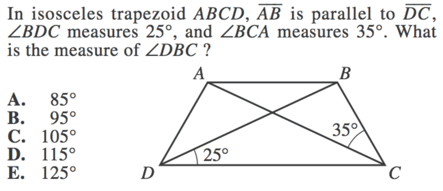
1)  Because we are told that this is an isosceles trapezoid, we know that each non-parallel side must be equal. This means that the angles that capture these sides (angles BDC and ACD) must also be equal. 

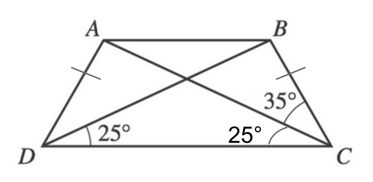
We also know that the interior degrees of a triangle will always sum 180 degrees, so we can find the measure of DXC by subtracting our two known angles from 180. 

$180 - 25 - 25$

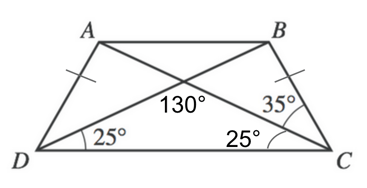
Now, DB is a straight line, which means that the angles that make the line must total 180 degrees.  This means we can find angle BXC by subtracting our known angle from 180. 

$180 - 130$

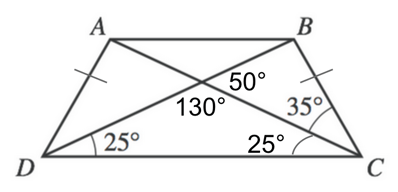
Finally, we again know that a triangle's interior angles will sum to 180, so we can find DBC by subtracting our known angles from 180. 

$180 - 50 - 35$

Our final answer is B , 95°.

2)  We know from our triangle definitions that the larger the side opposite an angle, the larger the angle will be. (If you ever feel unsure about the relationships between angles and sides of a triangle, you can also consult your rules and definitions of trigonometry .)

So if we drew in some random side measurements for XZ and YZ (so long as they follow the rule that XZ > YZ), we can see clearly that angle Y will be greater than angle X. 

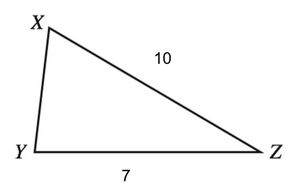
Our final answer is F, angle X < angle Y. 

3)  We are told that the triangle is a hypotenuse right triangle, which means that we can use our shortcuts to find the other two side lengths. 

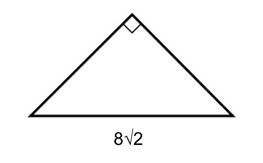
We know that an isosceles right triangle has side lengths of $x, x$, and $x√2$. Since we already know that the hypotenuse is $8√2$, we can say that the other two sides both measure 8. 

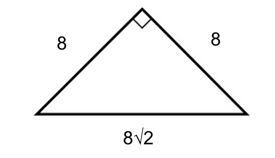
Now, we can add together the legs to find the perimeter. 

$8 + 8 + 8√2$

Our final answer is E, $16 + 8√2$

4)  Before we do anything else, let us fill in our given information. 

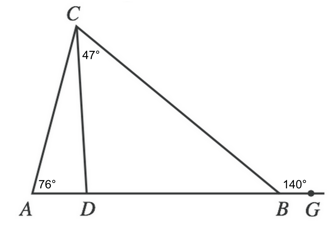
Now, we can know the triangles and the exterior angle are all collinear, which means that the angles that create the line will sum to 180°. This means we can find angle CBD by subtracting our exterior angle from 180. 

$180 - 140$

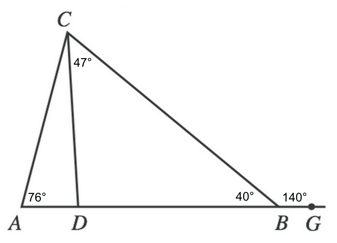
Now that we have two interior angle measures in triangle DCB, we can find the measure of the third (because the interior angles in a triangle will always add up to 180).

$180 - 40 - 47$

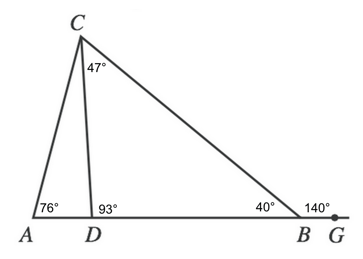
[Note: you may notice that the sum of the two angles not touching the exterior angle sum up to equal the exterior angle--$47 + 93 = 140$. This is not a coincidence. It will always be the case that the two non-connected angles will sum to equal the exterior angle of any type of triangle.)

Now we again have two angles that create a straight line, which means that we can find the measure of angle CDA by subtracting our known angle from 180°. 

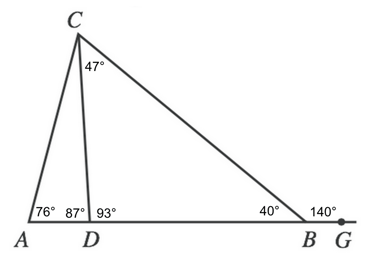
And finally, CAD forms a triangle, which means that its interior angles will sum to equal 180. We can find angle ACD by subtracting our two known values from 180°. 

$180 - 76 - 87$

Our final answer is H, 17°. 

Aw, yea. You've earned that nap.

The Take-Aways

Whether it be a trigonometry problem or a geometry problem, you’ll see triangles several times on any given ACT. Though most triangle problems are fairly straight forward, you’ll need to know the basic building blocks of triangles and geometry in order to understand how to solve them.

Know your definitions, memorize your formulas, and do your best to keep a clear head as you go through your test. And, as always, practice, practice, practice! The more experience you get in solving the variety of triangle questions the ACT can think to put in front of you, the better off you’ll be.

What’s Next?

Whoo! You took on triangles and won (give yourself a round of applause)! In the mood for more geometry? Hop on over to our guides on ACT circles , polygons , and solid geometry and round off all your geometry studies in one go.

Not sure what topic to tackle next? Make sure you've got a clear idea of all the math topics you'll be tested on and check out all of our ACT math guides for reference and practice. Each guide has definitions, formulas, and real ACT practice questions and will break down the solving process step-by-step. 

Been procrastinating? Check out our guide on how to take back your study time and beat back those procrastination demons.

Looking to get a perfect score? Our guide to getting a 36 on the ACT math (written by a perfect-scorer!) will help get you where you need to go.

Want to improve your ACT score by 4 points?

Check out our best-in-class online ACT prep program . We guarantee your money back if you don't improve your ACT score by 4 points or more.

Our program is entirely online, and it customizes what you study to your strengths and weaknesses . If you liked this Math lesson, you'll love our program. Along with more detailed lessons, you'll get thousands of practice problems organized by individual skills so you learn most effectively. We'll also give you a step-by-step program to follow so you'll never be confused about what to study next.

Check out our 5-day free trial:

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.

Ask a Question Below

Have any questions about this article or other topics? Ask below and we'll reply!

Improve With Our Famous Guides

• For All Students

The 5 Strategies You Must Be Using to Improve 160+ SAT Points

How to Get a Perfect 1600, by a Perfect Scorer

Series: How to Get 800 on Each SAT Section:

Score 800 on SAT Math

Score 800 on SAT Reading

Score 800 on SAT Writing

Series: How to Get to 600 on Each SAT Section:

Score 600 on SAT Math

Score 600 on SAT Reading

Score 600 on SAT Writing

Free Complete Official SAT Practice Tests

What SAT Target Score Should You Be Aiming For?

15 Strategies to Improve Your SAT Essay

The 5 Strategies You Must Be Using to Improve 4+ ACT Points

How to Get a Perfect 36 ACT, by a Perfect Scorer

Series: How to Get 36 on Each ACT Section:

36 on ACT English

36 on ACT Math

36 on ACT Reading

36 on ACT Science

Series: How to Get to 24 on Each ACT Section:

24 on ACT English

24 on ACT Math

24 on ACT Reading

24 on ACT Science

What ACT target score should you be aiming for?

ACT Vocabulary You Must Know

ACT Writing: 15 Tips to Raise Your Essay Score

How to Get Into Harvard and the Ivy League

How to Get a Perfect 4.0 GPA

How to Write an Amazing College Essay

What Exactly Are Colleges Looking For?

Is the ACT easier than the SAT? A Comprehensive Guide

Should you retake your SAT or ACT?

When should you take the SAT or ACT?

Stay Informed

Get the latest articles and test prep tips!

Looking for Graduate School Test Prep?

Check out our top-rated graduate blogs here:

GRE Online Prep Blog

GMAT Online Prep Blog

TOEFL Online Prep Blog

Holly R. "I am absolutely overjoyed and cannot thank you enough for helping me!”

•    Solve Trigonometry Functions Without a Calculator

Apply as a tutor to teach students online from anywhere in the world.

Solve trigonometry functions without a calculator.

• Chloe Daniel
• Published On: March 05 ,2024

Trigonometry is the branch of mathematics that deals with the study of angles and their numerical calculations. Calculators come in handy while solving trigonometric functions because of their in-built sin, cos, and tan functions. However, if you want to be a math wizard and exercise your brain, you can do this simple math without a calculator easily.

Before learning how to challenge yourself with interesting trigonometry exercises, let’s understand its basics.

Branches of Trigonometry

There are three sub-branches of trigonometry:

1. Plane Trigonometry

Plane Trigonometry deals with the two-dimensional plane of a triangle. It states that when enough sides and angles of triangles are known, the remaining can be calculated easily using trigonometric functions. 

The two important laws mathematicians use to find the unknown sides and angles of the triangle are the law of sines and the law of cosines. To maintain consistency, the angles of the triangles are named A, B, and C; whereas, the sides of the triangle are called a, b, and c.

2. Spherical Trigonometry

Spherical Trigonometry involves the study of spherical triangles, formed due to the intersection of three big circle arcs on the surface of the sphere. Spherical triangles are different from planar ones because the sum of their angles exceeds the sum of angles in a flat triangle. 

Functions of spherical triangles include the angles (A, B, and C) sides (a, b, and c), and the dihedral angles (α, β, and γ).

A list of common spherical trigonometry formulas is given below:

Basic Trigonometric Concepts

In a right-angled triangle, we have the following three sides:

Perpendicular — the vertical side beside the right angle i.e., a.

Hypotenuse — the longest side opposite to the right angle i.e., c.

Base — The adjacent side to the angle θ i.e., b.

Watch CBS News

Teens come up with trigonometry proof for Pythagorean Theorem, a problem that stumped math world for centuries

By Bill Whitaker

May 5, 2024 / 7:00 PM EDT / CBS News

As the school year ends, many students will be only too happy to see math classes in their rearview mirrors. It may seem to some of us non-mathematicians that geometry and trigonometry were created by the Greeks as a form of torture, so imagine our amazement when we heard two high school seniors had proved a mathematical puzzle that was thought to be impossible for 2,000 years. 

We met Calcea Johnson and Ne'Kiya Jackson at their all-girls Catholic high school in New Orleans. We expected to find two mathematical prodigies.

Instead, we found at St. Mary's Academy , all students are told their possibilities are boundless.

Come Mardi Gras season, New Orleans is alive with colorful parades, replete with floats, and beads, and high school marching bands.

In a city where uniqueness is celebrated, St. Mary's stands out – with young African American women playing trombones and tubas, twirling batons and dancing - doing it all, which defines St. Mary's, students told us.

Junior Christina Blazio says the school instills in them they have the ability to accomplish anything. 

Christina Blazio: That is kinda a standard here. So we aim very high - like, our aim is excellence for all students. 

The private Catholic elementary and high school sits behind the Sisters of the Holy Family Convent in New Orleans East. The academy was started by an African American nun for young Black women just after the Civil War. The church still supports the school with the help of alumni.

In December 2022, seniors Ne'Kiya Jackson and Calcea Johnson were working on a school-wide math contest that came with a cash prize.

Ne'Kiya Jackson: I was motivated because there was a monetary incentive.

Calcea Johnson: 'Cause I was like, "$500 is a lot of money. So I-- I would like to at least try."

Both were staring down the thorny bonus question.

Bill Whitaker: So tell me, what was this bonus question?

Calcea Johnson: It was to create a new proof of the Pythagorean Theorem. And it kind of gave you a few guidelines on how would you start a proof.

The seniors were familiar with the Pythagorean Theorem, a fundamental principle of geometry. You may remember it from high school: a² + b² = c². In plain English, when you know the length of two sides of a right triangle, you can figure out the length of the third.

Both had studied geometry and some trigonometry, and both told us math was not easy. What no one told  them  was there had been more than 300 documented proofs of the Pythagorean Theorem using algebra and geometry, but for 2,000 years a proof using trigonometry was thought to be impossible, … and that was the bonus question facing them.

Bill Whitaker: When you looked at the question did you think, "Boy, this is hard"?

Ne'Kiya Jackson: Yeah. 

Bill Whitaker: What motivated you to say, "Well, I'm going to try this"?

Calcea Johnson: I think I was like, "I started something. I need to finish it." 

Bill Whitaker: So you just kept on going.

Calcea Johnson: Yeah.

For two months that winter, they spent almost all their free time working on the proof.

CeCe Johnson: She was like, "Mom, this is a little bit too much."

CeCe and Cal Johnson are Calcea's parents.

CeCe Johnson:   So then I started looking at what she really was doing. And it was pages and pages and pages of, like, over 20 or 30 pages for this one problem.

Cal Johnson: Yeah, the garbage can was full of papers, which she would, you know, work out the problems and-- if that didn't work she would ball it up, throw it in the trash. 

Bill Whitaker: Did you look at the problem? 

Neliska Jackson is Ne'Kiya's mother.

Neliska Jackson: Personally I did not. 'Cause most of the time I don't understand what she's doing (laughter).

Michelle Blouin Williams: What if we did this, what if I write this? Does this help? ax² plus ….

Their math teacher, Michelle Blouin Williams, initiated the math contest.

Bill Whitaker: And did you think anyone would solve it?

Michelle Blouin Williams: Well, I wasn't necessarily looking for a solve. So, no, I didn't—

Bill Whitaker: What were you looking for?

Michelle Blouin Williams: I was just looking for some ingenuity, you know—

Calcea and Ne'Kiya delivered on that! They tried to explain their groundbreaking work to 60 Minutes. Calcea's proof is appropriately titled the Waffle Cone.

Calcea Johnson: So to start the proof, we start with just a regular right triangle where the angle in the corner is 90°. And the two angles are alpha and beta.

Bill Whitaker: Uh-huh

Calcea Johnson: So then what we do next is we draw a second congruent, which means they're equal in size. But then we start creating similar but smaller right triangles going in a pattern like this. And then it continues for infinity. And eventually it creates this larger waffle cone shape.

Calcea Johnson: Am I going a little too—

Bill Whitaker: You've been beyond me since the beginning. (laughter) 

Bill Whitaker: So how did you figure out the proof?

Ne'Kiya Jackson: Okay. So you have a right triangle, 90° angle, alpha and beta.

Bill Whitaker: Then what did you do?

Ne'Kiya Jackson: Okay, I have a right triangle inside of the circle. And I have a perpendicular bisector at OP to divide the triangle to make that small right triangle. And that's basically what I used for the proof. That's the proof.

Bill Whitaker: That's what I call amazing.

Ne'Kiya Jackson: Well, thank you.

There had been one other documented proof of the theorem using trigonometry by mathematician Jason Zimba in 2009 – one in 2,000 years. Now it seems Ne'Kiya and Calcea have joined perhaps the most exclusive club in mathematics. 

Bill Whitaker: So you both independently came up with proof that only used trigonometry.

Ne'Kiya Jackson: Yes.

Bill Whitaker: So are you math geniuses?

Calcea Johnson: I think that's a stretch. 

Bill Whitaker: If not genius, you're really smart at math.

Ne'Kiya Jackson: Not at all. (laugh) 

To document Calcea and Ne'Kiya's work, math teachers at St. Mary's submitted their proofs to an American Mathematical Society conference in Atlanta in March 2023.

Ne'Kiya Jackson: Well, our teacher approached us and was like, "Hey, you might be able to actually present this," I was like, "Are you joking?" But she wasn't. So we went. I got up there. We presented and it went well, and it blew up.

Bill Whitaker: It blew up.

Calcea Johnson: Yeah. 

Ne'Kiya Jackson: It blew up.

Bill Whitaker: Yeah. What was the blowup like?

Calcea Johnson: Insane, unexpected, crazy, honestly.

It took millenia to prove, but just a minute for word of their accomplishment to go around the world. They got a write-up in South Korea and a shout-out from former first lady Michelle Obama, a commendation from the governor and keys to the city of New Orleans. 

Bill Whitaker: Why do you think so many people found what you did to be so impressive?

Ne'Kiya Jackson: Probably because we're African American, one. And we're also women. So I think-- oh, and our age. Of course our ages probably played a big part.

Bill Whitaker: So you think people were surprised that young African American women, could do such a thing?

Calcea Johnson: Yeah, definitely.

Ne'Kiya Jackson: I'd like to actually be celebrated for what it is. Like, it's a great mathematical achievement.

Achievement, that's a word you hear often around St. Mary's academy. Calcea and Ne'Kiya follow a long line of barrier-breaking graduates. 

The late queen of Creole cooking, Leah Chase , was an alum. so was the first African-American female New Orleans police chief, Michelle Woodfork …

And judge for the Fifth Circuit Court of Appeals, Dana Douglas. Math teacher Michelle Blouin Williams told us Calcea and Ne'Kiya are typical St. Mary's students.  

Bill Whitaker: They're not unicorns.

Michelle Blouin Williams: Oh, no no. If they are unicorns, then every single lady that has matriculated through this school is a beautiful, Black unicorn.

Pamela Rogers: You're good?

Pamela Rogers, St. Mary's president and interim principal, told us the students hear that message from the moment they walk in the door.

Pamela Rogers: We believe all students can succeed, all students can learn. It does not matter the environment that you live in. 

Bill Whitaker: So when word went out that two of your students had solved this almost impossible math problem, were they universally applauded?

Pamela Rogers: In this community, they were greatly applauded. Across the country, there were many naysayers.

Bill Whitaker: What were they saying?

Pamela Rogers: They were saying, "Oh, they could not have done it. African Americans don't have the brains to do it." Of course, we sheltered our girls from that. But we absolutely did not expect it to come in the volume that it came.  

Bill Whitaker: And after such a wonderful achievement.

Pamela Rogers: People-- have a vision of who can be successful. And-- to some people, it is not always an African American female. And to us, it's always an African American female.

Gloria Ladson-Billings: What we know is when teachers lay out some expectations that say, "You can do this," kids will work as hard as they can to do it.

Gloria Ladson-Billings, professor emeritus at the University of Wisconsin, has studied how best to teach African American students. She told us an encouraging teacher can change a life.

Bill Whitaker: And what's the difference, say, between having a teacher like that and a whole school dedicated to the excellence of these students?

Gloria Ladson-Billings: So a whole school is almost like being in Heaven. 

Bill Whitaker: What do you mean by that?

Gloria Ladson-Billings: Many of our young people have their ceilings lowered, that somewhere around fourth or fifth grade, their thoughts are, "I'm not going to be anything special." What I think is probably happening at St. Mary's is young women come in as, perhaps, ninth graders and are told, "Here's what we expect to happen. And here's how we're going to help you get there."

At St. Mary's, half the students get scholarships, subsidized by fundraising to defray the $8,000 a year tuition. Here, there's no test to get in, but expectations are high and rules are strict: no cellphones, modest skirts, hair must be its natural color.

Students Rayah Siddiq, Summer Forde, Carissa Washington, Tatum Williams and Christina Blazio told us they appreciate the rules and rigor.

Rayah Siddiq: Especially the standards that they set for us. They're very high. And I don't think that's ever going to change.

Bill Whitaker: So is there a heart, a philosophy, an essence to St. Mary's?

Summer Forde: The sisterhood—

Carissa Washington: Sisterhood.

Tatum Williams: Sisterhood.

Bill Whitaker: The sisterhood?

Voices: Yes.

Bill Whitaker: And you don't mean the nuns. You mean-- (laughter)

Christina Blazio: I mean, yeah. The community—

Bill Whitaker: So when you're here, there's just no question that you're going to go on to college.

Rayah Siddiq: College is all they talk about. (laughter) 

Pamela Rogers: … and Arizona State University (Cheering)

Principal Rogers announces to her 615 students the colleges where every senior has been accepted.

Bill Whitaker: So for 17 years, you've had a 100% graduation rate—

Pamela Rogers: Yes.

Bill Whitaker: --and a 100% college acceptance rate?

Pamela Rogers: That's correct.

Last year when Ne'Kiya and Calcea graduated, all their classmates went to college and got scholarships. Ne'Kiya got a full ride to the pharmacy school at Xavier University in New Orleans. Calcea, the class valedictorian, is studying environmental engineering at Louisiana State University.

Bill Whitaker: So wait a minute. Neither one of you is going to pursue a career in math?

Both: No. (laugh)

Calcea Johnson: I may take up a minor in math. But I don't want that to be my job job.

Ne'Kiya Jackson: Yeah. People might expect too much out of me if (laugh) I become a mathematician. (laugh)

But math is not completely in their rear-view mirrors. This spring they submitted their high school proofs for final peer review and publication … and are still working on further proofs of the Pythagorean Theorem. Since their first two …

Calcea Johnson: We found five. And then we found a general format that could potentially produce at least five additional proofs.

Bill Whitaker: And you're not math geniuses?

Bill Whitaker: I'm not buying it. (laughs)

Produced by Sara Kuzmarov. Associate producer, Mariah B. Campbell. Edited by Daniel J. Glucksman.

Bill Whitaker is an award-winning journalist and 60 Minutes correspondent who has covered major news stories, domestically and across the globe, for more than four decades with CBS News.

More from CBS News

Cuban spies behind sale of American secrets around the world

Pope Francis says "the globalization of indifference is a very ugly disease"

How a spy for Cuba got away with sharing America's secrets for 17 years

Nazi's photo album shows life of a top Auschwitz officer

ChatGPT’s Next Magic Trick Is Singing and Solving Math Problems With Your Phone Camera

GPT-4o responds as fast as humans.

ChatGPT 4 may still be relatively new, but OpenAI is already iterating with an upgrade that can respond as quickly as humans do in normal conversation. The company showed off GPT-4o in a live demo , showing off its ability to use your phone’s camera to solve math equations and deliver a much more conversational voice assistant experience.

While we only have the event demo to go off of, GPT-4o looks impressive. It doesn’t even have to wait for you to finish your request and can roll with interruptions mid-prompt, bringing one step closer to living out Her in real life.

Even Faster Response Times

According to OpenAI, the GPT-4o model can respond as fast as 232 milliseconds to audio inputs. More realistically, it averages around 320 milliseconds to respond, which OpenAI said is similar to how fast humans respond in conversation.

On top of the speed, GPT-4o can handle interruptions and any adjustment requests. As seen in the bedtime story demo, GPT-4o immediately stopped talking when interrupted and quickly handled requests like adding more dramatic inflections, narrating in a robot voice, and even singing the entire prompt out loud. If that demo doesn’t convince you, two GPT-4o models improvising a song together should.

GPT-4o isn’t just more responsive to voice, it can also see better. The new vision features allow it to see through your device’s camera and understand things like handwritten math equations or messages . It’s eerie how genuinely touched GPT-4o sounds when it sees and understands a message that says “I Heart ChatGPT.” Even more impressive, GPT-4o can handle coding tasks and live translations between two people. This should feel way more natural than Google Translate when you’re trying to have a conversation in a foreign country.

Available for Free

OpenAI said the text and image capabilities for GPT-4o roll out today, but the voice feature will be coming to alpha within ChatGPT Plus in the coming weeks. Once it’s fully ready, the upgraded ChatGPT model will be available to all users, subscribers or otherwise. However, if you pay $20 per month for ChatGPT Plus , you’ll get five times the message limits of GPT-4o compared to the free version.

Anytime a large language model gets such an impressive update, we have to consider the potential for misuse . Considering how smoothly the live demo for solving the equation went, it looks like an even better way to help students get out of their math homework. However, OpenAI said that GPT-4o was built with new safety systems to offer guardrails on voice outputs. We’ll have to wait and see if these guardrails are enough.

• Sustainability
• Small Business
• Kickstarting the next generation of blockchain payments

Five startups will join Mastercard’s Start Path Blockchain and Digital Assets program to explore how people and businesses use money to move value and solve real-world problems

Today, Mastercard is introducing five startups from around the world to its Start Path Blockchain and Digital Assets program to drive best-in-class user experiences and expand use cases that demonstrate the power of blockchain technology.

Blockchain and digital assets are already transforming financial services, expanding how people and businesses can use their money to move value. Digital assets are becoming increasingly mainstream, speeding up commerce with trust and transparency.

Each currency format – from regulated money to bank deposits, to stablecoins and CBDCs – serves a specific purpose, and Mastercard is connecting with industry experts and fintechs to explore differentiated use cases that can help to solve real-world problems. Mastercard’s experience in payments innovation and building a global, card-based payments network uniquely positions the company to bridge these ecosystems with startups, power new solutions and create efficiencies in digital commerce experiences.

As part of its collaborative approach to innovation, Mastercard is exploring future use cases to scale new solutions with startups around the world. High-potential blockchain, digital assets and Web3 startups receive the opportunity for collaboration, bespoke training and access to Mastercard’s customers and channels through the virtual four-month program. Since the program was founded in 2014, Mastercard has supported more than 400 startups from 54 countries.

The following startups are joining Start Path to expand into new markets and scale blockchain innovation:

Kulipa (France): Enables next-gen crypto payment card issuing for digital wallets 

Parfin (U.K.): Builds enterprise-grade software products to allow financial institutions to adopt blockchain rails 

peaq (Singapore): Provides permissionless, borderless digital infrastructure for real-world apps (DePIN), leveraging vehicles, machines, robots and devices

Triangle (USA): Prioritizes sustainability through a data platform that triangulates climate data with finance 

Venly (Belgium): Makes blockchain integration straightforward for developers and businesses to support industry growth and digital transformation  

Media contact: Jen Langione, Mastercard Global Communications, (917) 408-2941, [email protected]

• Perspectives
• Investor Relations

Mastercard Sites

• Mastercard.com
• Mastercard Brand Center
• Mastercard Data & Services
• Priceless.com