regression analysis in marketing research

• Media Center
• E-Books & White Papers
• Knowledge Center

The Strategic Value of Regression Analysis in Marketing Research

by Michael Lieberman , on December 14, 2023

Regression analysis offers significant value in modern business and research contexts. This article explores the strategic importance of regression analysis to shed light on its diverse applications and benefits. Included are several different case studies to help bring the concept to life.

Understanding Regression Analysis in Marketing

Regression analysis in marketing is used to examine how independent variables—such as advertising spend, demographics, pricing, and product features—influence a dependent variable, typically a measure of consumer behavior or business performance. The goal is to create models that capture these relationships accurately, allowing marketers to make informed decisions.

Benefits of Regression Analysis in Marketing

• Data-driven decisions : Regression analysis empowers marketers to make data-driven decisions, reducing reliance on intuition and guesswork. This approach leads to more accurate and strategic marketing efforts.
• Efficiency and cost savings : By optimizing marketing campaigns and resource allocation, regression analysis can significantly improve efficiency and cost-effectiveness. Companies can achieve better results with the same or fewer resources.
• Personalization : Understanding consumer behavior through regression analysis allows for personalized marketing efforts. Tailored messages and offers can lead to higher engagement and conversion rates.
• Competitive advantage : Marketers who employ regression analysis are better equipped to adapt to changing market conditions, outperform competitors, and stay ahead of industry trends.
• Continuous improvement : Regression analysis is an iterative process. As new data becomes available, models can be updated and refined, ensuring that marketing strategies remain effective over time.

Strategic Applications

• Consumer behavior prediction : Regression analysis helps marketers predict consumer behavior. By analyzing historical data and considering various factors, such as past purchases, online behavior, and demographic information, companies can build models to anticipate customer preferences, buying patterns, and churn rates.
• Marketing campaign optimization : Businesses invest heavily in marketing campaigns. Regression analysis aids in optimizing these efforts by identifying which marketing channels, messages, or strategies have the greatest impact on key performance indicators (KPIs) like sales, click-through rates, or conversion rates.
• Pricing strategy : Pricing is a critical aspect of marketing. Regression analysis can reveal the relationship between pricing strategies and sales volume, helping companies determine the optimal price points for their products or services.
• Product Development : In product development, regression analysis can be used to understand the relationship between product features and consumer satisfaction. Companies can then prioritize product enhancements based on customer preferences.

Case Study – Regression Analysis for Ranking Key Attributes

Let’s explore a specific example in a category known as Casual Dining Restaurants (CDR). In a survey, respondents are asked to rate several casual dining restaurants on a variety of attributes. For the purposes of this article, we will keep the number of demonstrated attributes to the top eight. The data for each restaurant is stacked into one regression. We are seeking to rank the attributes based on a regression analysis against an industry standard overall measurement: Net Promoter Score.

Table 1 shows the leading Casual Dining Restaurant chains in the United States to be used to ‘rank’ the key reasons that patrons visit this restaurant category, not specific to one restaurant band.

Table 1 - List of Leading Casual Dining Restaurant Chains in the United States

In Figure 1 we see a graphic example of key drivers across the CDR category.

The category-wide drivers of CDR visits are not particularly surprising. Good food. Good value. Cleanliness. Staff energy. There is one attribute, however, that may not seem intuitively as important as restaurant executives might think. Make sure your servers thank departing customers . Diners seek not just delicious cuisine at a reasonable price, but they also desire a sense of appreciation.

Case Study – Regression and Brand Response to Crisis

A major automobile company has a public relations disaster. In order to regain trust in their brand equity, the company commissions a series of regression analyses to gauge how buyers are viewing their brand image. However, what they really want to know is how American auto buyers view trust—the most valuable brand perception of this company’s automotive product.

The disaster is fresh—a nation-wide recall of thousands of cars over safety issues regarding airbags—so our company would like a composite of which values go into “Is this a Company I Trust.” Thus, it surveyed decision makers, stake holders, owners, and prospects. We then stack the data into one dataset and run a strategic regression. Once performed, the regression beta values are summed and then reported as percentages of influence on the dependent variable. What we see are the major components of “Trust.”

Figure 2 - Percentage Influence of "A Company I Trust"

Not surprisingly, family safety is the leading driver of Trust. However, we now have Shapley Values of the major components. These findings would normally be handed over to the public relations team to begin damage control. Within days the company began to run advertisements in major markets to reverse the negative narrative of the recall.

Case Study - Regression Analysis/Maximizing Product Lines

SparkleSquad Studios is a fictional startup hoping to find a niche among tween and teen girls to help reverse the tide of social media addiction. Though funded through venture capital investment, they found that all their 40 potential product areas, they only have capacity to produce eight. In order to determine the top 8 hobby products in demand, they fielded a study.

Table 2 - List of Potential Product Area Development

SparkleSquad Studios then conducted a large study gathering data from thousands of web-based surveys conducted among girls aged 10 to 16 across the United States. The key construct of the study is simple—not more than 5 minutes—and concise to cater to respondents' shorter attention spans. Below are the key questions.

• How much money do you typically allocate to hobbies unrelated to social media in a given month?
• Please check-off the hobbies that interest you from the list of 40 potential options below.

Question 1 serves as the dependent variable in the regression. Question 2 responses are coded into categorical variables, 1=Checked, 0=Not Checked . These are the independent variables.

Results are shown below in Table 3.

Table 3 - Top 10 Hobby Products for Production Determined Through Regression Analysis

Based on the resulting regression analysis, SparkleSquad will commence production of ten statistically significant products. The data-driven approach ensures these offerings meet the maximized determined market demand.

Regression analysis gives businesses the ability to predict consumer behavior, optimize marketing efforts, and drive results through data-driven decision-making. By leveraging regression analysis, businesses can gain a competitive advantage and increase their efficiency, and effectiveness. In an era where consumer preferences and market conditions are in constant flux, regression analysis remains an essential tool for marketers looking to stay ahead of the curve.

Michael Lieberman is the Founder and President of Multivariate Solutions , a statistical and market research consulting firm that works with major advertising, public relations, and political strategy firms. He can be reached at +1 646 257 3794, or [email protected] .

About This Blog

Our goal is to help you better understand your customer, market, and competition in order to help drive your business growth.

Popular Posts

• A CEO’s Perspective on Harnessing AI for Market Research Excellence
• 7 Key Advantages of Outsourcing Market Research Services
• How to Use Market Research for Onboarding and Training Employees
• 10 Global Industries That Will Boom in the Next 5 Years
• Primary Data vs. Secondary Data: Market Research Methods

Recent Posts

Posts by topic.

• Industry Insights (828)
• Market Research Strategy (273)
• Food & Beverage (134)
• Healthcare (125)
• The Freedonia Group (121)
• How To's (109)
• Market Research Provider (93)
• Manufacturing & Construction (81)
• Pharmaceuticals (80)
• Packaged Facts (78)
• Telecommunications & Wireless (70)
• Heavy Industry (69)
• Marketing (58)
• Profound (57)
• Retail (56)
• Software & Enterprise Computing (55)
• Transportation & Shipping (54)
• House & Home (50)
• Materials & Chemicals (47)
• Medical Devices (46)
• Consumer Electronics (45)
• Energy & Resources (42)
• Public Sector (40)
• Biotechnology (37)
• Demographics (37)
• Business Services & Administration (36)
• Education (36)
• Custom Market Research (35)
• Diagnostics (34)
• Academic (33)
• Travel & Leisure (33)
• E-commerce & IT Outsourcing (32)
• Financial Services (29)
• Computer Hardware & Networking (26)
• Simba Information (24)
• Kalorama Information (21)
• Knowledge Centers (19)
• Apparel (18)
• Cosmetics & Personal Care (17)
• Social Media (16)
• Market Research Subscription (15)
• Advertising (14)
• Big Data (14)
• Holiday (11)
• Emerging Markets (8)
• Associations (1)
• Religion (1)

MarketResearch.com 6116 Executive Blvd Suite 550 Rockville, MD 20852 800.298.5699 (U.S.) +1.240.747.3093 (International) [email protected]

From Our Blog

Subscribe to blog, connect with us.

• Business Essentials
• Leadership & Management
• Credential of Leadership, Impact, and Management in Business (CLIMB)
• Entrepreneurship & Innovation
• Digital Transformation
• Finance & Accounting
• Business in Society
• For Organizations
• Support Portal
• Media Coverage
• Founding Donors
• Leadership Team

• Harvard Business School →
• HBS Online →
• Business Insights →

Business Insights

Harvard Business School Online's Business Insights Blog provides the career insights you need to achieve your goals and gain confidence in your business skills.

• Career Development
• Communication
• Decision-Making
• Earning Your MBA
• Negotiation
• News & Events
• Productivity
• Staff Spotlight
• Student Profiles
• Work-Life Balance
• AI Essentials for Business
• Alternative Investments
• Business Analytics
• Business Strategy
• Business and Climate Change
• Design Thinking and Innovation
• Digital Marketing Strategy
• Disruptive Strategy
• Economics for Managers
• Entrepreneurship Essentials
• Financial Accounting
• Global Business
• Launching Tech Ventures
• Leadership Principles
• Leadership, Ethics, and Corporate Accountability
• Leading Change and Organizational Renewal
• Leading with Finance
• Management Essentials
• Negotiation Mastery
• Organizational Leadership
• Power and Influence for Positive Impact
• Strategy Execution
• Sustainable Business Strategy
• Sustainable Investing
• Winning with Digital Platforms

What Is Regression Analysis in Business Analytics?

• 14 Dec 2021

Countless factors impact every facet of business. How can you consider those factors and know their true impact?

Imagine you seek to understand the factors that influence people’s decision to buy your company’s product. They range from customers’ physical locations to satisfaction levels among sales representatives to your competitors' Black Friday sales.

Understanding the relationships between each factor and product sales can enable you to pinpoint areas for improvement, helping you drive more sales.

To learn how each factor influences sales, you need to use a statistical analysis method called regression analysis .

If you aren’t a business or data analyst, you may not run regressions yourself, but knowing how analysis works can provide important insight into which factors impact product sales and, thus, which are worth improving.

Access your free e-book today.

Foundational Concepts for Regression Analysis

Before diving into regression analysis, you need to build foundational knowledge of statistical concepts and relationships.

Independent and Dependent Variables

Start with the basics. What relationship are you aiming to explore? Try formatting your answer like this: “I want to understand the impact of [the independent variable] on [the dependent variable].”

The independent variable is the factor that could impact the dependent variable . For example, “I want to understand the impact of employee satisfaction on product sales.”

In this case, employee satisfaction is the independent variable, and product sales is the dependent variable. Identifying the dependent and independent variables is the first step toward regression analysis.

Correlation vs. Causation

One of the cardinal rules of statistically exploring relationships is to never assume correlation implies causation. In other words, just because two variables move in the same direction doesn’t mean one caused the other to occur.

If two or more variables are correlated , their directional movements are related. If two variables are positively correlated , it means that as one goes up or down, so does the other. Alternatively, if two variables are negatively correlated , one goes up while the other goes down.

A correlation’s strength can be quantified by calculating the correlation coefficient , sometimes represented by r . The correlation coefficient falls between negative one and positive one.

r = -1 indicates a perfect negative correlation.

r = 1 indicates a perfect positive correlation.

r = 0 indicates no correlation.

Causation means that one variable caused the other to occur. Proving a causal relationship between variables requires a true experiment with a control group (which doesn’t receive the independent variable) and an experimental group (which receives the independent variable).

While regression analysis provides insights into relationships between variables, it doesn’t prove causation. It can be tempting to assume that one variable caused the other—especially if you want it to be true—which is why you need to keep this in mind any time you run regressions or analyze relationships between variables.

With the basics under your belt, here’s a deeper explanation of regression analysis so you can leverage it to drive strategic planning and decision-making.

Related: How to Learn Business Analytics without a Business Background

What Is Regression Analysis?

Regression analysis is the statistical method used to determine the structure of a relationship between two variables (single linear regression) or three or more variables (multiple regression).

According to the Harvard Business School Online course Business Analytics , regression is used for two primary purposes:

• To study the magnitude and structure of the relationship between variables
• To forecast a variable based on its relationship with another variable

Both of these insights can inform strategic business decisions.

“Regression allows us to gain insights into the structure of that relationship and provides measures of how well the data fit that relationship,” says HBS Professor Jan Hammond, who teaches Business Analytics, one of three courses that comprise the Credential of Readiness (CORe) program . “Such insights can prove extremely valuable for analyzing historical trends and developing forecasts.”

One way to think of regression is by visualizing a scatter plot of your data with the independent variable on the X-axis and the dependent variable on the Y-axis. The regression line is the line that best fits the scatter plot data. The regression equation represents the line’s slope and the relationship between the two variables, along with an estimation of error.

Physically creating this scatter plot can be a natural starting point for parsing out the relationships between variables.

Types of Regression Analysis

There are two types of regression analysis: single variable linear regression and multiple regression.

Single variable linear regression is used to determine the relationship between two variables: the independent and dependent. The equation for a single variable linear regression looks like this:

In the equation:

• ŷ is the expected value of Y (the dependent variable) for a given value of X (the independent variable).
• x is the independent variable.
• α is the Y-intercept, the point at which the regression line intersects with the vertical axis.
• β is the slope of the regression line, or the average change in the dependent variable as the independent variable increases by one.
• ε is the error term, equal to Y – ŷ, or the difference between the actual value of the dependent variable and its expected value.

Multiple regression , on the other hand, is used to determine the relationship between three or more variables: the dependent variable and at least two independent variables. The multiple regression equation looks complex but is similar to the single variable linear regression equation:

Each component of this equation represents the same thing as in the previous equation, with the addition of the subscript k, which is the total number of independent variables being examined. For each independent variable you include in the regression, multiply the slope of the regression line by the value of the independent variable, and add it to the rest of the equation.

How to Run Regressions

You can use a host of statistical programs—such as Microsoft Excel, SPSS, and STATA—to run both single variable linear and multiple regressions. If you’re interested in hands-on practice with this skill, Business Analytics teaches learners how to create scatter plots and run regressions in Microsoft Excel, as well as make sense of the output and use it to drive business decisions.

Calculating Confidence and Accounting for Error

It’s important to note: This overview of regression analysis is introductory and doesn’t delve into calculations of confidence level, significance, variance, and error. When working in a statistical program, these calculations may be provided or require that you implement a function. When conducting regression analysis, these metrics are important for gauging how significant your results are and how much importance to place on them.

Why Use Regression Analysis?

Once you’ve generated a regression equation for a set of variables, you effectively have a roadmap for the relationship between your independent and dependent variables. If you input a specific X value into the equation, you can see the expected Y value.

This can be critical for predicting the outcome of potential changes, allowing you to ask, “What would happen if this factor changed by a specific amount?”

Returning to the earlier example, running a regression analysis could allow you to find the equation representing the relationship between employee satisfaction and product sales. You could input a higher level of employee satisfaction and see how sales might change accordingly. This information could lead to improved working conditions for employees, backed by data that shows the tie between high employee satisfaction and sales.

Whether predicting future outcomes, determining areas for improvement, or identifying relationships between seemingly unconnected variables, understanding regression analysis can enable you to craft data-driven strategies and determine the best course of action with all factors in mind.

Do you want to become a data-driven professional? Explore our eight-week Business Analytics course and our three-course Credential of Readiness (CORe) program to deepen your analytical skills and apply them to real-world business problems.

About the Author

Root out friction in every digital experience, super-charge conversion rates, and optimize digital self-service

Uncover insights from any interaction, deliver AI-powered agent coaching, and reduce cost to serve

Increase revenue and loyalty with real-time insights and recommendations delivered to teams on the ground

Know how your people feel and empower managers to improve employee engagement, productivity, and retention

Take action in the moments that matter most along the employee journey and drive bottom line growth

Whatever they’re are saying, wherever they’re saying it, know exactly what’s going on with your people

Get faster, richer insights with qual and quant tools that make powerful market research available to everyone

Run concept tests, pricing studies, prototyping + more with fast, powerful studies designed by UX research experts

Track your brand performance 24/7 and act quickly to respond to opportunities and challenges in your market

Explore the platform powering Experience Management

• Free Account
• For Digital
• For Customer Care
• For Human Resources
• For Researchers
• Financial Services
• All Industries

Popular Use Cases

• Customer Experience
• Employee Experience
• Net Promoter Score
• Voice of Customer
• Customer Success Hub
• Product Documentation
• Training & Certification
• XM Institute
• Popular Resources
• Customer Stories
• Artificial Intelligence
• Market Research
• Partnerships
• Marketplace

The annual gathering of the experience leaders at the world’s iconic brands building breakthrough business results, live in Salt Lake City.

• English/AU & NZ
• Español/Europa
• Español/América Latina
• Português Brasileiro
• REQUEST DEMO
• Experience Management
• Survey Data Analysis & Reporting
• Regression Analysis

Try Qualtrics for free

The complete guide to regression analysis.

19 min read What is regression analysis and why is it useful? While most of us have heard the term, understanding regression analysis in detail may be something you need to brush up on. Here’s what you need to know about this popular method of analysis.

When you rely on data to drive and guide business decisions, as well as predict market trends, just gathering and analyzing what you find isn’t enough — you need to ensure it’s relevant and valuable.

The challenge, however, is that so many variables can influence business data: market conditions, economic disruption, even the weather! As such, it’s essential you know which variables are affecting your data and forecasts, and what data you can discard.

And one of the most effective ways to determine data value and monitor trends (and the relationships between them) is to use regression analysis, a set of statistical methods used for the estimation of relationships between independent and dependent variables.

In this guide, we’ll cover the fundamentals of regression analysis, from what it is and how it works to its benefits and practical applications.

Free eBook: 2024 global market research trends report

What is regression analysis?

Regression analysis is a statistical method. It’s used for analyzing different factors that might influence an objective – such as the success of a product launch, business growth, a new marketing campaign – and determining which factors are important and which ones can be ignored.

Regression analysis can also help leaders understand how different variables impact each other and what the outcomes are. For example, when forecasting financial performance, regression analysis can help leaders determine how changes in the business can influence revenue or expenses in the future.

Running an analysis of this kind, you might find that there’s a high correlation between the number of marketers employed by the company, the leads generated, and the opportunities closed.

This seems to suggest that a high number of marketers and a high number of leads generated influences sales success. But do you need both factors to close those sales? By analyzing the effects of these variables on your outcome,  you might learn that when leads increase but the number of marketers employed stays constant, there is no impact on the number of opportunities closed, but if the number of marketers increases, leads and closed opportunities both rise.

Regression analysis can help you tease out these complex relationships so you can determine which areas you need to focus on in order to get your desired results, and avoid wasting time with those that have little or no impact. In this example, that might mean hiring more marketers rather than trying to increase leads generated.

How does regression analysis work?

Regression analysis starts with variables that are categorized into two types: dependent and independent variables. The variables you select depend on the outcomes you’re analyzing.

Understanding variables:

1. dependent variable.

This is the main variable that you want to analyze and predict. For example, operational (O) data such as your quarterly or annual sales, or experience (X) data such as your net promoter score (NPS) or customer satisfaction score (CSAT) .

These variables are also called response variables, outcome variables, or left-hand-side variables (because they appear on the left-hand side of a regression equation).

There are three easy ways to identify them:

• Is the variable measured as an outcome of the study?
• Does the variable depend on another in the study?
• Do you measure the variable only after other variables are altered?

2. Independent variable

Independent variables are the factors that could affect your dependent variables. For example, a price rise in the second quarter could make an impact on your sales figures.

You can identify independent variables with the following list of questions:

• Is the variable manipulated, controlled, or used as a subject grouping method by the researcher?
• Does this variable come before the other variable in time?
• Are you trying to understand whether or how this variable affects another?

Independent variables are often referred to differently in regression depending on the purpose of the analysis. You might hear them called:

Explanatory variables

Explanatory variables are those which explain an event or an outcome in your study. For example, explaining why your sales dropped or increased.

Predictor variables

Predictor variables are used to predict the value of the dependent variable. For example, predicting how much sales will increase when new product features are rolled out .

Experimental variables

These are variables that can be manipulated or changed directly by researchers to assess the impact. For example, assessing how different product pricing ($10 vs $15 vs $20) will impact the likelihood to purchase.

Subject variables (also called fixed effects)

Subject variables can’t be changed directly, but vary across the sample. For example, age, gender, or income of consumers.

Unlike experimental variables, you can’t randomly assign or change subject variables, but you can design your regression analysis to determine the different outcomes of groups of participants with the same characteristics. For example, ‘how do price rises impact sales based on income?’

Carrying out regression analysis

So regression is about the relationships between dependent and independent variables. But how exactly do you do it?

Assuming you have your data collection done already, the first and foremost thing you need to do is plot your results on a graph. Doing this makes interpreting regression analysis results much easier as you can clearly see the correlations between dependent and independent variables.

Let’s say you want to carry out a regression analysis to understand the relationship between the number of ads placed and revenue generated.

On the Y-axis, you place the revenue generated. On the X-axis, the number of digital ads. By plotting the information on the graph, and drawing a line (called the regression line) through the middle of the data, you can see the relationship between the number of digital ads placed and revenue generated.

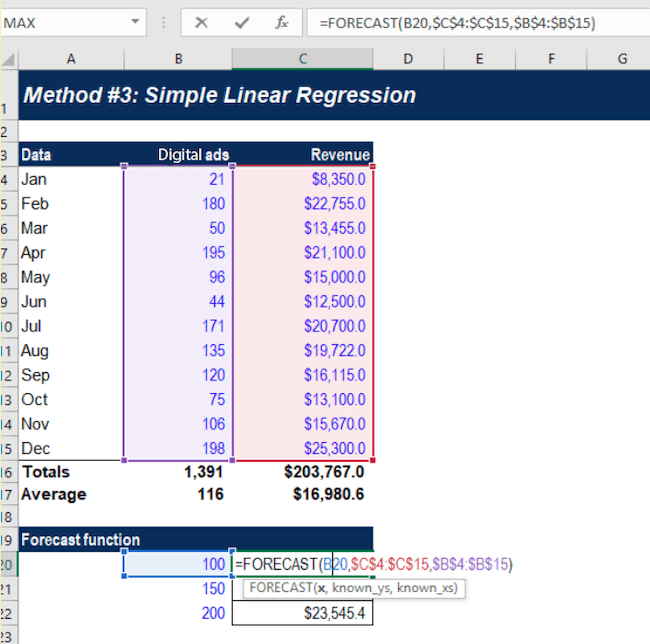
This regression line is the line that provides the best description of the relationship between your independent variables and your dependent variable. In this example, we’ve used a simple linear regression model.

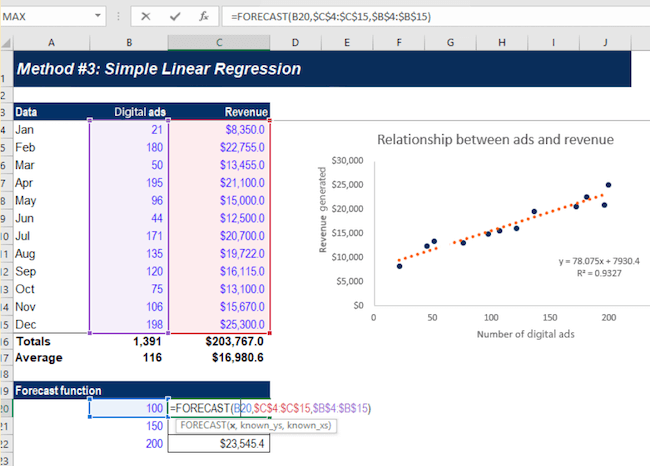
Statistical analysis software can draw this line for you and precisely calculate the regression line. The software then provides a formula for the slope of the line, adding further context to the relationship between your dependent and independent variables.

Simple linear regression analysis

A simple linear model uses a single straight line to determine the relationship between a single independent variable and a dependent variable.

This regression model is mostly used when you want to determine the relationship between two variables (like price increases and sales) or the value of the dependent variable at certain points of the independent variable (for example the sales levels at a certain price rise).

While linear regression is useful, it does require you to make some assumptions.

For example, it requires you to assume that:

• the data was collected using a statistically valid sample collection method that is representative of the target population
• The observed relationship between the variables can’t be explained by a ‘hidden’ third variable – in other words, there are no spurious correlations.
• the relationship between the independent variable and dependent variable is linear – meaning that the best fit along the data points is a straight line and not a curved one

Multiple regression analysis

As the name suggests, multiple regression analysis is a type of regression that uses multiple variables. It uses multiple independent variables to predict the outcome of a single dependent variable. Of the various kinds of multiple regression, multiple linear regression is one of the best-known.

Multiple linear regression is a close relative of the simple linear regression model in that it looks at the impact of several independent variables on one dependent variable. However, like simple linear regression, multiple regression analysis also requires you to make some basic assumptions.

For example, you will be assuming that:

• there is a linear relationship between the dependent and independent variables (it creates a straight line and not a curve through the data points)
• the independent variables aren’t highly correlated in their own right

An example of multiple linear regression would be an analysis of how marketing spend, revenue growth, and general market sentiment affect the share price of a company.

With multiple linear regression models you can estimate how these variables will influence the share price, and to what extent.

Multivariate linear regression

Multivariate linear regression involves more than one dependent variable as well as multiple independent variables, making it more complicated than linear or multiple linear regressions. However, this also makes it much more powerful and capable of making predictions about complex real-world situations.

For example, if an organization wants to establish or estimate how the COVID-19 pandemic has affected employees in its different markets, it can use multivariate linear regression, with the different geographical regions as dependent variables and the different facets of the pandemic as independent variables (such as mental health self-rating scores, proportion of employees working at home, lockdown durations and employee sick days).

Through multivariate linear regression, you can look at relationships between variables in a holistic way and quantify the relationships between them. As you can clearly visualize those relationships, you can make adjustments to dependent and independent variables to see which conditions influence them. Overall, multivariate linear regression provides a more realistic picture than looking at a single variable.

However, because multivariate techniques are complex, they involve high-level mathematics that require a statistical program to analyze the data.

Logistic regression

Logistic regression models the probability of a binary outcome based on independent variables.

So, what is a binary outcome? It’s when there are only two possible scenarios, either the event happens (1) or it doesn’t (0). e.g. yes/no outcomes, pass/fail outcomes, and so on. In other words, if the outcome can be described as being in either one of two categories.

Logistic regression makes predictions based on independent variables that are assumed or known to have an influence on the outcome. For example, the probability of a sports team winning their game might be affected by independent variables like weather, day of the week, whether they are playing at home or away and how they fared in previous matches.

What are some common mistakes with regression analysis?

Across the globe, businesses are increasingly relying on quality data and insights to drive decision-making — but to make accurate decisions, it’s important that the data collected and statistical methods used to analyze it are reliable and accurate.

Using the wrong data or the wrong assumptions can result in poor decision-making, lead to missed opportunities to improve efficiency and savings, and — ultimately — damage your business long term.

• Assumptions

When running regression analysis, be it a simple linear or multiple regression, it’s really important to check that the assumptions your chosen method requires have been met. If your data points don’t conform to a straight line of best fit, for example, you need to apply additional statistical modifications to accommodate the non-linear data. For example, if you are looking at income data, which scales on a logarithmic distribution, you should take the Natural Log of Income as your variable then adjust the outcome after the model is created.

• Correlation vs. causation

It’s a well-worn phrase that bears repeating – correlation does not equal causation. While variables that are linked by causality will always show correlation, the reverse is not always true. Moreover, there is no statistic that can determine causality (although the design of your study overall can).

If you observe a correlation in your results, such as in the first example we gave in this article where there was a correlation between leads and sales, you can’t assume that one thing has influenced the other. Instead, you should use it as a starting point for investigating the relationship between the variables in more depth.

• Choosing the wrong variables to analyze

Before you use any kind of statistical method, it’s important to understand the subject you’re researching in detail. Doing so means you’re making informed choices of variables and you’re not overlooking something important that might have a significant bearing on your dependent variable.

• Model building The variables you include in your analysis are just as important as the variables you choose to exclude. That’s because the strength of each independent variable is influenced by the other variables in the model. Other techniques, such as Key Drivers Analysis, are able to account for these variable interdependencies.

Benefits of using regression analysis

There are several benefits to using regression analysis to judge how changing variables will affect your business and to ensure you focus on the right things when forecasting.

Here are just a few of those benefits:

Make accurate predictions

Regression analysis is commonly used when forecasting and forward planning for a business. For example, when predicting sales for the year ahead, a number of different variables will come into play to determine the eventual result.

Regression analysis can help you determine which of these variables are likely to have the biggest impact based on previous events and help you make more accurate forecasts and predictions.

Identify inefficiencies

Using a regression equation a business can identify areas for improvement when it comes to efficiency, either in terms of people, processes, or equipment.

For example, regression analysis can help a car manufacturer determine order numbers based on external factors like the economy or environment.

Using the initial regression equation, they can use it to determine how many members of staff and how much equipment they need to meet orders.

Drive better decisions

Improving processes or business outcomes is always on the minds of owners and business leaders, but without actionable data, they’re simply relying on instinct, and this doesn’t always work out.

This is particularly true when it comes to issues of price. For example, to what extent will raising the price (and to what level) affect next quarter’s sales?

There’s no way to know this without data analysis. Regression analysis can help provide insights into the correlation between price rises and sales based on historical data.

How do businesses use regression? A real-life example

Marketing and advertising spending are common topics for regression analysis. Companies use regression when trying to assess the value of ad spend and marketing spend on revenue.

A typical example is using a regression equation to assess the correlation between ad costs and conversions of new customers. In this instance,

• our dependent variable (the factor we’re trying to assess the outcomes of) will be our conversions
• the independent variable (the factor we’ll change to assess how it changes the outcome) will be the daily ad spend
• the regression equation will try to determine whether an increase in ad spend has a direct correlation with the number of conversions we have

The analysis is relatively straightforward — using historical data from an ad account, we can use daily data to judge ad spend vs conversions and how changes to the spend alter the conversions.

By assessing this data over time, we can make predictions not only on whether increasing ad spend will lead to increased conversions but also what level of spending will lead to what increase in conversions. This can help to optimize campaign spend and ensure marketing delivers good ROI.

This is an example of a simple linear model. If you wanted to carry out a more complex regression equation, we could also factor in other independent variables such as seasonality, GDP, and the current reach of our chosen advertising networks.

By increasing the number of independent variables, we can get a better understanding of whether ad spend is resulting in an increase in conversions, whether it’s exerting an influence in combination with another set of variables, or if we’re dealing with a correlation with no causal impact – which might be useful for predictions anyway, but isn’t a lever we can use to increase sales.

Using this predicted value of each independent variable, we can more accurately predict how spend will change the conversion rate of advertising.

Regression analysis tools

Regression analysis is an important tool when it comes to better decision-making and improved business outcomes. To get the best out of it, you need to invest in the right kind of statistical analysis software.

The best option is likely to be one that sits at the intersection of powerful statistical analysis and intuitive ease of use, as this will empower everyone from beginners to expert analysts to uncover meaning from data, identify hidden trends and produce predictive models without statistical training being required.

To help prevent costly errors, choose a tool that automatically runs the right statistical tests and visualizations and then translates the results into simple language that anyone can put into action.

With software that’s both powerful and user-friendly, you can isolate key experience drivers, understand what influences the business, apply the most appropriate regression methods, identify data issues, and much more.

With Qualtrics’ Stats iQ™, you don’t have to worry about the regression equation because our statistical software will run the appropriate equation for you automatically based on the variable type you want to monitor. You can also use several equations, including linear regression and logistic regression, to gain deeper insights into business outcomes and make more accurate, data-driven decisions.

Related resources

Analysis & Reporting

Data Analysis 31 min read

Social media analytics 13 min read, kano analysis 21 min read, margin of error 11 min read, data saturation in qualitative research 8 min read, thematic analysis 11 min read, behavioral analytics 12 min read, request demo.

Ready to learn more about Qualtrics?

• SUGGESTED TOPICS
• The Magazine
• Newsletters
• Managing Yourself
• Managing Teams
• Work-life Balance
• The Big Idea
• Data & Visuals
• Reading Lists
• Case Selections
• HBR Learning
• Topic Feeds
• Account Settings
• Email Preferences

A Refresher on Regression Analysis

Understanding one of the most important types of data analysis.

You probably know by now that whenever possible you should be making data-driven decisions at work . But do you know how to parse through all the data available to you? The good news is that you probably don’t need to do the number crunching yourself (hallelujah!) but you do need to correctly understand and interpret the analysis created by your colleagues. One of the most important types of data analysis is called regression analysis.

• Amy Gallo is a contributing editor at Harvard Business Review, cohost of the Women at Work podcast , and the author of two books: Getting Along: How to Work with Anyone (Even Difficult People) and the HBR Guide to Dealing with Conflict . She writes and speaks about workplace dynamics. Watch her TEDx talk on conflict and follow her on LinkedIn . amyegallo

Partner Center

Regression Analysis in Market Research

by Richard Nehrboss SR | Mar 14, 2023 | Customer Experience Management , Financial Services , Research Methodology

What is Regression Analysis & How Is It Used?

Regression analysis helps organizations make sense of priority areas and what factors have the most impact and influence on their customer relationships. It allows researchers and brands to read between the lines of the survey data. This article will help you understand the definition of regression analysis, how it is commonly used, and the benefits of using regression research.

Regression Analysis: Definition

Regression analysis is a common statistical method that helps organizations understand the relationship between independent variables and dependent variables.

• Dependent variable: The main factor you want to measure or understand.
• Independent variables: The secondary factors you believe to have an influence on your dependent variable.

More specifically regression analysis tells you what factors are most important, which to disregard, and how each factor affects one another.

Importance of Regression Analysis

There are several benefits of regression analysis, most of which center around using it to achieve data-driven decision-making.

The advantages of using regression analysis in research include:

• Great tool for forecasting: While there is no such thing as a magic crystal ball, regression research is a great approach to measuring predictive analytics and forecasting.
• Focus attention on priority areas of improvement: Regression statistical analysis helps businesses and organizations prioritize efforts to improve customer satisfaction metrics such as net promoter score, customer effort score, and customer loyalty. Using regression analysis in quantitative research provides the opportunity to take corrective actions on the items that will most positively improve overall satisfaction.

When to Use Regression Analysis

A common use of regression analysis is understanding how the likelihood to recommend a product or service (dependent variable) is impacted by changes in wait time, price, and quantity purchased (presumably independent variables). A popular way to measure this is with net promoter score (NPS) as it is one of the most commonly used metrics in market research.

Net promoter score formula

The score is very telling to help your business understand how many raving fans your brand has in comparison to your key competitors and industry benchmarks. While our online survey company always recommends using an open-ended question after NPS to gather context to help understand the driving forces behind the score, sometimes it does not tell the whole story.

Regression Analysis Example in Business

Keeping with the bank survey from above, let’s say in the same survey you ask a series of customer satisfaction questions related to respondents’ experience with the bank. You believe the interest rates and customer service are good at your bank but you think there might be some underlying drivers really pushing your high NPS. In this example, likelihood to recommend, or NPS is your dependent variable A. Your more specific follow-up satisfaction questions are dependent variables B, C, D, E, F, G.

Through your regression analysis, you find out that INDEPENDENT VARIABLE C (friendliness of the staff) has the most significant effect on NPS. This means how the customer rates the friendliness of the staff members will have the largest overall impact on how likely they would be to recommend your bank. This is much different than what customers said in the open-ended comment about interest rates and customer service. However, as regression analysis proves, staff friendliness is essential.

Regression analysis is another tool market research firms used on a daily basis with their clients to help brands understand survey data from customers. The benefit of using a third-party market research firm is that you can leverage their expertise to tell you the “so what” of your customer survey data.

At The MSR Group, we use regression analysis to help our clients understand the relationship between independent variables and dependent variables. We have worked with banks to understand the impact that key index scores from the markets had on sales projections. We also help our clients prioritize efforts to improve customer satisfaction metrics such as net promoter score, customer effort score, and customer loyalty.

If you are interested in using regression analysis to help your business make data-driven decisions, contact The MSR Group by filling out an online contact form or emailing [email protected]. Regression analysis is a powerful tool that can help executives and management make data-driven decisions. It can help them understand the relationship between independent variables and dependent variables, and how each factor affects one another. It can also help them focus their attention on priority areas of improvement, and use predictive analytics and forecasting to understand how their revenue might be impacted in future quarters.

At The MSR Group, we use regression analysis to help our clients understand the relationship between independent variables and dependent variables, and prioritize efforts to improve customer satisfaction metrics. We have worked with banks to understand the impact that key index scores from the markets had on sales projections, and how increasing prices will have any impact on repeat customer purchases. Using regression analysis in quantitative research provides the opportunity to take corrective actions on the items that will most positively improve overall satisfaction.

Subscribe To Our Newsletter

Join our mailing list so you never miss an update from The MSR Group!

Thanks for subscribing!

• Customer Experience Management
• Employee Experience
• Financial Services
• Marketing Effectiveness
• News Releases
• Research Methodology
• Social Media
• Technology & Innovation

Join our email list to receive MSR Group news and industry updates right to your inbox!

You have Successfully Subscribed!

Regression analysis: Precise Forecasts and Predictions

Appinio Research · 03.07.2023 · 8min read

Back to Market Research Blog

Regression analysis plays a vital role in contemporary market research, offering a powerful tool for making accurate forecasts and addressing intricate interdependencies within challenges and decisions. It enables us to predict user behavior and gain valuable insights for optimizing business strategies. This article aims to elucidate the concept of regression analysis, delve into its working principles, and explore its applications in the field of market research.

What is regression analysis?

Regression analysis serves as a statistical method and acts as a translator within the realm of market research, enabling the conversion of ambiguous or complex data into concise and understandable information.

By investigating the relationship between two or more variables, regression analysis sheds light on crucial interactions, such as the correlation between user behavior and screen time in smartphone applications.

What does regression analysis do?

Regression analysis serves multiple purposes. 

• It identifies correlations between two or more variables, allowing us to understand and visualize their interrelationship.
• It has the capability to forecast potential changes when variables are altered.
• It can capture values at specific time points, enabling us to examine the impact of fluctuating parameters on the overall outcomes.

Origins of Regression Analysis

Regression analysis traces its roots back to the late 19th century when it was pioneered by the renowned British statistician, Sir Francis Galton. Galton explored variables within human genetics and introduced the concept of regression.

By examining the relationship between parental height and the height of their offspring, Galton laid the foundation for linear regression analysis. Since then, this methodology has found extensive applications not only in market research but also in diverse fields such as psychology, sociology, medicine, and economics.

Precise market analyses with Appinio

Appinio leverages a variety of market research methods to get you the best results for your market research needs. Do you want to determine the potential of a new product or service before launching it onto the market? Then the TURF analysis can help. 

Conjoint analysis, on the other hand, collects consumer feedback during the development phase to optimize an idea. 

Contact Appinio now and together we will find the optimal approach to your challenge!

What types of regression analysis are there?

Regression analysis encompasses various regression models, each serving specific purposes depending on the research objectives and data availability. 

Employing a combination of these techniques allows for in-depth insights into complex phenomena. Here are the key regression models:

Simple linear regression

The classic model examines the relationship between a dependent variable and a single independent variable, revealing their association. For instance, it can explore how daily coffee consumption (independent variable) impacts daily energy levels (dependent variable).

Multiple linear regression

Expanding upon simple linear regression, this model incorporates multiple independent variables, such as price, advertising, competition, or sales figures. In the context of energy levels, variables like sleep duration and exercise can be added alongside coffee consumption.

Non-linear regression

When the relationship between variables deviates from a straight line, non-linear regression comes into play. This is particularly useful for phenomena like exponential growth in app downloads or user numbers, where traditional linear models may not be suitable.

Quadratic regression

For complex correlations or patterns characterized by ups and downs, quadratic regression is utilized. 

It fits data that follows non-linear trends, such as seasonal sales fluctuations. For instance, it can help determine market saturation points, where growth typically plateaus after an initial rapid expansion.

Hierarchical regression 

Hierarchical regression allows the researcher to control the order of variables in a model, enabling the assessment of each independent variable's contribution to predicting the dependent variable. 

For example, in demographic-based analyses, variables like age, gender or education levels may be weighted differently.

Multinomial logistic regression

This model examines the probabilities of outcomes with more than two variables, making it valuable for complex questions. 

For instance, a music app may predict users' favorite genres based on their previous preferences, listening habits, and other factors like age, gender, or listening time, enabling personalized recommendations.

Multivariate regression analysis

When multiple dependent variables and their interactions with independent variables need to be explored, multivariate regression analysis is employed. 

For instance, in the context of fitness data, it can assess how factors such as diet, sleep, or exercise intensity influence variables like weight and health status.

Binary logistic regression

This model comes into play when a variable has only two possible answers, such as yes or no. Binary logistic regression can be utilized to predict whether a specific product will be purchased by a target group. Factors like age, income, or gender can further segment the buyer groups.

How is regression analysis used in market research?

The versatility of regression analysis is reflected in its diverse applications within the field of market research . Here are selected examples of how regression analysis is utilized:

• Predicting market trends Regression analysis enables the exploration of future market trends. For instance, a real estate company can forecast future home prices by considering factors such as property location, size, and age of the property. Similarly, a food company may employ regression analysis to identify the ice cream flavor with the highest sales potential.
• Customer satisfaction Companies can employ regression analysis to investigate the factors influencing customer satisfaction. By conducting customer surveys and analyzing the data through regression analysis, a customer service company can identify the aspects of their service that have the greatest impact on customer satisfaction.
• Usage behavior Regression analysis provides insights into the factors influencing the usage of smartphone apps. It allows for differentiation based on variables such as age, gender, or education level, shedding light on the drivers of app usage.
• Advertising impact Regression analysis measures the effectiveness of advertising campaigns. By analyzing advertising expenditure in relation to product sales, it enables the classification of advertising effectiveness and informs decision-making regarding advertising strategies.
• Measuring market maturity Regression analysis helps evaluate the reception of a product or service among the target audience. It identifies positive and negative evaluations, as well as determining which features should be emphasized. Through regression analyses, insights can be gained into products and services even before their market launch.

How does a simple linear regression analysis work?

Suppose a company aims to determine the relationship between advertising spending and product sales, requiring a simple linear regression analysis. Here are five possible steps to conduct this analysis:

• Data collection To commence the analysis, data on advertising spending and product sales needs to be collected.
• Chart generation The data is plotted on a scatter plot where one axis represents advertising spending and the other represents product sales.
• Determine the regression line A straight line is drawn to intersect as many data points as possible. This regression line illustrates the average relationship between the two variables.
• Predicting developments The regression line serves as the foundation for making future predictions. By manipulating one variable, you can examine its influence on the other variable.
• Interpretation of the results Valuable insights can be derived from the results. For instance, the analysis may reveal that an additional $10,000 in advertising spending could lead to an average increase in sales of 500 units.

Regression analysis: All-rounder in market research

Regression analysis stands as a powerful and versatile tool in the realm of market research. It offers a range of regression models, varying in complexity depending on the research question or objective at hand. Whether investigating the relationship between advertising spend and sales, analyzing usage behavior, or identifying market trends, regression analysis provides data-driven insights that empower informed and sound decision-making. 

Interested in running your own regression analysis?

Then register directly on our platform and get in touch with our experts.

Join the loop 💌

Be the first to hear about new updates, product news, and data insights. We'll send it all straight to your inbox.

Get the latest market research news straight to your inbox! 💌

Wait, there's more

30.05.2024 | 29min read

Pareto Analysis: Definition, Pareto Chart, Examples

28.05.2024 | 32min read

What is Systematic Sampling? Definition, Types, Examples

16.05.2024 | 30min read

Time Series Analysis: Definition, Types, Techniques, Examples

• Privacy Policy

Home » Regression Analysis – Methods, Types and Examples

Regression Analysis – Methods, Types and Examples

Table of Contents

Regression Analysis

Regression analysis is a set of statistical processes for estimating the relationships among variables . It includes many techniques for modeling and analyzing several variables when the focus is on the relationship between a dependent variable and one or more independent variables (or ‘predictors’).

Regression Analysis Methodology

Here is a general methodology for performing regression analysis:

• Define the research question: Clearly state the research question or hypothesis you want to investigate. Identify the dependent variable (also called the response variable or outcome variable) and the independent variables (also called predictor variables or explanatory variables) that you believe are related to the dependent variable.
• Collect data: Gather the data for the dependent variable and independent variables. Ensure that the data is relevant, accurate, and representative of the population or phenomenon you are studying.
• Explore the data: Perform exploratory data analysis to understand the characteristics of the data, identify any missing values or outliers, and assess the relationships between variables through scatter plots, histograms, or summary statistics.
• Choose the regression model: Select an appropriate regression model based on the nature of the variables and the research question. Common regression models include linear regression, multiple regression, logistic regression, polynomial regression, and time series regression, among others.
• Assess assumptions: Check the assumptions of the regression model. Some common assumptions include linearity (the relationship between variables is linear), independence of errors, homoscedasticity (constant variance of errors), and normality of errors. Violation of these assumptions may require additional steps or alternative models.
• Estimate the model: Use a suitable method to estimate the parameters of the regression model. The most common method is ordinary least squares (OLS), which minimizes the sum of squared differences between the observed and predicted values of the dependent variable.
• I nterpret the results: Analyze the estimated coefficients, p-values, confidence intervals, and goodness-of-fit measures (e.g., R-squared) to interpret the results. Determine the significance and direction of the relationships between the independent variables and the dependent variable.
• Evaluate model performance: Assess the overall performance of the regression model using appropriate measures, such as R-squared, adjusted R-squared, and root mean squared error (RMSE). These measures indicate how well the model fits the data and how much of the variation in the dependent variable is explained by the independent variables.
• Test assumptions and diagnose problems: Check the residuals (the differences between observed and predicted values) for any patterns or deviations from assumptions. Conduct diagnostic tests, such as examining residual plots, testing for multicollinearity among independent variables, and assessing heteroscedasticity or autocorrelation, if applicable.
• Make predictions and draw conclusions: Once you have a satisfactory model, use it to make predictions on new or unseen data. Draw conclusions based on the results of the analysis, considering the limitations and potential implications of the findings.

Types of Regression Analysis

Types of Regression Analysis are as follows:

Linear Regression

Linear regression is the most basic and widely used form of regression analysis. It models the linear relationship between a dependent variable and one or more independent variables. The goal is to find the best-fitting line that minimizes the sum of squared differences between observed and predicted values.

Multiple Regression

Multiple regression extends linear regression by incorporating two or more independent variables to predict the dependent variable. It allows for examining the simultaneous effects of multiple predictors on the outcome variable.

Polynomial Regression

Polynomial regression models non-linear relationships between variables by adding polynomial terms (e.g., squared or cubic terms) to the regression equation. It can capture curved or nonlinear patterns in the data.

Logistic Regression

Logistic regression is used when the dependent variable is binary or categorical. It models the probability of the occurrence of a certain event or outcome based on the independent variables. Logistic regression estimates the coefficients using the logistic function, which transforms the linear combination of predictors into a probability.

Ridge Regression and Lasso Regression

Ridge regression and Lasso regression are techniques used for addressing multicollinearity (high correlation between independent variables) and variable selection. Both methods introduce a penalty term to the regression equation to shrink or eliminate less important variables. Ridge regression uses L2 regularization, while Lasso regression uses L1 regularization.

Time Series Regression

Time series regression analyzes the relationship between a dependent variable and independent variables when the data is collected over time. It accounts for autocorrelation and trends in the data and is used in forecasting and studying temporal relationships.

Nonlinear Regression

Nonlinear regression models are used when the relationship between the dependent variable and independent variables is not linear. These models can take various functional forms and require estimation techniques different from those used in linear regression.

Poisson Regression

Poisson regression is employed when the dependent variable represents count data. It models the relationship between the independent variables and the expected count, assuming a Poisson distribution for the dependent variable.

Generalized Linear Models (GLM)

GLMs are a flexible class of regression models that extend the linear regression framework to handle different types of dependent variables, including binary, count, and continuous variables. GLMs incorporate various probability distributions and link functions.

Regression Analysis Formulas

Regression analysis involves estimating the parameters of a regression model to describe the relationship between the dependent variable (Y) and one or more independent variables (X). Here are the basic formulas for linear regression, multiple regression, and logistic regression:

Linear Regression:

Simple Linear Regression Model: Y = β0 + β1X + ε

Multiple Linear Regression Model: Y = β0 + β1X1 + β2X2 + … + βnXn + ε

In both formulas:

• Y represents the dependent variable (response variable).
• X represents the independent variable(s) (predictor variable(s)).
• β0, β1, β2, …, βn are the regression coefficients or parameters that need to be estimated.
• ε represents the error term or residual (the difference between the observed and predicted values).

Multiple Regression:

Multiple regression extends the concept of simple linear regression by including multiple independent variables.

Multiple Regression Model: Y = β0 + β1X1 + β2X2 + … + βnXn + ε

The formulas are similar to those in linear regression, with the addition of more independent variables.

Logistic Regression:

Logistic regression is used when the dependent variable is binary or categorical. The logistic regression model applies a logistic or sigmoid function to the linear combination of the independent variables.

Logistic Regression Model: p = 1 / (1 + e^-(β0 + β1X1 + β2X2 + … + βnXn))

In the formula:

• p represents the probability of the event occurring (e.g., the probability of success or belonging to a certain category).
• X1, X2, …, Xn represent the independent variables.
• e is the base of the natural logarithm.

The logistic function ensures that the predicted probabilities lie between 0 and 1, allowing for binary classification.

Regression Analysis Examples

Regression Analysis Examples are as follows:

• Stock Market Prediction: Regression analysis can be used to predict stock prices based on various factors such as historical prices, trading volume, news sentiment, and economic indicators. Traders and investors can use this analysis to make informed decisions about buying or selling stocks.
• Demand Forecasting: In retail and e-commerce, real-time It can help forecast demand for products. By analyzing historical sales data along with real-time data such as website traffic, promotional activities, and market trends, businesses can adjust their inventory levels and production schedules to meet customer demand more effectively.
• Energy Load Forecasting: Utility companies often use real-time regression analysis to forecast electricity demand. By analyzing historical energy consumption data, weather conditions, and other relevant factors, they can predict future energy loads. This information helps them optimize power generation and distribution, ensuring a stable and efficient energy supply.
• Online Advertising Performance: It can be used to assess the performance of online advertising campaigns. By analyzing real-time data on ad impressions, click-through rates, conversion rates, and other metrics, advertisers can adjust their targeting, messaging, and ad placement strategies to maximize their return on investment.
• Predictive Maintenance: Regression analysis can be applied to predict equipment failures or maintenance needs. By continuously monitoring sensor data from machines or vehicles, regression models can identify patterns or anomalies that indicate potential failures. This enables proactive maintenance, reducing downtime and optimizing maintenance schedules.
• Financial Risk Assessment: Real-time regression analysis can help financial institutions assess the risk associated with lending or investment decisions. By analyzing real-time data on factors such as borrower financials, market conditions, and macroeconomic indicators, regression models can estimate the likelihood of default or assess the risk-return tradeoff for investment portfolios.

Importance of Regression Analysis

Importance of Regression Analysis is as follows:

• Relationship Identification: Regression analysis helps in identifying and quantifying the relationship between a dependent variable and one or more independent variables. It allows us to determine how changes in independent variables impact the dependent variable. This information is crucial for decision-making, planning, and forecasting.
• Prediction and Forecasting: Regression analysis enables us to make predictions and forecasts based on the relationships identified. By estimating the values of the dependent variable using known values of independent variables, regression models can provide valuable insights into future outcomes. This is particularly useful in business, economics, finance, and other fields where forecasting is vital for planning and strategy development.
• Causality Assessment: While correlation does not imply causation, regression analysis provides a framework for assessing causality by considering the direction and strength of the relationship between variables. It allows researchers to control for other factors and assess the impact of a specific independent variable on the dependent variable. This helps in determining the causal effect and identifying significant factors that influence outcomes.
• Model Building and Variable Selection: Regression analysis aids in model building by determining the most appropriate functional form of the relationship between variables. It helps researchers select relevant independent variables and eliminate irrelevant ones, reducing complexity and improving model accuracy. This process is crucial for creating robust and interpretable models.
• Hypothesis Testing: Regression analysis provides a statistical framework for hypothesis testing. Researchers can test the significance of individual coefficients, assess the overall model fit, and determine if the relationship between variables is statistically significant. This allows for rigorous analysis and validation of research hypotheses.
• Policy Evaluation and Decision-Making: Regression analysis plays a vital role in policy evaluation and decision-making processes. By analyzing historical data, researchers can evaluate the effectiveness of policy interventions and identify the key factors contributing to certain outcomes. This information helps policymakers make informed decisions, allocate resources effectively, and optimize policy implementation.
• Risk Assessment and Control: Regression analysis can be used for risk assessment and control purposes. By analyzing historical data, organizations can identify risk factors and develop models that predict the likelihood of certain outcomes, such as defaults, accidents, or failures. This enables proactive risk management, allowing organizations to take preventive measures and mitigate potential risks.

When to Use Regression Analysis

• Prediction : Regression analysis is often employed to predict the value of the dependent variable based on the values of independent variables. For example, you might use regression to predict sales based on advertising expenditure, or to predict a student’s academic performance based on variables like study time, attendance, and previous grades.
• Relationship analysis: Regression can help determine the strength and direction of the relationship between variables. It can be used to examine whether there is a linear association between variables, identify which independent variables have a significant impact on the dependent variable, and quantify the magnitude of those effects.
• Causal inference: Regression analysis can be used to explore cause-and-effect relationships by controlling for other variables. For example, in a medical study, you might use regression to determine the impact of a specific treatment while accounting for other factors like age, gender, and lifestyle.
• Forecasting : Regression models can be utilized to forecast future trends or outcomes. By fitting a regression model to historical data, you can make predictions about future values of the dependent variable based on changes in the independent variables.
• Model evaluation: Regression analysis can be used to evaluate the performance of a model or test the significance of variables. You can assess how well the model fits the data, determine if additional variables improve the model’s predictive power, or test the statistical significance of coefficients.
• Data exploration : Regression analysis can help uncover patterns and insights in the data. By examining the relationships between variables, you can gain a deeper understanding of the data set and identify potential patterns, outliers, or influential observations.

Applications of Regression Analysis

Here are some common applications of regression analysis:

• Economic Forecasting: Regression analysis is frequently employed in economics to forecast variables such as GDP growth, inflation rates, or stock market performance. By analyzing historical data and identifying the underlying relationships, economists can make predictions about future economic conditions.
• Financial Analysis: Regression analysis plays a crucial role in financial analysis, such as predicting stock prices or evaluating the impact of financial factors on company performance. It helps analysts understand how variables like interest rates, company earnings, or market indices influence financial outcomes.
• Marketing Research: Regression analysis helps marketers understand consumer behavior and make data-driven decisions. It can be used to predict sales based on advertising expenditures, pricing strategies, or demographic variables. Regression models provide insights into which marketing efforts are most effective and help optimize marketing campaigns.
• Health Sciences: Regression analysis is extensively used in medical research and public health studies. It helps examine the relationship between risk factors and health outcomes, such as the impact of smoking on lung cancer or the relationship between diet and heart disease. Regression analysis also helps in predicting health outcomes based on various factors like age, genetic markers, or lifestyle choices.
• Social Sciences: Regression analysis is widely used in social sciences like sociology, psychology, and education research. Researchers can investigate the impact of variables like income, education level, or social factors on various outcomes such as crime rates, academic performance, or job satisfaction.
• Operations Research: Regression analysis is applied in operations research to optimize processes and improve efficiency. For example, it can be used to predict demand based on historical sales data, determine the factors influencing production output, or optimize supply chain logistics.
• Environmental Studies: Regression analysis helps in understanding and predicting environmental phenomena. It can be used to analyze the impact of factors like temperature, pollution levels, or land use patterns on phenomena such as species diversity, water quality, or climate change.
• Sports Analytics: Regression analysis is increasingly used in sports analytics to gain insights into player performance, team strategies, and game outcomes. It helps analyze the relationship between various factors like player statistics, coaching strategies, or environmental conditions and their impact on game outcomes.

Advantages and Disadvantages of Regression Analysis

About the author.

Muhammad Hassan

Researcher, Academic Writer, Web developer

You may also like

Bimodal Histogram – Definition, Examples

Textual Analysis – Types, Examples and Guide

Probability Histogram – Definition, Examples and...

Discriminant Analysis – Methods, Types and...

Cluster Analysis – Types, Methods and Examples

Content Analysis – Methods, Types and Examples

• Skip to main content
• Skip to primary sidebar
• Skip to footer
• QuestionPro

• Solutions Industries Gaming Automotive Sports and events Education Government Travel & Hospitality Financial Services Healthcare Cannabis Technology Use Case NPS+ Communities Audience Contactless surveys Mobile LivePolls Member Experience GDPR Positive People Science 360 Feedback Surveys
• Resources Blog eBooks Survey Templates Case Studies Training Help center

Home Market Research

Regression Analysis: Definition, Types, Usage & Advantages

Regression analysis is perhaps one of the most widely used statistical methods for investigating or estimating the relationship between a set of independent and dependent variables. In statistical analysis , distinguishing between categorical data and numerical data is essential, as categorical data involves distinct categories or labels, while numerical data consists of measurable quantities.

It is also used as a blanket term for various data analysis techniques utilized in a qualitative research method for modeling and analyzing numerous variables. In the regression method, the dependent variable is a predictor or an explanatory element, and the dependent variable is the outcome or a response to a specific query.

LEARN ABOUT:   Statistical Analysis Methods

Content Index

Definition of Regression Analysis

Types of regression analysis, regression analysis usage in market research, how regression analysis derives insights from surveys, advantages of using regression analysis in an online survey.

Regression analysis is often used to model or analyze data. Most survey analysts use it to understand the relationship between the variables, which can be further utilized to predict the precise outcome.

For Example – Suppose a soft drink company wants to expand its manufacturing unit to a newer location. Before moving forward, the company wants to analyze its revenue generation model and the various factors that might impact it. Hence, the company conducts an online survey with a specific questionnaire.

After using regression analysis, it becomes easier for the company to analyze the survey results and understand the relationship between different variables like electricity and revenue – here, revenue is the dependent variable.

LEARN ABOUT: Level of Analysis

In addition, understanding the relationship between different independent variables like pricing, number of workers, and logistics with the revenue helps the company estimate the impact of varied factors on sales and profits.

Survey researchers often use this technique to examine and find a correlation between different variables of interest. It provides an opportunity to gauge the influence of different independent variables on a dependent variable.

Overall, regression analysis saves the survey researchers’ additional efforts in arranging several independent variables in tables and testing or calculating their effect on a dependent variable. Different types of analytical research methods are widely used to evaluate new business ideas and make informed decisions.

Create a Free Account

Researchers usually start by learning linear and logistic regression first. Due to the widespread knowledge of these two methods and ease of application, many analysts think there are only two types of models. Each model has its own specialty and ability to perform if specific conditions are met.

This blog explains the commonly used seven types of multiple regression analysis methods that can be used to interpret the enumerated data in various formats.

01. Linear Regression Analysis

It is one of the most widely known modeling techniques, as it is amongst the first elite regression analysis methods picked up by people at the time of learning predictive modeling. Here, the dependent variable is continuous, and the independent variable is more often continuous or discreet with a linear regression line.

Please note that multiple linear regression has more than one independent variable than simple linear regression. Thus, linear regression is best to be used only when there is a linear relationship between the independent and a dependent variable.

A business can use linear regression to measure the effectiveness of the marketing campaigns, pricing, and promotions on sales of a product. Suppose a company selling sports equipment wants to understand if the funds they have invested in the marketing and branding of their products have given them substantial returns or not.

Linear regression is the best statistical method to interpret the results. The best thing about linear regression is it also helps in analyzing the obscure impact of each marketing and branding activity, yet controlling the constituent’s potential to regulate the sales.

If the company is running two or more advertising campaigns simultaneously, one on television and two on radio, then linear regression can easily analyze the independent and combined influence of running these advertisements together.

LEARN ABOUT: Data Analytics Projects

02. Logistic Regression Analysis

Logistic regression is commonly used to determine the probability of event success and event failure. Logistic regression is used whenever the dependent variable is binary, like 0/1, True/False, or Yes/No. Thus, it can be said that logistic regression is used to analyze either the close-ended questions in a survey or the questions demanding numeric responses in a survey.

Please note logistic regression does not need a linear relationship between a dependent and an independent variable, just like linear regression. Logistic regression applies a non-linear log transformation for predicting the odds ratio; therefore, it easily handles various types of relationships between a dependent and an independent variable.

Logistic regression is widely used to analyze categorical data, particularly for binary response data in business data modeling. More often, logistic regression is used when the dependent variable is categorical, like to predict whether the health claim made by a person is real(1) or fraudulent, to understand if the tumor is malignant(1) or not.

Businesses use logistic regression to predict whether the consumers in a particular demographic will purchase their product or will buy from the competitors based on age, income, gender, race, state of residence, previous purchase, etc.

03. Polynomial Regression Analysis

Polynomial regression is commonly used to analyze curvilinear data when an independent variable’s power is more than 1. In this regression analysis method, the best-fit line is never a ‘straight line’ but always a ‘curve line’ fitting into the data points.

Please note that polynomial regression is better to use when two or more variables have exponents and a few do not.

Additionally, it can model non-linearly separable data offering the liberty to choose the exact exponent for each variable, and that too with full control over the modeling features available.

When combined with response surface analysis, polynomial regression is considered one of the sophisticated statistical methods commonly used in multisource feedback research. Polynomial regression is used mostly in finance and insurance-related industries where the relationship between dependent and independent variables is curvilinear.

Suppose a person wants to budget expense planning by determining how long it would take to earn a definitive sum. Polynomial regression, by taking into account his/her income and predicting expenses, can easily determine the precise time he/she needs to work to earn that specific sum amount.

04. Stepwise Regression Analysis

This is a semi-automated process with which a statistical model is built either by adding or removing the dependent variable on the t-statistics of their estimated coefficients.

If used properly, the stepwise regression will provide you with more powerful data at your fingertips than any method. It works well when you are working with a large number of independent variables. It just fine-tunes the unit of analysis model by poking variables randomly.

Stepwise regression analysis is recommended to be used when there are multiple independent variables, wherein the selection of independent variables is done automatically without human intervention.

Please note, in stepwise regression modeling, the variable is added or subtracted from the set of explanatory variables. The set of added or removed variables is chosen depending on the test statistics of the estimated coefficient.

Suppose you have a set of independent variables like age, weight, body surface area, duration of hypertension, basal pulse, and stress index based on which you want to analyze its impact on the blood pressure.

In stepwise regression, the best subset of the independent variable is automatically chosen; it either starts by choosing no variable to proceed further (as it adds one variable at a time) or starts with all variables in the model and proceeds backward (removes one variable at a time).

Thus, using regression analysis, you can calculate the impact of each or a group of variables on blood pressure.

05. Ridge Regression Analysis

Ridge regression is based on an ordinary least square method which is used to analyze multicollinearity data (data where independent variables are highly correlated). Collinearity can be explained as a near-linear relationship between variables.

Whenever there is multicollinearity, the estimates of least squares will be unbiased, but if the difference between them is larger, then it may be far away from the true value. However, ridge regression eliminates the standard errors by appending some degree of bias to the regression estimates with a motive to provide more reliable estimates.

If you want, you can also learn about Selection Bias through our blog.

Please note, Assumptions derived through the ridge regression are similar to the least squared regression, the only difference being the normality. Although the value of the coefficient is constricted in the ridge regression, it never reaches zero suggesting the inability to select variables.

Suppose you are crazy about two guitarists performing live at an event near you, and you go to watch their performance with a motive to find out who is a better guitarist. But when the performance starts, you notice that both are playing black-and-blue notes at the same time.

Is it possible to find out the best guitarist having the biggest impact on sound among them when they are both playing loud and fast? As both of them are playing different notes, it is substantially difficult to differentiate them, making it the best case of multicollinearity, which tends to increase the standard errors of the coefficients.

Ridge regression addresses multicollinearity in cases like these and includes bias or a shrinkage estimation to derive results.

06. Lasso Regression Analysis

Lasso (Least Absolute Shrinkage and Selection Operator) is similar to ridge regression; however, it uses an absolute value bias instead of the square bias used in ridge regression.

It was developed way back in 1989 as an alternative to the traditional least-squares estimate with the intention to deduce the majority of problems related to overfitting when the data has a large number of independent variables.

Lasso has the capability to perform both – selecting variables and regularizing them along with a soft threshold. Applying lasso regression makes it easier to derive a subset of predictors from minimizing prediction errors while analyzing a quantitative response.

Please note that regression coefficients reaching zero value after shrinkage are excluded from the lasso model. On the contrary, regression coefficients having more value than zero are strongly associated with the response variables, wherein the explanatory variables can be either quantitative, categorical, or both.

Suppose an automobile company wants to perform a research analysis on average fuel consumption by cars in the US. For samples, they chose 32 models of car and 10 features of automobile design – Number of cylinders, Displacement, Gross horsepower, Rear axle ratio, Weight, ¼ mile time, v/s engine, transmission, number of gears, and number of carburetors.

As you can see a correlation between the response variable mpg (miles per gallon) is extremely correlated to some variables like weight, displacement, number of cylinders, and horsepower. The problem can be analyzed by using the glmnet package in R and lasso regression for feature selection.

07. Elastic Net Regression Analysis

It is a mixture of ridge and lasso regression models trained with L1 and L2 norms. The elastic net brings about a grouping effect wherein strongly correlated predictors tend to be in/out of the model together. Using the elastic net regression model is recommended when the number of predictors is far greater than the number of observations.

Please note that the elastic net regression model came into existence as an option to the lasso regression model as lasso’s variable section was too much dependent on data, making it unstable. By using elastic net regression, statisticians became capable of over-bridging the penalties of ridge and lasso regression only to get the best out of both models.

A clinical research team having access to a microarray data set on leukemia (LEU) was interested in constructing a diagnostic rule based on the expression level of presented gene samples for predicting the type of leukemia. The data set they had, consisted of a large number of genes and a few samples.

Apart from that, they were given a specific set of samples to be used as training samples, out of which some were infected with type 1 leukemia (acute lymphoblastic leukemia) and some with type 2 leukemia (acute myeloid leukemia).

Model fitting and tuning parameter selection by tenfold CV were carried out on the training data. Then they compared the performance of those methods by computing their prediction mean-squared error on the test data to get the necessary results.

A market research survey focuses on three major matrices; Customer Satisfaction , Customer Loyalty , and Customer Advocacy . Remember, although these matrices tell us about customer health and intentions, they fail to tell us ways of improving the position. Therefore, an in-depth survey questionnaire intended to ask consumers the reason behind their dissatisfaction is definitely a way to gain practical insights.

However, it has been found that people often struggle to put forth their motivation or demotivation or describe their satisfaction or dissatisfaction. In addition to that, people always give undue importance to some rational factors, such as price, packaging, etc. Overall, it acts as a predictive analytic and forecasting tool in market research.

When used as a forecasting tool, regression analysis can determine an organization’s sales figures by taking into account external market data. A multinational company conducts a market research survey to understand the impact of various factors such as GDP (Gross Domestic Product), CPI (Consumer Price Index), and other similar factors on its revenue generation model.

Obviously, regression analysis in consideration of forecasted marketing indicators was used to predict a tentative revenue that will be generated in future quarters and even in future years. However, the more forward you go in the future, the data will become more unreliable, leaving a wide margin of error .

Case study of using regression analysis

A water purifier company wanted to understand the factors leading to brand favorability. The survey was the best medium for reaching out to existing and prospective customers. A large-scale consumer survey was planned, and a discreet questionnaire was prepared using the best survey tool .

A number of questions related to the brand, favorability, satisfaction, and probable dissatisfaction were effectively asked in the survey. After getting optimum responses to the survey, regression analysis was used to narrow down the top ten factors responsible for driving brand favorability.

All the ten attributes derived (mentioned in the image below) in one or the other way highlighted their importance in impacting the favorability of that specific water purifier brand.

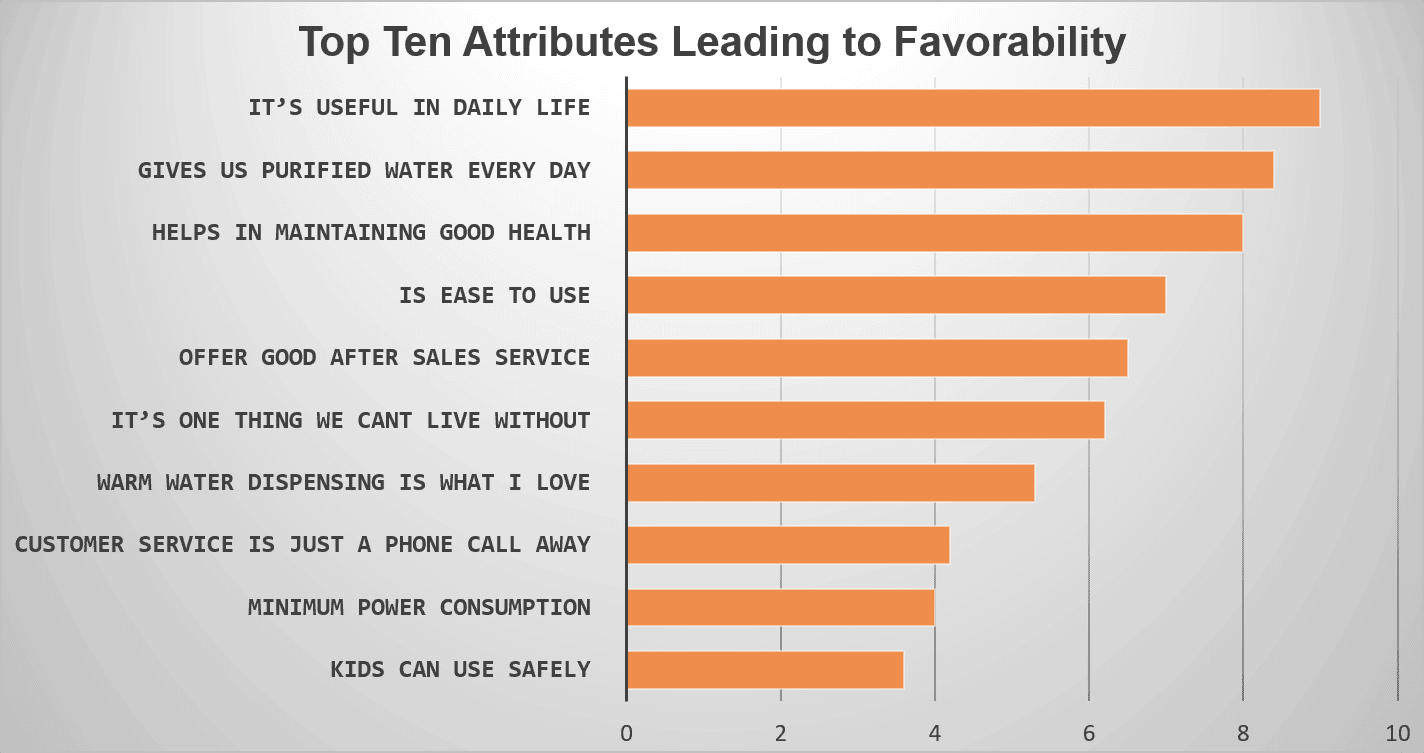
It is easy to run a regression analysis using Excel or SPSS, but while doing so, the importance of four numbers in interpreting the data must be understood.

The first two numbers out of the four numbers directly relate to the regression model itself.

• F-Value: It helps in measuring the statistical significance of the survey model. Remember, an F-Value significantly less than 0.05 is considered to be more meaningful. Less than 0.05 F-Value ensures survey analysis output is not by chance.
• R-Squared: This is the value wherein the independent variables try to explain the amount of movement by dependent variables. Considering the R-Squared value is 0.7, a tested independent variable can explain 70% of the dependent variable’s movement. It means the survey analysis output we will be getting is highly predictive in nature and can be considered accurate.

The other two numbers relate to each of the independent variables while interpreting regression analysis.

• P-Value: Like F-Value, even the P-Value is statistically significant. Moreover, here it indicates how relevant and statistically significant the independent variable’s effect is. Once again, we are looking for a value of less than 0.05.
• Interpretation: The fourth number relates to the coefficient achieved after measuring the impact of variables. For instance, we test multiple independent variables to get a coefficient. It tells us, ‘by what value the dependent variable is expected to increase when independent variables (which we are considering) increase by one when all other independent variables are stagnant at the same value.

In a few cases, the simple coefficient is replaced by a standardized coefficient demonstrating the contribution from each independent variable to move or bring about a change in the dependent variable.

01. Get access to predictive analytics

Do you know utilizing regression analysis to understand the outcome of a business survey is like having the power to unveil future opportunities and risks?

For example, after seeing a particular television advertisement slot, we can predict the exact number of businesses using that data to estimate a maximum bid for that slot. The finance and insurance industry as a whole depends a lot on regression analysis of survey data to identify trends and opportunities for more accurate planning and decision-making.

02. Enhance operational efficiency

Do you know businesses use regression analysis to optimize their business processes?

For example, before launching a new product line, businesses conduct consumer surveys to better understand the impact of various factors on the product’s production, packaging, distribution, and consumption.

A data-driven foresight helps eliminate the guesswork, hypothesis, and internal politics from decision-making. A deeper understanding of the areas impacting operational efficiencies and revenues leads to better business optimization.

03. Quantitative support for decision-making

Business surveys today generate a lot of data related to finance, revenue, operation, purchases, etc., and business owners are heavily dependent on various data analysis models to make informed business decisions.

For example, regression analysis helps enterprises to make informed strategic workforce decisions. Conducting and interpreting the outcome of employee surveys like Employee Engagement Surveys, Employee Satisfaction Surveys, Employer Improvement Surveys, Employee Exit Surveys, etc., boosts the understanding of the relationship between employees and the enterprise.

It also helps get a fair idea of certain issues impacting the organization’s working culture, working environment, and productivity. Furthermore, intelligent business-oriented interpretations reduce the huge pile of raw data into actionable information to make a more informed decision.

04. Prevent mistakes from happening due to intuitions

By knowing how to use regression analysis for interpreting survey results, one can easily provide factual support to management for making informed decisions. ; but do you know that it also helps in keeping out faults in the judgment?

For example, a mall manager thinks if he extends the closing time of the mall, then it will result in more sales. Regression analysis contradicts the belief that predicting increased revenue due to increased sales won’t support the increased operating expenses arising from longer working hours.

Regression analysis is a useful statistical method for modeling and comprehending the relationships between variables. It provides numerous advantages to various data types and interactions. Researchers and analysts may gain useful insights into the factors influencing a dependent variable and use the results to make informed decisions. 

With QuestionPro Research, you can improve the efficiency and accuracy of regression analysis by streamlining the data gathering, analysis, and reporting processes. The platform’s user-friendly interface and wide range of features make it a valuable tool for researchers and analysts conducting regression analysis as part of their research projects.

Sign up for the free trial today and let your research dreams fly!

FREE TRIAL         LEARN MORE

MORE LIKE THIS

Why Multilingual 360 Feedback Surveys Provide Better Insights

Jun 3, 2024

Raked Weighting: A Key Tool for Accurate Survey Results

May 31, 2024

Top 8 Data Trends to Understand the Future of Data

May 30, 2024

Top 12 Interactive Presentation Software to Engage Your User

May 29, 2024

Other categories

• Academic Research
• Artificial Intelligence
• Assessments
• Brand Awareness
• Case Studies
• Communities
• Consumer Insights
• Customer effort score
• Customer Engagement
• Customer Experience
• Customer Loyalty
• Customer Research
• Customer Satisfaction
• Employee Benefits
• Employee Engagement
• Employee Retention
• Friday Five
• General Data Protection Regulation
• Insights Hub
• Life@QuestionPro
• Market Research
• Mobile diaries
• Mobile Surveys
• New Features
• Online Communities
• Question Types
• Questionnaire
• QuestionPro Products
• Release Notes
• Research Tools and Apps
• Revenue at Risk
• Survey Templates
• Training Tips
• Uncategorized
• Video Learning Series
• What’s Coming Up
• Workforce Intelligence

How to Use a Regression Analysis for Marketing

Aristide Basque

Are you looking for an effective way to measure and analyze your marketing campaigns? Regression analysis might be your solution. It’s a powerful statistical method that can be invaluable for businesses looking to gain insights into their marketing strategies.

In other words, it enables marketers to identify relationships between variables, such as sales and advertising budgets or customer satisfaction and retention. By using this, you can determine which variables influence certain outcomes. With this information, marketers can adjust their strategies to be more aligned with their goals.

What is Regression Analysis?

Regression analysis is a statistical technique to study the relationship between two or more variable. Often used in marketing strategies, you can assess customer behavior and identify patterns helping marketing decisions.

• For example, marketers can use regression analysis to:
• Discover which demographic factors will lead to higher sales.
• Identify the best product placement for a particular demographic
• Determine which customers are more likely to become loyal repeat customers.

Furthermore, you can also use these analysis for other company functions, including data and machine learning. In Understanding Kernel Regression by BowTiedRaptor , we learn that you can even forecast future trends and estimate unknown functions of a random variables. It can prove ever useful to predict customer behaviors or financial results.

How to Use Regression Analysis for Marketing?

There are various ways you can use regression analysis in marketing. Here are a few of the most common:

• Identifying target audiences: identify the customer segments more likely to buy. You can identify them with your analysis, allowing you to focus and tailor your marketing messaging to drive the most sales.
• Predicting customer behavior: regression analysis can help predict customer buying patterns by studying different variables such as demographics, location, and purchase history. In turn, you can create targeted marketing strategies to increase your sales.
• Optimizing website conversion rates: by using regression analysis to study user behaviors on websites, you can optimize your website design and content to increase the conversion rate of visitors.
• Improving customer retention: by studying customer purchase patterns, regression analysis can help identify customers who are more likely to become loyal repeat customers. Afterwards, you can develop marketing strategies to keep those customers.
• Analyze if social engagement influences sales: analyze the correlation between social media engagement and sales. Doing that will help you understand which campaigns are most successful in driving revenue.
• Email marketing analysis: you can use regression analysis to measure the effectiveness of email campaigns, including click-through rates and open rates. With a stronger data, you can refine future campaigns enabling higher engagement and better results.
• Page authority and sales: you can determine the impact of your page authority on your sales by seeing if there’s any correlation between the two. This data can be used to optimize SEO and increase the visibility of your brand.
• If you’re located in Australia, you should definitely consider a local SEO expert to help you with this. Find the best AI Consultant Australia has to offer and start optimizing your online presence. Not only will this improve your sales, but it will also help you take advantage of the growing online market in Australia.

How to use it in your marketing

Before you start analyzing your marketing efforts, there are a few things you need to consider. These include:

• Choosing the right model: Selecting the right model is essential to getting accurate and reliable results. Different models are better suited for different types of data and applications, so choosing the best suited for your needs is important.
• Understanding correlation vs. causation: Regression analysis can be used to identify correlations between variables However, it’s important to note that correlation does not necessarily indicate causation.
• Utilizing expert help: if you’re unfamiliar with regression analysis, it’s best to enlist the help of an experienced analyst who can ensure the results are reliable and accurate.
• Including continuous and categorical variables: regression analysis can be used to model both continuous and categorical variables. Make sure you consider all the relevant variables when analyzing your data.
• Research before starting: before you start using regression analysis for marketing, it’s important to do your research and understand the basics. In other words, make sure your know what you’re doing!
• Use the simplest model possible: keep in mind that simpler models tend to yield more reliable results. Rather than trying to overcomplicate your analysis, focus on using the simplest model possible for each application.

Data-Driven Marketing: Regression to the Mean

Regression analysis is an essential tool for marketing professionals looking to optimize their efforts and better target potential customers. By understanding the correlation between independent and dependent variables, marketers can gain valuable insights into consumer behavior and how to best reach them with their campaigns.

This data-driven approach leads to more targeted campaigns with higher return on investment and improved customer engagement. With the right strategy, regression analysis can be a powerful tool for driving success in marketing. By utilizing this tool, marketers can make informed decisions that lead to more effective campaigns. Ultimately, it will help you drive better results for their business.

Get a free marketing proposal

Our proposal’s are full of creative marketing ideas you can leverage in your business. Everything we’ll share is based on our extensive experience & recent successes we’ve had.

Exclusive Facebook Ads Insights

Gain access to the most exclusive Facebook ads insights from our team of experts for free. Delivered every month, straight to your inbox.

Regression Analysis

• Home > What We Do > Research Methods > Pricing and Value Research Techniques > Regression Analysis

From overall customer satisfaction to satisfaction with your product quality and price, regression analysis measures the strength of a relationship between different variables.

Contact Us >

To find out more about measuring customer satisfaction to help your business

How regression analysis works

While correlation analysis provides a single numeric summary of a relation (“the correlation coefficient”), regression analysis results in a prediction equation, describing the relationship between the variables. If the relationship is strong – expressed by the Rsquare value – it can be used to predict values of one variable given the other variables have known values. For example, how will the overall satisfaction score change if satisfaction with product quality goes up from 6 to 7?

Measuring customer satisfaction

Regression analysis can be used in customer satisfaction and employee satisfaction studies to answer questions such as: “Which product dimensions contribute most to someone’s overall satisfaction or loyalty to the brand?” This is often referred to as Key Drivers Analysis.

It can also be used to simulate the outcome when actions are taken. For example: “What will happen to the satisfaction score when product availability is improved?”

Contact Us >  

Privacy Overview

Regression Analysis

Regression analysis is a quantitative research method which is used when the study involves modelling and analysing several variables, where the relationship includes a dependent variable and one or more independent variables. In simple terms, regression analysis is a quantitative method used to test the nature of relationships between a dependent variable and one or more independent variables.

The basic form of regression models includes unknown parameters (β), independent variables (X), and the dependent variable (Y).

Regression model, basically, specifies the relation of dependent variable (Y) to a function combination of independent variables (X) and unknown parameters (β)

                                    Y  ≈  f (X, β)   

Regression equation can be used to predict the values of ‘y’, if the value of ‘x’ is given, and both ‘y’ and ‘x’ are the two sets of measures of a sample size of ‘n’. The formulae for regression equation would be

Do not be intimidated by visual complexity of correlation and regression formulae above. You don’t have to apply the formula manually, and correlation and regression analyses can be run with the application of popular analytical software such as Microsoft Excel, Microsoft Access, SPSS and others.

Linear regression analysis is based on the following set of assumptions:

1. Assumption of linearity . There is a linear relationship between dependent and independent variables.

2. Assumption of homoscedasticity . Data values for dependent and independent variables have equal variances.

3. Assumption of absence of collinearity or multicollinearity . There is no correlation between two or more independent variables.

4. Assumption of normal distribution . The data for the independent variables and dependent variable are normally distributed

My e-book,  The Ultimate Guide to Writing a Dissertation in Business Studies: a step by step assistance  offers practical assistance to complete a dissertation with minimum or no stress. The e-book covers all stages of writing a dissertation starting from the selection to the research area to submitting the completed version of the work within the deadline. John Dudovskiy

Michael Pawlicki

Business Consulting

• About this Website
• About Michael Pawlicki
• Cluster Analysis
• Multidimensional Scaling
• Conjoint Analysis
• Choice Illusion
• Ebbinghaus Illusion
• Maslow’s Hierarchy of Needs
• Marketing Research
• Pricing Strategy
• Facebook 2020: $100 Billion Superstar or Failure
• Amazon Kindle Fire
• Marketing Plan for NHS

Regression Analysis – predicting the future

In marketing, the regression analysis is used to predict how the relationship between two variables, such as advertising and sales, can develop over time. Business managers can draw the regression line with data (cases) derived from historical sales data available to them.

The purpose of regression analysis is to describe, predict and control the relationship between at least two variables. The basic principle is to minimise the distance between the actual data and the perditions of the regression line. Regression analysis is used for variations in market share, sales and brand preference and this is normally done using variables such as advertising, price, distribution and quality.

•  Regression analysis is used:
•  To predict the values of the dependent variable
• To determine the independent variables
• To explain significant variation in the dependent variable and whether a relationship between variables exists
• To measure strength of the relationship
• To determine structure or form of the relationship

An online t-shirt sales company invested in Google AdWords advertising:

• £1000 in January
• £1000 in February
• £1000 in March

Their sales grew steadily in this period:

• £5000 in January
• £5500 in February
• £6000 in March

The managers can predict by looking at the regression line that with current level of advertising spent (£1000 per month) the sales in April will be £6500. This obviously would be the case if all other things remain equal but in reality they never do. The sales managers should use the prediction data from the regression analysis as an additional managerial tool but should not exclusively rely on it. The level of sales can be affected by elements other than the level of advertising. This includes, but is not limited to, factors such as weather conditions or the central bank’s increase or decrease of base interest rates. Regression analysis is concerned with the nature and degree of association between variables but does not assume causality (does not explain why there is relationship between variables). Other good examples of how regression analysis can be used to test marketing relevant hypothesis are: Can variation in demand be explained in terms of variation in fuel prices? Are consumers’ perceptions of quality determined by their perceptions in price? For a simple tutorial about the regression analysis for beginners please view the video below:

Regression analysis consists of number of statistics used to determine its accuracy and usefulness for certain purpose. Some of those statistics and methods are clearly explained by the statistics experts in the videos listed below. It is recommended that you read the text first and then watch the corresponding video:

• Product Moment Correlation (r) is a statistic summarising the strength of association between two metric variables (for example: X and Y). It is used to determine whether a linear (straight line) relationship exists between X and Y. It indicates the degree to which the variation in one variable (X) is related to the variation in another variable (Y) (also known as Pearson or Simple Correlation, Bivariate Correlation or Correlation Coefficient) . Covariance is a systematic relationship between two variables in which a change in one implies a corresponding change in the other (COV x Y).  The correlation coefficient between two variables will be the same regardless of their units of measurement. If r = 0.93 (a value close to 1.0) it means that one variable is strongly associated with the other. It does not matter which variable is considered dependent and which independent (X with Y) or (Y with X). The ‘r’ is designed to measure the strength of linear relationship, thus r= 0 does not suggest that there is no relationship between X and Y as there could be a non-linear relationship between the two.

• Residuals – the difference between the observed value of Y and the value predicted by the regression equation.

• Partial Correlation Coefficient – measures the association between the variables after adjusting for the effect of one or more additional variables. For example: how strongly related are sales to advertising expenditure when the effect of price is controlled?
• Part Correlation Coefficient – is a measure of the correlation between Y and X when the linear effects of the other independent variables have been removed from X but not from Y.
• Non-metric Correlation – a correlation measure for two non-metric variables that rely on rankings to compute the correlations.
• Least Squares Procedure – is a technique for fitting straight line to a scattergram by minimising the vertical distances of all the points from the line. The best fitting line is a regression line. The vertical distance from the point to the line is the error (e). read more
• Significance Testing – significance of the linear relationship between X and Y may be tested by examining two hypothesis:
• There is no linear relationship between X and Y
• There is a relationship (positive or negative) between X and Y

The strength and significance of association is measured by the coefficient of determination r-square (r2). Significance Testing involves testing the significance of the overall regression equation as well as specific partial regression coefficients.

Multiple Regression

Multiple Regression is extremely relevant to business analysis. Itinvolves single dependent variable such as sales and two or more independent variables such as employee remuneration, number of staff, level of advertising, online marketing spend. For example: can variation in sales be explained in terms of variation in advertising expenditures, prices and level of distribution? It is possible to consider additional independent variables to answer the question raised. Statistics relevant to multiple regression are: adjusted r-square (r2) – coefficient of multiple determination is adjusted for the number of independent variables and the sample size to account for diminishing returns. To get more insight into multiple regression and understand how other statistics such as significance testing influence the usefulness of the analysis please watch the video below:

References:

• Tuk, M., 2012. Regression Analysis, Marketing Analytics . Imperial College London, unpublished.
• Malhotra, K. N. and Birks, F.D., 2000. Marketing Research. An applied approach. European Edition . London: Pearson

Written by Michael Pawlicki

Speak Your Mind Cancel reply

About the author, recent posts.

• Price Elasticity
• Multidimensional Scaling (MDS) for Marketing
• Marketing Plan for Healthcare

Advertisements

• August 2015
• August 2014
• January 2013
• October 2012
• January 2012
• February 2010

Social Media

• Google Plus

Connect with Me

Return to top of page

Copyright © 2024 · eleven40 theme on Genesis Framework · WordPress · Log in

Forecasting e-commerce consumer returns: a systematic literature review

• Open access
• Published: 21 May 2024

Cite this article

You have full access to this open access article

• David Karl   ORCID: orcid.org/0000-0002-0326-5982 1  

331 Accesses

Explore all metrics

The substantial growth of e-commerce during the last years has led to a surge in consumer returns. Recently, research interest in consumer returns has grown steadily. The availability of vast customer data and advancements in machine learning opened up new avenues for returns forecasting. However, existing reviews predominantly took a broader perspective, focussing on reverse logistics and closed-loop supply chain management aspects. This paper addresses this gap by reviewing the state of research on returns forecasting in the realms of e-commerce. Methodologically, a systematic literature review was conducted, analyzing 25 relevant publications regarding methodology, required or employed data, significant predictors, and forecasting techniques, classifying them into several publication streams according to the papers’ main scope. Besides extending a taxonomy for machine learning in e-commerce, this review outlines avenues for future research. This comprehensive literature review contributes to several disciplines, from information systems to operations management and marketing research, and is the first to explore returns forecasting issues specifically from the e-commerce perspective.

Similar content being viewed by others

An E-Commerce Prototype for Predicting the Product Return Phenomenon Using Optimization and Regression Techniques

Forecasting Misused E-Commerce Consumer Returns

Extreme Learning Machine for Business Sales Forecasts: A Systematic Review

Avoid common mistakes on your manuscript.

1 Introduction

E-commerce has witnessed substantial growth rates in recent years and continues growing by double-digit margins (National Retail Federation/Appriss Retail 2023 ). However, lenient consumer return policies have resulted in $212 Billion worth of merchandise being returned to online retailers in the U.S. in 2022, accounting for 16.5% of online sales (National Retail Federation/Appriss Retail 2023 ). While high rates of consumer returns mainly concern specific sectors and product categories, online fashion retailing is particularly affected (Diggins et al. 2016 ). Recent studies report average shipment-related return rates for fashion retailers in the 40–50% range (Difrancesco et al. 2018 ; Karl and Asdecker 2021 ). In addition to missed sales and reduced profits (Zhao et al. 2020 ), consumer returns pose operational challenges (Stock and Mulki 2009 ), including unavoidable processing costs (Asdecker 2015 ) and uncertainties regarding logistics capacities, inventory management, procurement decisions, and marketing activities. Hence, effectively managing consumer returns is an essential part of the e-commerce business model (Urbanke et al. 2015 ).

Similar to the research conducted by Abdulla et al. ( 2019 ), this work focuses on consumer returns in online retailing (e-commerce), excluding the larger body of closed-loop supply chain (CLSC) management, which encompasses product returns related to end-of-life and end-of-use scenarios involving raw material recycling or remanufacturing. In contrast to CLSC returns, retail consumer returns are typically sent or given back unused or undamaged shortly after purchase, without any quality-related defects. These returns should be reimbursed to the consumer and are intended to be resold “as new” (de Brito et al. 2005 ; Melacini et al. 2018 ; Shang et al. 2020 ).

Regarding forecasting aspects, demand forecasting is a crucial activity for successful retail management (Ge et al. 2019 ). In contrast to demand and sales, returns constitute the “supply” side of the return process (Frei et al. 2022 ). Consequently, forecasting becomes a complex task and a significant challenge in managing returns due to the inherently uncertain nature of customer decisions regarding product retention (Frei et al. 2022 ). Moreover, return forecasts are interconnected with sales forecasts and promotional activities (Govindan and Bouzon 2018 ; Tibben-Lembke and Rogers 2002 ). Hence, forecasting objectives may vary, encompassing return quantities, timing (Hachimi et al. 2018 ), and even individual return probabilities. Minimizing return forecast errors is critical to reduce and minimize reactive planning (Hess and Mayhew 1997 ). Accurate forecasts rely on (1) comprehensive data collection, e.g., regarding consumer behavior, and (2) information and communications technology (ICT) for data processing, such as big data analytics. Despite extensive research in supply chain management (SCM), Barbosa et al. ( 2018 ) noted a lack of relevant publications exploring the "returns management" process of SCM in conjunction with big data analytics. Specifically, “the topic of forecasting consumer returns has received little attention in the academic literature” (Shang et al. 2020 ). Nonetheless, precise return forecasts positively impact reverse logistics activities’ economic, environmental, and social performance, primarily concerning quantity, quality, and timing predictions (Agrawal and Singh 2020 ). Hence, forecasting returns holds significant relevance across various supply chain stages.

1.1 Previous meta-research

Hess and Mayhew ( 1997 ) emphasized the need for extensive data analysis concerning reverse flows, which forms the basis for returns forecasting. Subsequently, research on consumer returns and reverse logistics has proliferated. Thus, before collecting data and reviewing the topic of consumer returns forecasting, we first examined existing reviews and meta-studies relevant to the subject matter. To accomplish this, we referred to Web of Science, Business Source Ultimate via EBSCOhost, JSTOR and the AIS Electronic Library as primary sources of knowledge (search term: "literature review" AND "return*" AND "forecast*”). As a secondary source, we appended the results of Google Scholar, Footnote 1 for which a different search term was used (intitle:"literature review" ("product return" OR "consumer return" OR "retail return" OR "e-commerce return") forecast) due to unavailable truncations and to reduce the vast amount of literature with financial focus the search term “return” would lead to. Table 1 presents the most pertinent literature reviews related to the scope of this paper.

Agrawal et al. ( 2015 ) identified research gaps within the realm of reverse logistics, finding “forecasting product returns” as a crucial future research path. However, among 21 papers focusing on “forecasting models for product returns”, the emphasis was predominantly on CLSC, reuse, remanufacturing, and recycling, which do not align with the aim of this review. Agrawal et al. also noted a lack of comprehensive analysis of underlying factors in returns forecasting, such as demographics or consumer behavior.

Similarly, Hachimi et al. ( 2018 ) addressed forecasting challenges within the broader context of reverse logistics. They classified their literature using various forecasting approaches: time series and machine learning, operations research methods, and simulation programs. The research gaps they identified included a limited number of influencing factors taken into account, the absence of established performance indicators, and methodological issues related to dynamic lot-sizing with returns. Although this review focused on reverse logistics, the call for research into predictors of future returns is equally applicable to consumer returns in e-commerce.

The review of Abdulla et al. ( 2019 ) centers on consumer returns within the retail context, particularly in relation to return policies. While they discuss consumer behavior and planning and execution of returns, they do not present any sources explicitly focused on forecasting issues.

Micol Policarpo et al. ( 2021 ) reviewed the literature on the use of machine learning (ML) in e-commerce, encompassing common goals of e-commerce studies (e.g., purchase prediction, repurchase prediction, and product return prediction) and the ML techniques suitable for supporting these goals. Their primary contribution is a novel taxonomy of machine learning in e-commerce, covering most of the identified goals. However, within the taxonomy developed, the aspect of return predictions is disregarded.

The most exhaustive literature review to date regarding product returns, conducted by Ambilkar et al. ( 2021 ), analyzed 518 papers and adopted a holistic reverse logistics approach encompassing all supply chain stages. The authors categorized the papers into six categories, including “forecasting product returns”, for which they found and concisely described 13 papers. Due to the broader research scope, none of the analyzed papers focused on consumer returns within the retail context.

The review by Duong et al. ( 2022 ) employed a hybrid approach combining machine learning and bibliometric analysis. Regarding forecasts of product returns, they identified three relevant papers (Clottey and Benton 2014 ; Cui et al. 2020 ; Shang et al. 2020 ) within the “operations management” category. They explicitly call for further research on predicting customer returns behavior in the pre-purchase stage, highlighting the importance of a better understanding of online product reviews and customers’ online interactions.

1.2 Research gaps and research questions

Why is a systematic literature review necessary for investigating consumer returns and forecasting? On the one hand, there are empirical and conceptual papers that touch upon this topic, including brief literature reviews that align with the subject’s focus (e.g., Hofmann et al. 2020 ). However, narrative reviews lack transparency and replicability (Tranfield et al. 2003 ) and often induce selection bias (Srivastava and Srivastava 2006 ) as they tend to approach a field from a specific perspective. In contrast, systematic reviews strive to present a holistic, differentiated, and more detailed picture, incorporating the complete available literature (Uman 2011 ). On the other hand, existing systematic reviews provide structured yet relatively superficial overviews of literature on end-of-use and end-of-life forecasting (Shang et al. 2020 ), but they do not specifically address consumer returns. Furthermore, we contend that a review dedicated to general reverse logistics forecasting would not adequately capture the distinctive context and requirements inherent in the consumer-retailer relationship within the realm of e-commerce (Abdulla et al. 2019 ).

Consequently, based on existing reviews and papers, we have identified research gaps worth examining more in detail: (1) Returns forecasting techniques and relevant predictors for the respective underlying purposes, especially in the context of e-commerce (RQ1 and RQ2); (2) the integration of return forecasts into an existing but incomplete taxonomy of machine learning in e-commerce (Micol Policarpo et al. 2021 ; RQ3); and (3) future research directions pertaining to e-commerce returns forecasting (RQ4). Therefore, this review aims to shed more light on consumer returns forecasting in the retail context. The following research questions outline the primary objectives:

RQ1: What key research problems (e.g., forecasting purposes, technological approaches) have been addressed in the literature on forecasting consumer returns over time?

RQ2: What are the …

Publication outlets and research disciplines,

Research types and methodologies,

Product categories and industries,

Data sources and characteristics,

Relevant forecasting predictors,

Techniques and algorithms

… used to address these key problems?

RQ3: How can returns forecasting be integrated into a taxonomy of machine learning in e-commerce?

RQ4: What are promising or emerging future research directions regarding forecasting consumer returns?

The paper is organized as follows: Sect.  2 describes selected fundamental concepts and the delimitation of the research field on consumer returns forecasting. Section  3 contains the methodology for the review, drawing on the PRISMA guideline (Page et al. 2021 ) while integrating the approaches of Denyer and Tranfield ( 2009 ) and Webster and Watson ( 2002 ). Section  4 presents the review’s main results, answering RQs 1 (Sect.  4.1 ), RQ2 (Sects.  4.2 – 4.5 ), and RQ 3 (Sect.  4.6 ). A research framework developed in Sect.  5 structures the discussion regarding future research directions (RQ4). Section  6 subsumes the overall contribution of this review.

2 Consumer returns and forecasting

2.1 consumer returns and return reasons.

Reverse product flows, commonly referred to as product returns, can be classified into three categories: manufacturing returns, distribution returns, and consumer returns (Shaharudin et al. 2015 ; Tibben-Lembke and Rogers 2002 ). Among these, consumer returns are further differentiated between returns in brick-and-mortar retail or mail-order/e-commerce returns (Tibben-Lembke and Rogers 2002 ) and are also known as commercial returns (de Brito et al. 2005 ) or retail (product) returns (Bernon et al. 2016 ). With sky-rocketing e-commerce sales, online consumer returns have emerged as the dominant segment, making them a highly relevant field of research (Abdulla et al. 2019 ; Frei et al. 2020 ). Additionally, the digitization of retail provides numerous opportunities for data collection, as digital customer accounts facilitate more efficient analytical monitoring of customer behavior (Akter and Wamba 2016 ). Simultaneously, as competitive pressures intensify in e-commerce due to increased price transparency and substitution possibilites, retailers aiming to stimulate impulse purchases face hightened return rates (Cook and Yurchisin 2017 ; Karl et al. 2022 ).

The spatial decoupling of supply and demand introduces a higher level of uncertainty for e-commerce customers regarding various product attributes compared to bricks-and-mortar retailing (Hong and Pavlou 2014 ). As consumers are unable to physically assess the products they order, this translates into returns being essential part of the e-commerce business model. Besides fit uncertainty, other reasons for returns exist. Stöcker et al. ( 2021 ) classify the drivers triggering consumer returns into consumer behavior related reasons (e.g., impulsive purchases, showrooming), fulfillment/service related reasons (e.g., wrong/delayed delivery) and information gap related reasons (product fit, insufficient visualization). By mitigating customers’ return reasons, retailers try to reduce the return likelihood (“return avoidance”) (Rogers et al. 2002 ). Another, but less promising way of reducing returns, is preventing customers who intend to return from actually doing so (e.g., by incurring additional effort or by rejecting returns) (Rogers et al. 2002 ).

Adapted from Abdulla et al. ( 2019 ) and Vakulenko et al. ( 2019 ), a simplified parallel process of a return transaction from the consumer’s and retailer’s perspective is visualized in Fig.  1 . Retailers can use forecasting in all transaction phases (Hess and Mayhew 1997 ). Targeting customer interventions pre-purchase (real-time forecasting) could be implemented by using dynamically generated (Dalecke and Karlsen 2020 ) digital nudging elements (Kaiser 2018 ; Thaler and Sunstein 2009 ; Zahn et al. 2022 ) in case of a predicted high return propensity. In the post-purchase phase, forecasting could stimulate different interventions (e.g., customer support) or can be helpful for logistics and inventory planning activities (Hess and Mayhew 1997 ). In the phase after the return decision, data analysis, including segmentation on different levels, e.g., for customers, products, or brands (Shang et al. 2020 ), can support managerial decision-making regarding assortment or (individualized) return policies for future orders (Abdulla et al. 2019 ). In other words, forecasting (or modeling) of returns in later phases of the process can substantiate interventions in earlier phases of the process (e.g., a temporary return policy change, or the suspension of product promotions due to particular forecasts). However, such data-driven interventions itself also represent an influencing factor to be taken into account in future forecasts; thus, different forecasting purposes can be linked, at least when it comes to the data required. All these interdependencies hint at the circularity of the returns process, with an adequate management of returns representing an opportunity for generating customer satisfaction and retention (Ahsan and Rahman 2016 ; Röllecke et al. 2018 ).

Purchase and return process concerning forecasting issues (adapted from Abdulla et al. 2019 ; Vakulenko et al. 2019 )

Although primarily focussing on the online retailers’ process, it is worth noting that the issue at hand is equally applicable to brick-and-mortar retail (Santoro et al. 2019 ), which can benefit from the application of advanced data analysis techniques for forecasting purposes (Hess and Mayhew 1997 ).

2.2 Forecasting purposes and corresponding techniques

Accurate forecasting holds significant importance in the realm of e-commerce. Precise demand forecasts (“predictions”) play a pivotal role in inventory planning, pricing, and promotions and ultimately impact the commercial success of retailers (Ren et al. 2020 ). Forecasting consumer returns affects similar business aspects and resorts to comparable existing technical procedures. The data science and statistics literature offers diverse methods and algorithms for forecasting consumer returns. The choice of approach depends on the specific objective, with the outcome variable being scaled accordingly. For instance, when forecasting whether a single product will be returned, the dependent variable is either binary or expressed as a propensity value ranging form 0 to 1. On the other hand, forecasting the quantitay or timing of returns entails continuous outcome variables. As a result, various techniques, from time-series forecasting to machine learning approaches can be applied, which will be briefly outlined in the subsequent sections.

2.2.1 Return classifications and propensities

A naïve method for determining the propensity or return decision forecast is using lagged (historical) return information (return rates), either for a given product, a given customer, or any other reference, to calculate a historical return probability (Hess and Mayhew 1997 ). Return rate forecasts are a reference-specific variant of forecasting return propensities.

Simple causal models based on statistical regression methods utilize one or more independent exogenous variables. The logistic regression (logit model) is employed when the dependent variable is binary or contains more nominal outcomes (multinomial logistic regression). For each observation, the binary logistic regression assesses the probability that the dependent variable takes the value “1” (Hastie et al. 2017 ). Consequently, this approach finds application for return decisions and return propensities. Comparatively, linear discriminant analysis (Fisher 1936 ) bears a resemblance to logistic regression by generating a linear combination of independent variables to best classify available data. This classification process involves determining a score for each observation, subsequently compared to a critical discriminant score threshold, and distinguishing between return and keep.

More sophisticated machine learning (ML) techniques such as neural networks, decision tree-based methods, ensemble learning, and boosting methods are highly suitable for this forecasting purpose. For a general exposition of ML techniques in the domain of e-commerce, we refer to Micol Policarpo et al. ( 2021 ). Additionally, for a comparative study of several state-of-the-art ML classification techniques, see Fernández-Delgado et al. ( 2014 ). Artificial Neural Networks (NN) consist of interconnected nodes (“neurons”) organized in layers, exchanging signals to ascertain a function that accurately assigns input data to corresponding outputs. Typically, supervised learning techniques such as backpropagation compare the network outputs with known actual values (Hastie et al. 2017 ). Notably, neural networks are the most popular machine learning algorithm in last years’ e-commerce research (Micol Policarpo et al. 2021 ), and deep learning extensions like Long Short-Term Memory (Bandara et al. 2019 ) are gaining attention. Decision Trees (DT) manifest as hierarchical structures of branches representing conjunctions of specific characteristics and leaf nodes denoting class labels. This approach endeavors to construct an optimal decision tree for classifying available observations. Many decision tree algorithms have been introduced to serve this purpose (e.g., Breiman et al. 1984 ; Pandya and Pandya 2015 ). Ensemble learning methods adopt a voting mechanism involving multiple algorithms to enhance predictive performance (Polikar 2006 ). Analogously, boosting and bagging techniques are incorporated in algorithms like AdaBoost or the tree-based Random Forest (RF) to augment the input data, aiming at more generalizable forecasting models less prone to overfitting issues (Hastie et al. 2017 ). Support Vector Machines (SVM) stand as another example of a supervised ML algorithm, having demonstrated efficacy in tackling classification problems within e-commerce (Micol Policarpo et al. 2021 ).

2.2.2 Return timing and volume forecasts

For product returns, timing is crucial in forecasting end-of-life, end-of-use, or remanufacturing returns that can occur years after the initial purchase (Petropoulos et al. 2022 ). In contrast, for consumer returns, the possible time window in which products are regularly returned in new condition with the aim of a refund is much shorter (usually less than 100 days and mostly less than 30 days), and priorities are more on forecasting return volumes. Forecasting return volumes can be multi-faceted, ranging from forecasting the total return volume a retailer has to process within its logistics department through forecasting product-specific return numbers up to forecasting costly return shares, e.g., return fraud volume. Because returns depend on fluctuating sales, time-series forecasting of return volumes performs only well with constant sales volumes or under risk-pooling (Petropoulos et al. 2022 ). Thus, for a naïve return volume forecast, sales forecasts for a given timeframe are multiplied by the lagged return rate (historical data of products/consumers or any other reference). Possible algorithms for estimating historical return rates include time series forecasting to causal predictions comprising ML approaches (Hachimi et al. 2018 ).

Time-series techniques, e.g., single exponential smoothing (SES) or Holt-Winters-approaches (HW), are based on the assumption that the future development of an outcome variable (e.g., return volume) is dependent on its past numbers, while time acts as the only predictor. Most of these models can be generalized as autoregressive moving averages (ARIMA) models, for which numerous extensions are available. These models can approximate more complex temporal relationships. Similarly, time-series regression models use univariate linear regression with time as a single exogenous variable.

The mentioned multivariate regression models are essential statistical tools and can predict metric variables such as return volume or time. The logic is to fit a linear function of a given set of input variables (“features”) to the outcome variable with the criteria of minimizing the residual sum of squares (Hastie et al. 2017 ). Many variants of regression models are derived from this logic (e.g., generalized linear models), and various extensions are built upon this base (e.g., LASSO for variable selection, Tibshirani 1996 ).

Emerging from more complex statistical methods and using the possibilities of continuously increasing computing power, IT-based machine learning (ML) approaches were developed. Some of these approaches have already been presented in Sect. 2.2.1, being suitable for predicting metric variables in addition to classification tasks, e.g., neural networks, decision tree algorithms, and especially ensemble techniques like random forests.

3 Methodology

Methodologically, the research process of this review follows the PRISMA guideline (Page et al. 2021 ) where applicable and is structured in five steps (Denyer and Tranfield 2009 ; Webster and Watson 2002 ): (1) question formulation; (2) locating studies; (3) study selection and evaluation; (4) (concept-centric) analysis and synthesis; and (5) reporting and using the results for defining an agenda for future research.

The first step refers to the research questions already formulated in the introduction. The second step involves selecting the databases and defining the search terms. In that respect, five scientific databases were selected, aiming at journal as well as conference publications: AIS Electronic Library (AISeL), Business Source Ultimate (BS) via EbscoHost, JSTOR (JS), Science Direct (SD), and Web of Science (WoS). To ensure inclusivity and to account for potential variations in spelling or phrasing, the final search strings incorporate truncations where applicable. The search query utilized in this review comprises two key components. Firstly, it pertains to consumer returns, encompassing products returned by consumers, primarily in the context of e-commerce, to the retailer. While it is recommended to use reasonably general search terms, the term “return” alone would yield results for various stages of reverse logistics and a vast amount of financial literature. Therefore, we conducted a more specific search using the phrase “consumer return*” and the related terms “e-commerce return*”, “product return*”, “return* product”, “customer return*”, and “retail return*”. Secondly, this paper specifically focuses on forecasting (“forecast*”), which can be alternately referred to as “predict*” or “prognos*”. The combination of these terms was searched for in the Title, Abstract and Keywords fields.

The search includes results up to the middle of 2022 and resulted in 725 initial search hits (see Fig.  2 ). As this review aims to identify papers dealing with consumer returns and forecasting, the inclusion criteria for eligibility were:

The title or keywords referred to consumer returns or forecasting (in a broader sense, including data preparation). A connection to the respective subject area and applicability to the retail domain should at least be plausible.

Manuscript in English: No important study would be written and published in a language different than English.

The paper has undergone a single- or double-blind peer-review process, either as a journal publication or as a publication in peer-reviewed conference proceedings.

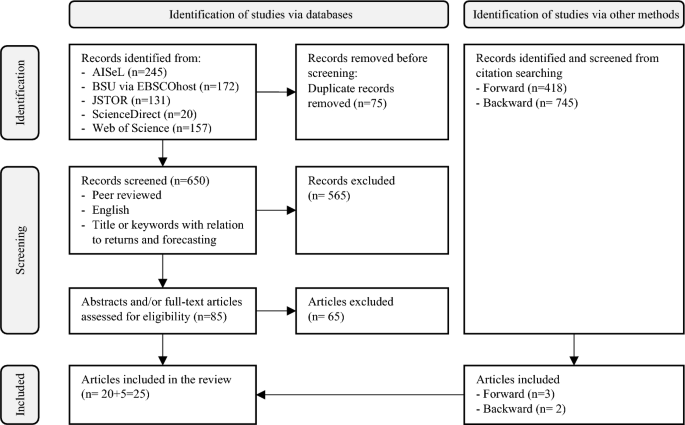
Research process flow diagram

In the third step, duplicates were removed, resulting in a set of 650 unique records. Subsequently, the papers underwent screening based on title, keywords, and language to determine whether they warranted further examination. This preliminary screening phase reduced the number of papers to 85. These papers’ abstracts and full texts were thoroughly reviewed to assess their relevance. This step encompasses all papers pertaining to returns forecasting for retailers or direct-selling manufacturers while excluding those focused on closed-loop supply chain management or remanufacturing, recycling, and end-of-life returns. Ultimately, a final sample of 20 publications was identified, serving as a foundation for identifying additional relevant papers (vom Brocke et al. 2009 ; Webster and Watson 2002 ) through a forward search using Google Scholar and snowballing via backward search. This process yielded an additional five papers, resulting in a total of 25 papers included for review (Table  2 ).

The fourth step comprises the analysis and synthesis of the relevant papers. Data, including bibliographic statistics, were collected in accordance with the research questions. A two-way concept-centric analysis, as described by Webster and Watson ( 2002 ), was conducted, encompassing confirmatory aspects based on the fundamentals outlined in Sect.  2 of this paper, as well as exploratory elements aimed at enriching existing categories and concepts. The objective was to comprehensively describe the relevant concepts, approaches, and dimensions discussed in the literature.

Moving on to the fifth and final step (Denyer and Tranfield 2009 ), the results are presented. Initially, the main scope of the papers included in the analysis is presented. Next, bibliographic data pertaining to the included papers are provided to offer a concise overview of the research area and its recent developments, followed by a content analysis and synthesis of the relevant literature to delve into the current state of research and highlight key findings. Finally, Sect.  5 outlines a research agenda for the domain (vom Brocke et al. 2009 ).

4 Results of the systematic review

After outlining the main scope of the relevant publications (4.1), a short bibliographic characterization (4.2) is given. Next, this section presents the results of the systematic review, focussing on the methodology and datasets used (4.3), predictors used for returns forecasting (4.4), and forecasting techniques employed (4.5). The integration of consumer returns forecasting into an existing taxonomy for e-commerce and machine learning (Micol Policarpo et al. 2021 ) summarizes and concludes the presentation of the results.

4.1 Overview and main scope of the relevant publications

Table 3 provides an overview of the forecasting purpose of the papers, the data source for the forecasting, the algorithms employed, and the predictors used in the forecasting models. The contributions of the respective papers regarding forecasting issues are summarized in the Appendix.

For identifying research streams, the publications are analyzed regarding the intention and main scope, as described in the abstract, the respective research questions, and the remainder of the papers. Most papers were assigned to an unequivocal research scope, while some contributed to two key topics (Fig.  3 ).

Classification of main scopes (n = 25; not mutually exclusive)

At first, we identified a stream of literature regarding the comparison of different forecasting models and algorithms (Asdecker and Karl 2018 ; Cui et al. 2020 ; Drechsler and Lasch 2015 ; Heilig et al. 2016 ; Hess and Mayhew 1997 ; Hofmann et al. 2020 ; Imran and Amin 2020 ). These papers use existing approaches, adapt them for individual forecasting purposes, apply models to one or more datasets, and compare and evaluate the resulting forecasting performance. One paper claims that the difference in forecasting accuracy of easily interpretable algorithms is relatively small compared to more sophisticated ML algorithms (Asdecker and Karl 2018 ). This statement is partially confirmed (Cui et al. 2020 ), as the ML algorithms show advantages over simpler models in the training data set but have lower prediction quality due to overfitting issues in the test data. Nevertheless, fine-tuned ML approaches (e.g., deep learning with TabNet) outperform simpler models and gain accuracy when correcting class imbalances during the data preparation phase (Imran and Amin 2020 ). When confronted with large class imbalances (e.g., low return rates), boosting algorithms like Gradient Boosting work well without oversampling (Hofmann et al. 2020 ). Fundamentally, ensemble models incorporating different techniques show the maximum possible accuracy (Asdecker and Karl 2018 ; Heilig et al. 2016 ). Forecasting of return timing is more erroneous than return decisions, and split-hazard-models outperform simple OLS approaches (Hess and Mayhew 1997 ). Time series prediction only works reliably when return rates do not fluctuate heavily (Drechsler and Lasch 2015 ).

The second stream we identified focuses on feature generation or selection and dataset preparation (Ahmed et al. 2016 ; Ding et al. 2016 ; Hofmann et al. 2020 ; Rezaei et al. 2021 ; Samorani et al. 2016 ; Urbanke et al. 2015 , 2017 ). Besides this central topic, some papers also compare different forecasting algorithms (Ahmed et al. 2016 ; Hofmann et al. 2020 ; Rezaei et al. 2021 ; Urbanke et al. 2015 , 2017 ). For example, random oversampling of data with large class imbalances can improve the performance of different forecasting algorithms, while models based only on sales/return history perform worse than models with more features (Hofmann et al. 2020 ). Two similar approaches are based on product, basket, and clickstream data, using different algorithms for feature extraction (Urbanke et al. 2015 , 2017 ). The first developed a Mahalanobis Feature Extraction algorithm, proving superior to other algorithms like principal component analysis or non-negative matrix factorization (Urbanke et al. 2015 ). The second develops a NeuralNet algorithm to extract interpretable features from a high-dimensional dataset, showing superior performance and giving reasonable interpretability of the most important factors (Urbanke et al. 2017 ). For the automated integration of different data sources into single flat tables and the generation of discriminating features, a rolling-path algorithm is developed, improving performance when data is imbalanced (Ahmed et al. 2016 ). Similarly, the software “Dataconda” can automatically generate and integrate relational attributes from different sources into a flat table, which is often the required prerequisite for forecasting algorithms (Samorani et al. 2016 ). A different selection approach clusters the features into groups and applies selection algorithms to the groups, aiming to select a smaller set of attributes (Rezaei et al. 2021 ). As quite an offshoot, one paper predicts a seller’s overall daily return volume dependent on his current “reputation” measured by tweets (Ding et al. 2016 ), which needs sentiment analysis to be integrated into the forecast.

A quite heterogenous research stream belongs to the development of algorithms, heuristics, and models that go beyond a straightforward adaption of existing approaches (Fu et al. 2016 ; Joshi et al. 2018 ; Li et al. 2018 ; Potdar and Rogers 2012 ; Rajasekaran and Priyadarshini 2021 ; Shang et al. 2020 ; Sweidan et al. 2020 ; Zhu et al. 2018 ). Potdar and Rogers ( 2012 ) developed a methodology for forecasting product returns based on reason codes and consumer behavior data. Fu et al. ( 2016 ) developed a conditional probability-based statistical model for predicting return propensities while revealing return reasons and outperforming some baseline benchmark models. Li et al. ( 2018 ) describe their “HyperGo” approach as a ‘framework’ and develop an algorithm for forecasting return intention after basket composition. Zhu et al. ( 2018 ) describe a “LoGraph” random walk algorithm for predicting returned customer/product combinations within their framework. Although Joshi et al. ( 2018 ) label their approach as a “framework”, they describe a specific two-stage algorithm for forecasting return decisions based on network science and ML. Rajasekaran and Priyadarshini ( 2021 ) developed a hybrid metaheuristic-based regression approach to predict return propensities.

Seven papers deal with concepts, meta-models, or substantial frameworks for returns forecasting (Fu et al. 2016 ; Fuchs and Lutz 2021 ; Heilig et al. 2016 ; Hofmann et al. 2020 ; Li et al. 2018 ; Shang et al. 2020 ; Zhu et al. 2018 ). A generic framework for a scalable cloud-based platform, which enables a vertical and horizontal adjustment of resources, could enable the practical real-time use of computationally intensive ML algorithms for forecasting returns in an e-commerce platform (Heilig et al. 2016 ). Two papers (Fuchs and Lutz 2021 ; Hofmann et al. 2020 ) are based on design science research (DSR, Hevner et al. 2004 ) for developing artifacts like meta models and frameworks. The first also refers to CRISP-DM, the “Cross Industry Standard Process for Data Mining” (Wirth and Hipp 2000 ), and develops a shopping-basket-based general forecasting approach suitable across different industries without domain knowledge and attributes needed (Hofmann et al. 2020 ). In a similar approach, based on the basket composition and user interactions, a generic model for real-time return prediction and intervention is developed (Fuchs and Lutz 2021 ) and prepared for integration into an ERP system. Fu et al. ( 2016 ) present a generalized return propensity latent model framework by decomposing returns into different inconsistencies (unmet product expectations, shipping issues, and both factors combined) and enriching the derived propensities with product features and customer profiles. Li et al. ( 2018 ) developed a “HyperGo” framework for forecasting the return intention in real-time after basket composition, including a hypergraph representation of historical purchase and return information. Similarly, Zhu et al. ( 2018 ) developed a “HyGraph” representation of historical customer behavior and customer/product similarity, combined with a “LoGraph” random-walk-based algorithm for predicting customer/product combinations that will be returned. Shang et al. ( 2020 ) discuss two opposing forecasting concepts, demonstrating that their predict-aggregate framework is superior to common and more naïve aggregate-predict approaches.

The last stream covers the detection and forecasting of return fraud and abuse (Drechsler and Lasch 2015 ; John et al. 2020 ; Ketzenberg et al. 2020 ; Li et al. 2019 ). On the employees’ side, one paper tries to automatically predict fraudulent return behavior of agents (employees), e.g., regarding unjustified refunds, by a penalized logit model, enabling a lift in detection (John et al. 2020 ). On the customers’ side, misused returns as a cost-incurring problem are the forecasting purpose of different time series prediction models (Drechsler and Lasch 2015 ). Instead of focussing on fraudulent transactions, a trust-aware random walk model identifies consumer anomalies, enabling retailers to apply targeted measures to specific customer groups (selfish, honest, fraud, and irrelevant customers) (Li et al. 2019 ). Similarly, returning customers can be categorized into abusive, legitimate, and nonreturners (Ketzenberg et al. 2020 ). Based on the characterization of abusive return behavior, a neural network classifier recaptures almost 50% of lost profits due to return abuse (Ketzenberg et al. 2020 ).

One paper (Sweidan et al. 2020 ) could not be assigned to the other scopes. It applies a single algorithm (RF) to a given dataset, and it contributes to the idea that only forecasted return decisions with high confidence should be used for targeted interventions due to their overproportional reliability.

4.2 Bibliographic literature analysis

Forecasting consumer returns has gained more research attention since 2016 (Fig.  4 ). The majority of the sample are conference publications, a couple of years ahead of the rise in journal publications. Compared to the publications on returns forecasting in the broader context of reverse logistics, which emerged in 2006 (Agrawal et al. 2015 ), the research on consumer returns moved into the spotlight about ten years later. This development is linked to a massive increase in e-commerce sales pre- and in-pandemic (Alfonso et al. 2021 ).

Publication trend by publication outlet

Out of 9 journal publications in the final sample, only two are published in the same journal (Journal of Operations Management). Out of 16 conference papers, 6 are published at conferences of the Association for Information Systems. In total, 16 of the 25 papers found are published in Information Systems (IS) and related outlets. Others can be assigned to the Management Science / Operations Research discipline (3), Strategy & Management in a broader sense (4), Marketing (1), and Research Methods (1) (Fig.  5 ).

Distribution of publication disciplines

Regarding the researchers’ geographical perspective, one paper was jointly published by authors from the US and China, 10 of 25 papers were authored from North America, followed by authors from Germany (7), India (3), China (1), and one paper each from Bangladesh, Singapore, and Sweden.

The most cited paper (200 external citations Footnote 2 ) from Hess and Mayhew ( 1997 ) could be thought of as the root of this research field (Table  4 ). However, only 10 out of 24 papers reference this work. Although Urbanke et al. ( 2015 ) received only 15 citations in total, within the sample, it is the second most cited paper (8 citations) and could eventually be classified as a research strand and origin of returns forecasting in the IS domain. Concerning the remaining papers, no unique strands of literature are recognizable based on citation analysis.

4.3 Methodology and data characterization

Regarding methodology, most of the papers start with a short narrative literature review regarding their respective focus. Not a single paper was based on interviews, surveys, questionnaires, or field experiments. 3 out of 25 papers formulated and tested conventional hypotheses. All of the publications use quantitative data for analysis and forecasting in a “case study” style, including numerical experiments based on real or simulated data.

Table 5 lists further details about the data used in the publications. 4 out of 25 papers rely on simulated data, and 23 out of 25 integrate actual data gained from a retailer. Two papers use both data types. 5 papers use more than one dataset (Ahmed et al. 2016 ; Cui et al. 2020 ; Rezaei et al. 2021 ; Samorani et al. 2016 ; Shang et al. 2020 ). The most frequently studied industry is fashion/apparel (10 papers), followed by five consumer electronics datasets. Two publications are based on data from a Taobao cosmetics retailer, and two datasets originate from general and wide assortment retailers. Two datasets incorporate building material and hardware store articles, and the detailed products are not named for three publications. Based on the previous studies, it is evident that consumer returns forecasting is most relevant for e-commerce, as 19 of the 25 publications refer to e-tailers. Nevertheless, 7 publications refer to brick-and-mortar retailing. Direct selling/marketing is represented in 2 data sets.

4.4 Predictors for consumer returns

There is an individual stream of research into factors that influence or help avoid consumer returns (e.g., Asdecker et al. 2017 ; De et al. 2013 ; Walsh and Möhring 2017 ), which is not part of this review. Nevertheless, the forecasting literature gives insights into return drivers, as the input variables (features, predictors, exogenous variables) for forecasting models represent some of these factors. Table 6 presents the most used predictors and tries to map these to the return driver categorization from Sect.  2.2 (Stöcker et al. 2021 ).

Although only a part of the publications interprets the predictors, some insights can be extracted. For total return volume , sales volume is the most critical predictor (Cui et al. 2020 ; Shang et al. 2020 ). Historical return volume trends can include behavioral aspects (e.g., impulse purchases) in a given timeframe (Cui et al. 2020 ; Shang et al. 2020 ). The product type significantly impacts the volume of returns (Cui et al. 2020 ), confirmed by widely varying return rates between different industries/sectors. Adding transaction-, customer-, or product-level predictors led to a surprisingly small forecasting accuracy gain (4% reduction of RMSE, Shang et al. 2020 ). The latter input variables may be more critical in forecasting return decisions and propensities.

Regarding product attributes , product or order price is one of the most common predictors, while some papers also include price discounts. In most models, price is hypothesized to increase returns (e.g., Asdecker and Karl 2018 ; Hess and Mayhew 1997 ). Promotional (discounted) orders also seem to result in more returns (Imran and Amin 2020 ), which could be explained by the stimulation of impulse purchases. Footnote 3 Brand perception influences return decisions (positive brands, lower returns) (Samorani et al. 2016 ). The order and return history of products are also relevant for predicting future orders and returns (Hofmann et al. 2020 ). Fit importance as a product attribute does not significantly change return propensities (Hess and Mayhew 1997 ).

Concerning customer attributes , gender seems essential, as female customers return significantly more items than men (Asdecker and Karl 2018 ; Fu et al. 2016 ). Younger customers show a slightly lower propensity to return (Asdecker and Karl 2018 ), but age played a more prominent role in predicting return fraud among employees than in customers (John et al. 2020 observed more fraud among younger employees). Customers with low credit scores returned more (Fu et al. 2016 ). The return history of a customer is possibly the most important predictor of future return behavior (Samorani et al. 2016 ). Some papers argue that consumer attributes, including purchase and return history (e.g., number and value of orders), are more relevant predictors than product or transaction profiles, reflecting more or less stable consumer preferences (Li et al. 2019 ).

Basket interactions are significant (Urbanke et al. 2017 ) in returns prediction. E.g., the larger the basket, the higher the return propensity will be (Asdecker and Karl 2018 ). Selection orders (same product in different sizes or colors) increase the return propensity (Li et al. 2018 ). Logistics attributes like delivery times only show minor effects (Asdecker and Karl 2018 ). Regarding the payment method, prepaid products are sent back less frequently than those with post-delivery payment options (Imran and Amin 2020 ), confirming other research results (Asdecker et al. 2017 ).

One literature stream focuses on the automated generation of features , as different and large-scale data sources need to be integrated and prepared for forecasting algorithms. Thus, possible interrelationships are complex to find manually, and ML approaches might outperform human analysts (Rezaei et al. 2021 ). While some approaches generate a large number of features that are hard to make sense of (Ahmed et al. 2016 ), the approach of Urbanke et al. ( 2017 ) aims to maintain the interpretability of automatically generated input variables. Some unexpected but meaningful interrelations might be found by automatic feature generation, e.g., the price of the last returned orders (Samorani et al. 2016 ). Nevertheless, automatic feature generation might be computation-intensive; thus, a parallel integration of feature selection could be advantageous for large data sets (Rezaei et al. 2021 ).

A remarkable research path based on artificial intelligence is integrating qualitative information like product reviews as predictors, going beyond numerical feedback (Rajasekaran and Priyadarshini 2021 ) or tweets. These data can be processed and made accessible for forecasting with ML-based sentiment analysis techniques (Ding et al. 2016 ).

4.5 Forecasting techniques and algorithms

To describe the techniques and algorithms employed, we sorted the papers by forecasting purpose as described in Sect.  2 , then assigned them to different algorithms, either from time series forecasting, statistical techniques, or ML algorithms. Table 7 lists all papers for which an assignment was possible, and the respective techniques used. If a comparison was possible, the best-performing algorithm is marked in this table.

The approaches listed in Table  7 are overlap-free, but some papers use more than one version of an approach, i.e., more than one algorithm from a category. E.g., TabNet is a DeepLearning version of neural networks (NN), and different variants of GradientBoosting are compared in one paper (CatBoost/LightGBM, not differentiated in the table below) (Imran and Amin 2020 ).

The algorithm used most frequently (Fig.  6 ) is the Random Forest algorithm (RF, 10 papers), followed by Support Vector Machines (SVM, 8 papers), Neural Networks (NN, 6 papers), logistic regression (Logit, 6 papers), GradientBoosting (5 papers), Ordinary Least Squares regression (OLS, 4 papers), Adaptive Boosting (AdaBoost), Linear Discriminant Analysis (LDA), and CART (Classification and Regression Trees, 3 papers each).

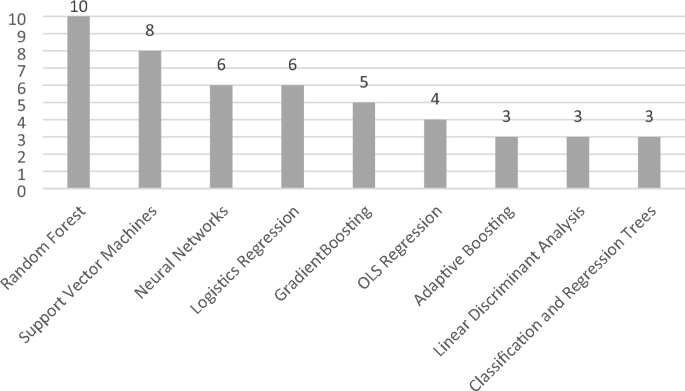
Most frequently used algorithms (used in at least three papers)

The papers focusing on return volume use time series forecasts like (AutoRegressive) Moving Averages (MA), Single Exponential Smoothing (SES), and Holt-Winters Smoothing (HWS) more frequently than ML algorithms. Nevertheless, when considering a predict-aggregate approach as proposed by Shang et al. ( 2020 ), these ML techniques could be helpful in forecasting return decisions first and cumulating the propensity results for the volume prediction in the second step.

In forecasting binary return decisions, Random Forests (RF) (Ahmed et al. 2016 ; Heilig et al. 2016 ; Ketzenberg et al. 2020 ), Neural Networks (NN) (Imran and Amin 2020 ; Ketzenberg et al. 2020 ), as well as Adaptive Boosting (AdaBoost) (Urbanke et al. 2015 , 2017 ) showed high prediction performance. The performance of different algorithms varies depending on the data set, the implementation, and the parameterization used. For this reason, it is hardly possible to make a generally valid statement regarding performance levels. Combining several algorithms in ensembles (Asdecker and Karl 2018 ; Heilig et al. 2016 ) seems advantageous, at least for retrospective analytical purposes, when the required computing resources are less relevant.

When evaluating different forecasting algorithms for return decisions, imbalanced classes (especially evident for low return shares in non-fashion datasets) seem to be handled differently depending on the algorithms. Class imbalances might distort comparison results in some publications. Random oversampling as a measure of data preparation can solve this problem (Hofmann et al. 2020 ).

High-performance algorithms are needed for real-time predictions, e.g., graph and random-walk-based (Li et al. 2018 ; Zhu et al. 2018 ). According to Li et al. ( 2018 ), the proposed algorithm “HyperGo” performs best for most performance metrics.

4.6 E-Commerce and machine learning taxonomy extension

In their literature review regarding the use of ML techniques in e-commerce, Micol Policarpo et al. ( 2021 ) propose a taxonomy to visualize specific ML algorithms in the context of e-commerce platforms. This novel kind of taxonomy is based on direct acyclic graphs, i.e., all input variables need to be fulfilled to reach the target. The first level of the taxonomy represents different target goals for the use of ML in e-commerce. While returns forecasting (“product return prediction”) is identified as an essential goal among others (purchase prediction, repurchase prediction, customer relationship management, discovering relationships between data, fraud detection, and recommendation systems), it was excluded from the taxonomy they developed, possibly because the review comprised only two relevant papers on this topic (Micol Policarpo et al. 2021 ). The review at hand proposes an extension of Micol Policarpo’s taxonomy, renaming the goal to “consumer returns forecasting”. This extension reflects and synthesizes the consumer returns forecasting studies reviewed.

The middle level of the taxonomy represents properties and features that support this superordinate goal. On this level, our extension does not include return fraud detection, which we propose to be integrated into the existing category of “fraud detection”, separated into transaction analysis and consumer analysis (Micol Policarpo et al. 2021 ). Circles represent the necessary data to execute the analysis, referring to categories introduced in (Micol Policarpo et al. 2021 ), with an additional “return history” category. The bottom level presents the algorithms described frequently, while some streamlining is required regarding the tools and approaches that seem the most common or most appropriate.

The schematic above (Fig.  7 ) is to be read as follows: In the context of E-Commerce  +  Artificial Intelligence (Layer 1), Consumer Return Forecasting (Layer 2) is an essential goal among six other goals. Layer 3 presents different purposes of analysis, which are the base for return forecasting. Realtime Basket Analysis is based on clickstream data and basket composition (browsing activities) to target interventions. Basket analysis benefits from customer and product information (dotted line). Graph-based approaches (Li et al. 2018 ; Zhu et al. 2018 ) are promising for real-time analysis due to their lower computing requirements, although cloud-based implementation of more complex algorithms or ensemble models might be feasible (Fuchs and Lutz 2021 ; Heilig et al. 2016 ; Hofmann et al. 2020 ). Customer Analysis and Product Analysis (e.g., Potdar and Rogers 2012 ) require adequate Data Preparation in the sense of input variable generation, extraction, and selection (Urbanke et al. 2015 , 2017 ). For these purposes, data regarding return history (e.g., Hofmann et al. 2020 ; Ketzenberg et al. 2020 ), purchase history (e.g., Cui et al. 2020 ; Fu et al. 2016 ), customer personal information (e.g., Heilig et al. 2016 ; Ketzenberg et al. 2020 ), clickstream data, and browsing activities are required as input (shown by cross-hatched circles). For each purpose, one or more possible algorithms are shown.

Proposed consumer returns forecasting extension to the E-commerce and Machine Learning techniques taxonomy of Micol Policarpo et al. ( 2021 , p. 13)

Compared to predicting purchase intention, return predictions seem to require more levels of data. Nevertheless, even simple rule-based interventions can promise benefits, e.g., selection orders that inevitably lead to a return shipment can be easily recognized (Hofmann et al. 2020 ; Sweidan et al. 2020 ). Different ML techniques are helpful for data preparation and input variable (feature) extraction and generation when considering more complex interrelations. NeuralNet is one example of an automatic selection of relevant features (Urbanke et al. 2017 ). These approaches are not only able to enhance forecasting accuracy (Rezaei et al. 2021 ) but can also render the many possible variables interpretable about their content.

5 Discussion

The analysis of the papers above revealed that research in this discipline seems heterogeneous and partly fragmented, and clear-cut research strands are still hard to identify. Thus, the existing literature calls for further publications to render this research field more comprehensive. Below, research opportunities are derived and embedded in a conceptual research framework derived from the results of the existing literature, also integrating the extension of the E-Commerce and Machine Learning taxonomy (Fig.  7 ). A conceptual framework improves the understanding of a complex topic by naming and explaining key concepts and their relationships important to a specific field (Jabareen 2009 ; Miles et al. 2020 ). Thus, this framework aims to organize problems and solutions discussed in the consumer returns forecasting literature and to embed and classify potential future research topics in the existing knowledge base (Ravitch and Riggan 2017 ). The subsections following the framework outline some potential research avenues (P1–P6) that have been touched on in the past but still leave considerable opportunities for further insights. These proposals should not be seen as comprehensive due to numerous other research opportunities in this field but rather as prioritization based on the current literature.

The framework derived (Fig.  8 ) underlines the interdisciplinary nature of this research field, integrating different perspectives (information systems research, marketing and operations perspective, and strategy and management perspective). From a managerial point of view, the literature included in this review is biased towards the information systems perspective. Thus, in contrast to the framework developed by Cirqueira et al. ( 2020 ) for purchase prediction, we do not take a process perspective but instead emphasize the interdependencies and interactions between research topics and highlight the managerial need to take a strategical perspective similar to the framework developed by Winklhofer et al. ( 1996 ). Consequently, a meta-layer on forecasting frameworks and practices includes the mainly technical development frameworks in this review but also accentuates the need for further research regarding actual organizational forecasting practices (e.g., P2, P5, P6). Around this meta-layer, some related research strands are linked in order to embed the topic of returns forecasting in the research landscape. E.g., in general, forecasting purchases and returns could be linked (P6), also effecting inventory decisions.

Conceptual Consumer Return Forecasting Framework

The center of the framework consists of three dimensions, namely purposes and tasks, predictors, and techniques. Depending on the strategical purpose, tasks are derived that determine (1) the data (predictors) needed and (2) the usable techniques to execute the forecasting. Different forecasting techniques require an individual set of predictors, whereas the availability of specific data allows and determines the use of more or less sophisticated algorithms.

In the literature, some forecasting purposes were more pronounced (return decisions or propensities), while others have gained less attention (return timing, P1). Regarding the data necessary for accurate forecasting, the return predictors discussed often were hardly comparable, as they originated from different data sources, different industries, were related to different dimensions, or were aggregated in another way. Systematically linking forecasting predictors and research on return drivers and reasons could contribute significant insights (P4) that, from a marketing perspective, may support the development of effective preventive instruments. Furthermore, the literature mainly refers to the fashion or consumer electronics industry, leaving room to validate the findings in the context of other industries (P3).

When (automatically) selecting or creating predictors, the boundaries between predictors and prediction techniques are blurred as machine learning algorithms prepare the input data before executing a forecasting model. Regarding forecasting techniques, time series forecasting was seldom used in recent publications. Machine learning algorithms were the most popular subject of investigation, with random forests, support vector machines, and neural networks as the most popular implementations. Classical statistical models like logit models for return decisions or OLS regression gained less research attention. Literature on end-of-life return forecasting could complement the research on techniques and their accuracy. Most publications used technical indicators for assessing the accuracy of forecasting models, which is the information systems perspective. From a managerial position, evaluating (monetary) performance outcomes (e.g., Ketzenberg et al. 2020 ) of forecasting systems should be more relevant.

5.1 Research proposal P1: return timing for consumer returns

Toktay et al. ( 2004 ) encouraged the integrated forecasting of the return rate and the return time lag. In line with this, Shang et al. ( 2020 ) criticize the missing focus on the timing of return forecasts. The reviewed literature confirms that forecasting return propensities and decisions are more prominent than timing and volume forecasts. While the knowledge of when a return is expected is vital in managing end-of-life returns that occur over the years, for retail consumer returns, return periods are mostly 14–30 days. Thus, the variability of return timing seems limited compared to end-of-life returns in this context, which makes this forecasting purpose less critical. Nevertheless, some retailers offer up to 100 days of free returns (e.g., Zalando). Consequently, more studies about the importance of return timing forecasts in the e-commerce context from a business and planning perspective and their interdependence with return processing or warehousing issues could shed light on this topic and complement the current literature (Toktay et al. 2004 ; Shang et al. 2020 ).

5.2 Research proposal P2: realtime forecasting systems

Another research gap became apparent regarding the real-time use of forecasting systems and the associated activities and interventions, building on the initial research and the frameworks already published (e.g., Heilig et al. 2016 ; Urbanke et al. 2015 ). The generic framework developed by Fuchs and Lutz ( 2021 ) could serve as a launching pad for this stream of research.

The paper from Ketzenberg et al. ( 2020 ) could act as a stimulus and inspiration for a similar approach, not only focusing on return abuse as already examined but on return forecasting in general, the possible associated interventions for various consumer groups, and the resulting consequences for the retailer’s profit. Even the methodology of customer classification could be helpful for many retailers in targeting interventions.

Before real-time return forecasting is implemented, associated preventive return management instruments need to be designed and evaluated. Many of these measures are discussed (e.g., Urbanke et al. 2015 ; Walsh et al.  2014 ), but an overview of which preventive measures (for some examples, see Walsh and Möhring 2017 ) are effective in general (1) and how forecasting accuracy interdepends with their usefulness (2) is still missing, to substantially link the topics of forecasting and interventions. No answers could be found to the call by Urbanke et al. ( 2015 ) for field experiments to investigate such a link.

Thanks to cloud and parallelization technologies and the associated scalability of computing power (Bekkerman et al. 2011 ), algorithm runtimes are becoming less relevant. However, especially for real-time use, it should be evaluated which algorithms and underlying datasets exhibit an appropriate relationship between the targeted forecasting accuracy, the expected benefit, and the required computing power.

Recommendations concerning the algorithms and techniques can be derived (Urbanke et al. 2015 ), and a generic implementation framework was developed (Fuchs and Lutz 2021 ). However, from a business perspective, no contributions could be found regarding the actual implementation of real-time forecasting systems, the interventions involved, and their impact on consumer behavior or profit (also see proposal P5). In addition, the implementations of such systems need to be analyzed concerning the cost-effectiveness of the required investments.

5.3 Research proposal P3: cross-industry and multiple dataset studies

Many publications rely on a single data set from a specific industry or retailer. Only a few compare several retailers (e.g., Cui et al. 2020 ). Studies including and comparing different countries are missing, which is especially interesting since legal regulations for returns vary. For example, in contrast to the U.S., citizens within the EU are granted a 14-day right of withdrawal for distance selling purchases. Footnote 4 Although in most developed countries, liberal and broadly comparable returns policies are standard in practice due to competitive pressure, the generalizability of the results is frequently limited. One remedy for this problem is to use multiple data sets from different retailers (e.g., electronics vs. jewelry, Shang et al. 2020 ). Admittedly, it is challenging to simultaneously collaborate with several retailers and to combine different data sets, due to reasons of preserving corporate privacy and synchronizing various data sources. Nevertheless, research needs to draw conclusions from single data points, as well as logically replicate or falsify those results by integrating more data points to find patterns of similarities and differences, either within or cross-study (Hamermesh 2007 ). Therefore, we suggest that future studies acquire industry-related datasets from several retailers at once or replicate existing studies, which aligns with the aim and scope of Management Review Quarterly (Block and Kuckertz 2018 ). Cross-industry or cross-country manuscripts, which go beyond the mere assertion of an industry-agnostic approach (Hofmann et al. 2020 ) and jointly investigate data from several sectors, would promise an additional gain in knowledge and could be less challenging from a privacy perspective.

5.4 Research proposal P4: extended study of relevant predictors in forecasting applications

Although not the main focus of this review, predictors of consumer returns are especially interesting for marketing and e-commerce research, for example, regarding preventive measures for avoiding returns. In the past, many consumer return papers highlighted single aspects or a limited selection of return drivers or preventive measures employed but rarely attempted to model return behavior as comprehensively as possible. However, the latter is the very objective of returns forecasting, which is why the findings on influencing factors in articles with a forecasting focus tend to be more holistic, although not sufficiently complete (Hachimi et al. 2018 ). Some return reasons named in the literature (e.g., Stöcker et al. 2021 ) have not yet been included in forecasting approaches, and vice versa, only a part of the influencing factors investigated could be mapped to a return reason categorization. The reason categories assigned (Sect.  4.4 , Table  6 ) still contain some uncertainty. For example, a customer’s product return history may reflect the general returning behavior of a customer to some extent, while it can not be ruled out that repeated logistical problems caused the returns. Product attributes may reflect information gaps that consumers can only assess after physically inspecting the product, whereas product price–frequently cited and influential product attribute—is only related to information gaps when considering the price-performance ratio (Stöcker et al. 2021 ). Technical information about the web browser or device used by the customer is difficult to categorize, as it may reflect behavioral (impulse-driven mobile shopping) as well as informational (small display with few visible information) aspects. The payment method chosen by a customer, for example, could not be linked to one of the reason categories.

This reasoning should serve as a basis for linking forecasting predictors and return reasons more closely in the future. For example, the respective relative weighting of return drivers is more likely to be obtained considering as many factors involved as possible, minimizing the unexplained variation. From the reviewed literature, we extracted 18 different return predictor categories. For instance, seven papers (Cui et al. 2020 ; Fu et al. 2016 ; Ketzenberg et al. 2020 ; Li et al. 2018 , 2019 ; Urbanke et al. 2015 , 2017 ) integrated more than five predictor categories. But even though some papers integrate more than 5,000 features for automated feature selection (Ketzenberg et al. 2020 ), there are still combinations of input variable categories that have not been investigated and, more importantly, interpreted yet. Therefore, we call for more comprehensive research on return predictors and their interpretation, including associated preventive return measures, in the context of return forecasting.

5.5 Research proposal P5: descriptive case studies and business implementations surveys

This review identified a lack of publications regarding the actual benefit and the diffusion of consumer returns forecasting systems in different scopes and industries, building on the papers presenting return forecasting frameworks. In 2013, less than half of German retailers analyzed the likelihood of returns (Pur et al. 2013 ). Most of those who did were using naïve approaches that might be outperformed by the models presented in this review. Still, we do not know the status quo regarding the degree of adoption and implementation of forecasting systems for consumer returns in e-commerce firms (e.g., see Mentzer and Kahn 1995 for sales forecasting systems), country-specific and internationally.

Furthermore, the impact of return forecasting practices on company performance should be examined not only based on modeling, but on retrospective data (e.g., see Zotteri and Kalchschmidt 2007 for a similar study on demand forecasting practices in manufacturing). A possible hypothesis to examine might be that accuracy measures like RMSE or precision/recall and subsequently even the choice of the most accurate machine learning algorithm (e.g., see Asdecker and Karl 2018 ) are less relevant from a business perspective: (1) No algorithm clearly outperforms all other algorithms, and (2) the correlation between technical indicators and business value is unstable (Leitch and Tanner 1991 ). Methodologically, implementations of consumer returns forecasting in e-commerce should thus be surveyed and analyzed with multivariate statistical methods to examine critical factors and circumstances of return forecasting systems – similar to publications on reverse logistics performance (Agrawal and Singh 2020 ).

5.6 Research proposal P6: holistic forward and backward forecasting framework for e-tailers

Some publications present frameworks for forecasting returns (Fuchs and Lutz 2021 ). Nevertheless, in the past, forecasting in retail and especially e-commerce commonly focused more on demand (Micol Policarpo et al. 2021 ) than returns. Current approaches for demand forecasting try to predict individual purchase intentions based on click-stream data, online session attributes, and customer history (e.g., Esmeli et al. 2021 ). Our systematic approach could not identify any paper that connects and integrates both directions in e-commerce forecasting, neither conceptual (frameworks) nor with a quantitative or case-study-like approach. Nevertheless, first implementations of return predictions in inventory management are presented (e.g., Goedhart et al. 2023 ). Subsequently, similar to Goltsos et al. ( 2019 ), we call for research addressing both demand and return uncertainties by providing a holistic forecasting framework in the context of e-commerce.

6 Conclusion

To date, no systematic literature review has undertaken an in-depth exploration of the topic of forecasting consumer returns in the e-commerce context. Previous reviews have primarily focused on product returns forecasting within the broader context of reverse logistics or closed-loop supply chain management (Agrawal et al. 2015 ; Ambilkar et al. 2021 ; Hachimi et al. 2018 ). Regrettably, the interdisciplinary nature of this subject has often been overlooked, also neglecting the inclusion of results from information systems research.

The review first aims to provide an overview of the existing literature (Kraus et al. 2022 ) on forecasting consumer returns. The findings confirm that this once novel topic has significantly evolved in recent years. Consequently, this review is timely in examining current gaps and establishing a robust foundation for future research, which forms a second goal of systematic reviews (Kraus et al. 2022 ). The current body of work encompasses various aspects from different domains, including marketing, operations management/research, and information systems research, highlighting the interdisciplinary nature of e-commerce analytics and research. As a result, future studies can find suitable publication outlets in domain-specific as well as methodologically oriented journals and conferences.

Scientifically, the algorithms and predictors investigated in previous research serve as a foundational reference for subsequent publications and informed decisions regarding research design, ensuring that specific predictors and techniques are not overlooked. Researchers can utilize this review and the research framework developed as a structuring guide, e.g., regarding relevant publications on already examined algorithms or predictors.

Managerially, the extended taxonomy for machine learning in e-commerce (Micol Policarpo et al. 2021 ) can serve as a guideline for implementing forecasting systems for consumer returns. This review classifies possible prediction purposes, allowing businesses to apply them based on their respective challenges. Exploring the most frequently used predictors reveals the data that must be collected for the respective purposes. This review also offers valuable insights into data (pre-)processing and highlights popular algorithms. Furthermore, frameworks are outlined that support the design and implementation phase of such forecasting systems, supporting analytical purposes or enabling direct interventions during the online shopping process flow. As an exemplary and promising application, return policies could be personalized (Abbey et al. 2018 ) by identifying opportunistic or fraudulent basket compositions or high-returning customers, thereby reducing unwanted returns (Lantz and Hjort 2013 ).

Finally, a limitation of this review is the exclusion of forecasting algorithms for end-of-use returns, which could potentially be applicable to forecasting shorter-term retail consumer returns. However, the closed-loop supply chain and reverse logistics literature has been systematically excluded. Hence, future reviews could synthesize previous reviews on reverse logistics forecasting with the more detailed findings presented in this paper.

The use of Google Scholar for systematic scientific information search is controversely discussed (e.g., Halevi et al. 2017 ) due to the missing quality control and indexing guidelines, as well as limited advanced search options. But as an additional database for an initial search, the wide coverage of this search system can enrich the results.

External citations according to Google Scholar, which is preferable for citation tracking over controlled databases (Halevi et al. 2017 ).

Other literature also describes a counteracting effect of a reduced price due to lowered quality expectations or a higher perceived value of the “deal” itself (e.g., Sahoo et al. 2018 ).

It should be noted that the relevance of the forecasting topic depends on the maturity of the e-commerce sector. In most developing countries, B2C e-commerce is comparatively young and consumer returns are not yet a common phenomenon, which is why research on return forecasts is relatively insignificant for these countries.

References

Abbey JD, Ketzenberg ME, Metters R (2018) A more profitable approach to product returns. MIT Sloan Manag Rev 60(1):71–74

Google Scholar  

Abdulla H, Ketzenberg ME, Abbey JD (2019) Taking stock of consumer returns: a review and classification of the literature. J Oper Manag 65(6):560–605. https://doi.org/10.1002/joom.1047

Article   Google Scholar  

Agrawal S, Singh RK (2020) Forecasting product returns and reverse logistics performance: structural equation modelling. MEQ 31(5):1223–1237. https://doi.org/10.1108/MEQ-05-2019-0109

Agrawal S, Singh RK, Murtaza Q (2015) A literature review and perspectives in reverse logistics. Resour Conserv Recycl 97:76–92. https://doi.org/10.1016/j.resconrec.2015.02.009

Ahmed F, Samorani M, Bellinger C, Zaiane OR (2016) Advantage of integration in big data: feature generation in multi-relational databases for imbalanced learning. In: Proceedings of the 4th IEEE international conference on big data, pp 532–539. https://doi.org/10.1109/BigData.2016.7840644

Ahsan K, Rahman S (2016) An investigation into critical service determinants of customer to business (C2B) type product returns in retail firms. Int Jnl Phys Dist Log Manage 46(6/7):606–633. https://doi.org/10.1108/IJPDLM-09-2015-0235

Akter S, Wamba SF (2016) Big data analytics in e-commerce: a systematic review and agenda for future research. Electron Markets 26(2):173–194. https://doi.org/10.1007/s12525-016-0219-0

Alfonso V, Boar C, Frost J, Gambacorta L, Liu J (2021) E-commerce in the pandemic and beyond. BIS Bulletin 36

Ambilkar P, Dohale V, Gunasekaran A, Bilolikar V (2021) Product returns management: a comprehensive review and future research agenda. Int J Prod Res. https://doi.org/10.1080/00207543.2021.1933645

Asdecker B (2015) Returning mail-order goods: analyzing the relationship between the rate of returns and the associated costs. Logist Res 8(1):1–12. https://doi.org/10.1007/s12159-015-0124-5

Asdecker B, Karl D (2018) Big data analytics in returns management–are complex techniques necessary to forecast consumer returns properly? In: Proceedings of the 2nd international conference on advanced research methods and analytics, Valencia, pp 39–46. https://doi.org/10.4995/CARMA2018.2018.8303

Asdecker B, Karl D, Sucky E (2017) Examining drivers of consumer returns in e-tailing with real shop data. In: Proceedings of the 50th Hawaii international conference on system sciences (HICSS). https://doi.org/10.24251/HICSS.2017.507

Bandara K, Shi P, Bergmeir C, Hewamalage H, Tran Q, Seaman B (2019) Sales Demand forecast in e-commerce using a long short-term memory neural network methodology. In: Gedeon T, Wong KW, Lee M (eds) Neural information processing: proceedings of the 26th international conference on neural information processing, 1st edn., vol 11955, pp 462–474. https://doi.org/10.1007/978-3-030-36718-3_39

Barbosa MW, La Vicente AdC, Ladeira MB, de Oliveira MPV (2018) Managing supply chain resources with big data analytics: a systematic review. Int J Log Res Appl 21(3):177–200. https://doi.org/10.1080/13675567.2017.1369501

Bekkerman R, Bilenko M, Langford J (2011) Scaling up machine learning. In: Proceedings of the 17th ACM SIGKDD international conference tutorials, p 1. https://doi.org/10.1145/2107736.2107740

Bernon M, Cullen J, Gorst J (2016) Online retail returns management. Int J Phys Distrib Logist Manag 46(6/7):584–605. https://doi.org/10.1108/IJPDLM-01-2015-0010

Block J, Kuckertz A (2018) Seven principles of effective replication studies: strengthening the evidence base of management research. Manag Rev Q 68(4):355–359. https://doi.org/10.1007/s11301-018-0149-3

Breiman L, Friedman JH, Olshen RA, Stone CJ (1984) Classification and regression trees. Wadsworth & Brooks/Cole Advanced Books & Software, Monterey, CA

Cirqueira D, Hofer M, Nedbal D, Helfert M, Bezbradica M (2020) Customer purchase behavior prediction in e-commerce: a conceptual framework and research Agenda. In: Ceci M, Loglisci C, Manco G, Masciari E, Raś Z (eds) New frontiers in mining complex patterns, vol 11948. Springer, Cham, pp 119–136. https://doi.org/10.1007/978-3-030-48861-1_8

Chapter   Google Scholar  

Clottey T, Benton WC (2014) Determining core acquisition quantities when products have long return lags. IIE Trans 46(9):880–893. https://doi.org/10.1080/0740817X.2014.882531

Cook SC, Yurchisin J (2017) Fast fashion environments: consumer’s heaven or retailer’s nightmare? Int J Retail Distrib Manag 45(2):143–157. https://doi.org/10.1108/IJRDM-03-2016-0027

Cui H, Rajagopalan S, Ward AR (2020) Predicting product return volume using machine learning methods. Eur J Oper Res 281(3):612–627. https://doi.org/10.1016/j.ejor.2019.05.046

Dalecke S, Karlsen R (2020) Designing dynamic and personalized nudges. In: Chbeir R, Manolopoulos Y, Akerkar R, Mizera-Pietraszko J (eds) Proceedings of the 10th international conference on web intelligence, mining and semantics. ACM, New York, pp 139–148. https://doi.org/10.1145/3405962.3405975

De P, Hu Y, Rahman MS (2013) Product-oriented web technologies and product returns: an exploratory study. Inf Syst Res 24(4):998–1010. https://doi.org/10.1287/isre.2013.0487

de Brito MP, Dekker R, Flapper SDP (2005) Reverse logistics: a review of case studies. In: Klose A, Fleischmann B (eds) Distribution logistics, vol 544. Springer. Berlin, Heidelberg, pp 243–281

Denyer D, Tranfield D (2009) Producing a systematic review. In: Buchanan DA, Bryman A (eds) The Sage handbook of organizational research methods. Sage, Thousand Oaks, CA, pp 671–689

Difrancesco RM, Huchzermeier A, Schröder D (2018) Optimizing the return window for online fashion retailers with closed-loop refurbishment. Omega 78:205–221. https://doi.org/10.1016/j.omega.2017.07.001

Diggins MA, Chen C, Chen J (2016) A review: customer returns in fashion retailing. In: Choi T-M (ed) Analytical modeling research in fashion business. Springer, Singapore, pp 31–48. https://doi.org/10.1007/978-981-10-1014-9_3

Ding Y, Xu H, Tan BCY (2016) Predicting product return rate with “tweets”. In: Proceedings of the 20th Pacific asia conference on information systems

Drechsler S, Lasch R (2015) Forecasting misused e-commerce consumer returns. In: Logistics management: proceedings of the 9th conference “Logistikmanagement”. Cham, pp 203–215.

Duong QH, Zhou L, Meng M, van Nguyen T, Ieromonachou P, Nguyen DT (2022) Understanding product returns: a systematic literature review using machine learning and bibliometric analysis. Int J Prod Econ 243:108340. https://doi.org/10.1016/j.ijpe.2021.108340

Esmeli R, Bader-El-Den M, Abdullahi H (2021) Towards early purchase intention prediction in online session based retailing systems. Electron Markets 31(3):697–715. https://doi.org/10.1007/s12525-020-00448-x

Fernández-Delgado M, Cernadas E, Barro S, Amorim D (2014) Do we need hundreds of classifiers to solve real world classification problems? J Mach Learn Res 15(1):3133–3181

Fisher RA (1936) The use of multiple measurements in taxonomic problems. Ann Eugen 7(2):179–188. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x

Frei R, Jack L, Brown S (2020) Product returns: a growing problem for business, society and environment. IJOPM 40(10):1613–1621. https://doi.org/10.1108/IJOPM-02-2020-0083

Frei R, Jack L, Krzyzaniak S-A (2022) Mapping product returns processes in multichannel retailing: challenges and opportunities. Sustainability 14(3):1382. https://doi.org/10.3390/su14031382

Fu Y, Liu G, Papadimitriou S, Xiong H, Li X, Chen G (2016) Fused latent models for assessing product return propensity in online commerce. Decis Support Syst 91:77–88. https://doi.org/10.1016/j.dss.2016.08.002

Fuchs K, Lutz O (2021) A stitch in time saves nine–a meta-model for real-time prediction of product returns in ERP systems. In: Proceedings of the 29th european conference on information systems

Ge D, Pan Y, Shen Z-J, Di Wu, Yuan R, Zhang C (2019) Retail supply chain management: a review of theories and practices. J Data Manag 1:45–64. https://doi.org/10.1007/s42488-019-00004-z

Goedhart J, Haijema R, Akkerman R (2023) Modelling the influence of returns for an omni-channel retailer. Eur J Oper Res 306(3):1248–1263. https://doi.org/10.1016/j.ejor.2022.08.021

Goltsos TE, Ponte B, Wang SX, Liu Y, Naim MM, Syntetos AA (2019) The boomerang returns? Accounting for the impact of uncertainties on the dynamics of remanufacturing systems. Int J Prod Res 57(23):7361–7394. https://doi.org/10.1080/00207543.2018.1510191

Govindan K, Bouzon M (2018) From a literature review to a multi-perspective framework for reverse logistics barriers and drivers. J Clean Prod 187:318–337. https://doi.org/10.1016/j.jclepro.2018.03.040

Hachimi HEL, Oubrich M, Souissi O (2018) The optimization of reverse logistics activities: a literature review and future directions. In: Proceedings of the 5th IEEE international conference on technology management, operations and decisions, Piscataway, NJ, pp 18–24. https://doi.org/10.1109/ITMC.2018.8691285

Halevi G, Moed H, Bar-Ilan J (2017) Suitability of Google Scholar as a source of scientific information and as a source of data for scientific evaluation—review of the Literature. J Informet 11(3):823–834. https://doi.org/10.1016/j.joi.2017.06.005

Hamermesh DS (2007) Viewpoint: Replication in economics. Can J of Econ 40(3):715–733. https://doi.org/10.1111/j.1365-2966.2007.00428.x

Hastie T, Tibshirani R, Friedman JH (2017) The elements of statistical learning: data mining, inference, and prediction. Springer, New York, NY

Heilig L, Hofer J, Lessmann S, Voß S (2016) Data-driven product returns prediction: a cloud-based ensemble selection approach. In: Proceedings of the 24th european conference on information systems

Hess JD, Mayhew GE (1997) Modeling merchandise returns in direct marketing. J Direct Market 11(2):20–35. https://doi.org/10.1002/(SICI)1522-7138(199721)11:2<20:AID-DIR4>3.0.CO;2-#

Hevner A, March S, Park J, Ram S (2004) Design science in information systems research. MIS Q 28(1):75. https://doi.org/10.2307/25148625

Hofmann A, Gwinner F, Fuchs K, Winkelmann A (2020) An industry-agnostic approach for the prediction of return shipments. In: Proceedings of the 26th Americas conference on information systems, pp 1–10

Hong Y, Pavlou PA (2014) Product fit uncertainty in online markets: nature, effects, and antecedents. Inf Syst Res 25(2):328–344. https://doi.org/10.1287/isre.2014.0520

Imran AA, Amin MN (2020) Predicting the return of orders in the e-tail industry accompanying with model interpretation. Procedia Comput Sci 176:1170–1179. https://doi.org/10.1016/j.procs.2020.09.113

Jabareen Y (2009) Building a conceptual framework: philosophy, definitions, and procedure. Int J Qual Methods 8(4):49–62. https://doi.org/10.1177/160940690900800406

John S, Shah BJ, Kartha P (2020) Refund fraud analytics for an online retail purchases. J Bus Anal 3(1):56–66. https://doi.org/10.1080/2573234X.2020.1776164

Joshi T, Mukherjee A, Ippadi G (2018) One size does not fit all: predicting product returns in e-commerce platforms. In: Proceedings of the 10th IEEE/ACM international conference on advances in social networks analysis and mining, pp 926–927. https://doi.org/10.1109/ASONAM.2018.8508486

Kaiser D (2018) Individualized choices and digital nudging: multiple studies in digital retail channels. Karlsruher Institut für Technologie (KIT). https://doi.org/10.5445/IR/1000088341

Karl D, Asdecker B (2021) How does the Covid-19 pandemic affect consumer returns: an exploratory study. In: Proceedings of the 50th european marketing academy conference, vol 50

Karl D, Asdecker B, Feddersen-Arden C (2022) The impact of displaying quantity scarcity and relative discounts on sales and consumer returns in flash sale e-commerce. In: Proceedings of the 55th hawaii international conference on system sciences. https://doi.org/10.24251/HICSS.2022.556

Ketzenberg ME, Abbey JD, Heim GR, Kumar S (2020) Assessing customer return behaviors through data analytics. J Oper Manag 66(6):622–645. https://doi.org/10.1002/joom.1086

Kraus S, Breier M, Lim WM, Dabić M, Kumar S, Kanbach D, Mukherjee D, Corvello V, Piñeiro-Chousa J, Liguori E, Palacios-Marqués D, Schiavone F, Ferraris A, Fernandes C, Ferreira JJ (2022) Literature reviews as independent studies: guidelines for academic practice. Rev Manag Sci 16(8):2577–2595. https://doi.org/10.1007/s11846-022-00588-8

Lantz B, Hjort K (2013) Real e-customer behavioural responses to free delivery and free returns. Electron Commer Res 13(2):183–198. https://doi.org/10.1007/s10660-013-9125-0

Leitch G, Tanner JE (1991) Economic forecast evaluation: profits versus the conventional error measures. Am Econ Rev 81(3):580–590

Li X, Zhuang Y, Fu Y, He X (2019) A trust-aware random walk model for return propensity estimation and consumer anomaly scoring in online shopping. Sci China Inf Sci 62(5). https://doi.org/10.1007/s11432-018-9511-1

Li J, He J, Zhu Y (2018) E-tail product return prediction via hypergraph-based local graph cut. In: Proceedings of the 24th ACM sigkdd international conference on knowledge discovery & data mining, New York, NY, pp 519–527. https://doi.org/10.1145/3219819.3219829

Melacini M, Perotti S, Rasini M, Tappia E (2018) E-fulfilment and distribution in omni-channel retailing: a systematic literature review. Int Jnl Phys Dist Log Manage 48(4):391–414. https://doi.org/10.1108/IJPDLM-02-2017-0101

Mentzer JT, Kahn KB (1995) Forecasting technique familiarity, satisfaction, usage, and application. J Forecast 14(5):465–476. https://doi.org/10.1002/for.3980140506

Micol Policarpo L, da Silveira DE, da Rosa RR, Antunes Stoffel R, da Costa CA, Victória Barbosa JL, Scorsatto R, Arcot T (2021) Machine learning through the lens of e-commerce initiatives: an up-to-date systematic literature review. Comput Sci Rev 41:100414. https://doi.org/10.1016/j.cosrev.2021.100414

Miles MB, Huberman AM, Saldaña J (2020) Qualitative data analysis: A methods sourcebook. Sage, Los Angeles

National Retail Federation/Appriss Retail (2023) Consumer returns in the retail industry 2022. https://nrf.com/research/2022-consumer-returns-retail-industry . Accessed 23 May 2023

Ni J, Neslin SA, Sun B (2012) Database submission the ISMS durable goods data sets. Mark Sci 31(6):1008–1013. https://doi.org/10.1287/mksc.1120.0726

Page MJ, McKenzie JE, Bossuyt PM, Boutron I, Hoffmann TC, Mulrow CD, Shamseer L, Tetzlaff JM, Akl EA, Brennan SE, Chou R, Glanville J, Grimshaw JM, Hróbjartsson A, Lalu MM, Li T, Loder EW, Mayo-Wilson E, McDonald S, McGuinness LA, Stewart LA, Thomas J, Tricco AC, Welch VA, Whiting P, Moher D (2021) The PRISMA 2020 statement: an updated guideline for reporting systematic reviews. Syst Rev 10:89. https://doi.org/10.1186/s13643-021-01626-4

Pandya R, Pandya J (2015) C5.0 algorithm to improved decision tree with feature selection and reduced error pruning. IJCA 117(16):18–21. https://doi.org/10.5120/20639-3318

Petropoulos F, Apiletti D, Assimakopoulos V, Babai MZ, Barrow DK, Ben Taieb S, Bergmeir C, Bessa RJ, Bijak J, Boylan JE, Browell J, Carnevale C, Castle JL, Cirillo P, Clements MP, Cordeiro C, Cyrino Oliveira FL, de Baets S, Dokumentov A, Ellison J, Fiszeder P, Franses PH, Frazier DT, Gilliland M, Gönül MS, Goodwin P, Grossi L, Grushka-Cockayne Y, Guidolin M, Guidolin M, Gunter U, Guo X, Guseo R, Harvey N, Hendry DF, Hollyman R, Januschowski T, Jeon J, Jose VRR, Kang Y, Koehler AB, Kolassa S, Kourentzes N, Leva S, Li F, Litsiou K, Makridakis S, Martin GM, Martinez AB, Meeran S, Modis T, Nikolopoulos K, Önkal D, Paccagnini A, Panagiotelis A, Panapakidis I, Pavía JM, Pedio M, Pedregal DJ, Pinson P, Ramos P, Rapach DE, Reade JJ, Rostami-Tabar B, Rubaszek M, Sermpinis G, Shang HL, Spiliotis E, Syntetos AA, Talagala PD, Talagala TS, Tashman L, Thomakos D, Thorarinsdottir T, Todini E, Trapero Arenas JR, Wang X, Winkler RL, Yusupova A, Ziel F (2022) Forecasting: theory and practice. Int J Forecast 38(3):705–871. https://doi.org/10.1016/j.ijforecast.2021.11.001

Polikar R (2006) Ensemble based systems in decision making. IEEE Circuits Syst Mag 6(3):21–45. https://doi.org/10.1109/mcas.2006.1688199

Potdar A, Rogers J (2012) Reason-code based model to forecast product returns. Foresight 14(2):105–120. https://doi.org/10.1108/14636681211222393

Pur S, Stahl E, Wittmann M, Wittmann G, Weinfurtner S (2013) Retourenmanagement im Online-Handel–das Beste daraus machen: Daten, Fakten und Status quo. Ibi Research, Regensburg

Rajasekaran V, Priyadarshini R (2021) An e-commerce prototype for predicting the product return phenomenon using optimization and regression techniques. In: Singh M, Tyagi V, Gupta PK, Flusser J, Ören T, Sonawane VR (eds) Advances in computing and data sciences: proceedings of the 5th international conference on advances in computing and data sciences, 1st edn, vol 1441, pp 230–240. https://doi.org/10.1007/978-3-030-88244-0_22

Ravitch SM, Riggan M (2017) Reason and rigor: how conceptual frameworks guide research. Sage, Los Angeles, London, New Delhi, Singapore, Washington DC

Ren S, Chan H-L, Siqin T (2020) Demand forecasting in retail operations for fashionable products: methods, practices, and real case study. Ann Oper Res 291(1–2):761–777. https://doi.org/10.1007/s10479-019-03148-8

Rezaei M, Cribben I, Samorani M (2021) A clustering-based feature selection method for automatically generated relational attributes. Ann Oper Res 303(1–2):233–263. https://doi.org/10.1007/s10479-018-2830-2

Rogers DS, Lambert DM, Croxton KL, García-Dastugue SJ (2002) The returns management process. Int J Log Manag 13(2):1–18. https://doi.org/10.1108/09574090210806397

Röllecke FJ, Huchzermeier A, Schröder D (2018) Returning customers: the hidden strategic opportunity of returns management. Calif Manage Rev 60(2):176–203. https://doi.org/10.1177/0008125617741125

Sahoo N, Dellarocas C, Srinivasan S (2018) The impact of online product reviews on product returns. Inf Syst Res 29(3):723–738. https://doi.org/10.1287/isre.2017.0736

Samorani M, Ahmed F, Zaiane OR (2016) Automatic generation of relational attributes: an application to product returns. In: Proceedings of the 4th IEEE international conference on big data, pp 1454–1463

Santoro G, Fiano F, Bertoldi B, Ciampi F (2019) Big data for business management in the retail industry. MD 57(8):1980–1992. https://doi.org/10.1108/MD-07-2018-0829

Shaharudin MR, Zailani S, Tan KC (2015) Barriers to product returns and recovery management in a developing country: investigation using multiple methods. J Clean Prod 96:220–232. https://doi.org/10.1016/j.jclepro.2013.12.071

Shang G, McKie EC, Ferguson ME, Galbreth MR (2020) Using transactions data to improve consumer returns forecasting. J Oper Manag 66(3):326–348. https://doi.org/10.1002/joom.1071

Srivastava SK, Srivastava RK (2006) Managing product returns for reverse logistics. Int Jnl Phys Dist Log Manage 36(7):524–546. https://doi.org/10.1108/09600030610684962

Stock JR, Mulki JP (2009) Product returns processing: an examination of practices of manufacturers, wholesalers/distributors, and retailers. J Bus Logist 30(1):33–62. https://doi.org/10.1002/j.2158-1592.2009.tb00098.x

Stöcker B, Baier D, Brand BM (2021) New insights in online fashion retail returns from a customers’ perspective and their dynamics. J Bus Econ 91(8):1149–1187. https://doi.org/10.1007/s11573-021-01032-1

Sweidan D, Johansson U, Gidenstam A (2020) Predicting returns in men’s fashion. In: Proceedings of the 14th international fuzzy logic and intelligent technologies in nuclear science conference, pp 1506–1513. https://doi.org/10.1142/9789811223334_0180

Thaler RH, Sunstein CR (2009) Nudge: Improving decisions about health, wealth and happiness. Penguin

Tibben-Lembke RS, Rogers DS (2002) Differences between forward and reverse logistics in a retail environment. Supp Chain Mnagmnt 7(5):271–282. https://doi.org/10.1108/13598540210447719

Tibshirani R (1996) Regression shrinkage and selection via the lasso. J Roy Stat Soc: Ser B (Methodol) 58(1):267–288. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x

Toktay LB, van der Laan EA, de Brito MP (2004) Managing product returns: the role of forecasting. In: Dekker R, Fleischmann M, Inderfurth K, van Wassenhove LN (eds) Reverse logistics. Springer, Berlin, Heidelberg, pp 45–64. https://doi.org/10.1007/978-3-540-24803-3_3

Toktay LB, Wein LM, Zenios SA (2000) Inventory management of remanufacturable products. Manage Sci 46(11):1412–142. https://doi.org/10.1287/mnsc.46.11.1412.12082

Tranfield D, Denyer D, Smart P (2003) Towards a methodology for developing evidence-informed management knowledge by means of systematic review. Br J Manag 14(3):207–222. https://doi.org/10.1111/1467-8551.00375

Uman LS (2011) Systematic reviews and meta-analyses. J Can Acad Child Adolesc Psychiatry 20(1):57–59

Urbanke P, Kranz J, Kolbe L (2015) Predicting product returns in e-commerce: the contribution of mahalanobis feature extraction. In: Proceedings of the 14th international conference on computer and information science

Urbanke P, Uhlig A, Kranz J (2017) A customized and interpretable deep neural network for high-dimensional business data–evidence from an e-commerce application. In: Proceedings of the 38th international conference on information systems

Vakulenko Y, Shams P, Hellström D, Hjort K (2019) Service innovation in e-commerce last mile delivery: mapping the e-customer journey. J Bus Res 101:461–468. https://doi.org/10.1016/j.jbusres.2019.01.016

vom Brocke J, Simons A, Niehaves B, Reimer K, Plattfaut R, Cleven A (2009) Reconstructing the giant: on the importance of rigour in documenting the literature search process. In: Proceedings of the 17 th european conference on information systems

von Zahn M, Bauer K, Mihale-Wilson C, Jagow J, Speicher M, Hinz O (2022) The smart green nudge: reducing product returns through enriched digital footprints and causal machine learning. SSRN J. https://doi.org/10.2139/ssrn.4262656

Walsh G, Möhring M (2017) Effectiveness of product return-prevention instruments: empirical evidence. Electron Mark 27(4):341–350. https://doi.org/10.1007/s12525-017-0259-0

Walsh G, Möhring M, Koot C, Schaarschmidt M (2014) Preventive product returns management systems–a review and model. In: Proceedings of the 22nd european conference on information systems

Webster J, Watson RT (2002) Analyzing the past to prepare for the future: writing a literature review. MIS Q 26(2):xiii–xxiii

Winklhofer H, Diamantopoulos A, Witt SF (1996) Forecasting practice: a review of the empirical literature and an agenda for future research. Int J Forecast 12(2):193–221. https://doi.org/10.1016/0169-2070(95)00647-8

Wirth R, Hipp J (2000) CRISP-DM: towards a standard process model for data mining. In: Proceedings of the 4th international conference on the practical applications of knowledge discovery and data mining, vol 1, pp 29–40

Zhao X, Hu S, Meng X (2020) Who should pay for return freight in the online retailing? Retailers or consumers. Electron Commer Res 20(2):427–452. https://doi.org/10.1007/s10660-019-09360-9

Zhu Y, Li J, He J, Quanz BL, Deshpande A (2018) A local algorithm for product return prediction in e-commerce. In: Proceedings of the 27th international joint conference on artificial intelligence, pp 3718–3724. https://doi.org/10.24963/ijcai.2018/517

Zotteri G, Kalchschmidt M (2007) Forecasting practices: empirical evidence and a framework for research. Int J Prod Econ 108(1–2):84–99. https://doi.org/10.1016/j.ijpe.2006.12.004

Download references

Open Access funding enabled and organized by Projekt DEAL. The authors have not disclosed any funding.

Author information

Authors and affiliations.

Chair of Operations Management and Logistics, University of Bamberg, Feldkirchenstr. 21, 96052, Bamberg, Germany

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to David Karl .

Ethics declarations

Conflict of interest.

The authors declare that no funds, grants, or other support were received during the preparation of this manuscript. The authors have no relevant financial or non-financial interests to disclose. The data that support the findings of this study are available from the corresponding author upon request.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: Author-centric content summary (with focus on forecasting issues)

1.1 journal publications.

Hess and Mayhew ( 1997 ) describe a forecasting approach, taking the example of a direct marketer for apparel with a lenient consumer return policy (free returns anytime). The analysis can plausibly be applied to a general retailer, although return time windows are somewhat different. A regression approach and a hazard model are compared. The regression approach itself is split into an OLS estimation of return timing (with poor fit) and a logit model of return propensities, which is in turn used for the split function of the box-cox-hazard approach for estimating the probability of a return over time. The accuracy was measured by fit statistics regarding the absolute deviation from the actual cumulative return proportion, with the split-hazard model outperforming the regression model. Besides price, the importance of fit of the respective product is used as a predictor.

Potdar and Rogers ( 2012 ) propose a method using reason codes combined with consumer behavior data for forecasting returns volume in the consumer electronics industry, aiming at the retailer stage as well as the preceding supply chain stages. The subject of their study is an offline retailer, which allows generalization for e-tailers due to a similar return policy (14 days free returns with no questions asked). In a multi-step approach, the authors are using essential statistical methods (moving averages, correlations, and linear regression), but use sophisticated domain and product knowledge like product features or price in relation to past return numbers, aiming to rank different competing products regarding their quality, and to predict the volume of returns for a given product for each given period of time.

Fu et al. ( 2016 ) derive a framework for the forecasting of product- and consumer-specific return propensities, i.e., the return propensity for individual purchases. Their study is directed at online shopping and is evaluated using the data from an online cosmetic retailer selling via Taobao.com. The predictors are categorized into inconsistencies in the buying and in the shipping phase of a transaction. A latent factor model is introduced for return propensities capturing differences between expectations and performance. This model is extended by product (e.g., warranty) and customer information (e.g., gender, credit score). The model is based on conditional probabilities, and an iterative expectation–maximization approach derives its parameters. MAE and RMSE, precision/recall, and AUC metrics assess the forecast accuracy. As benchmark models, two matrix factorization models and two memory-based models (historical consumer or product return rates) are compared, while the proposed model outperforms the references. Furthermore, this model allows identifying various return reasons, e.g., return abuse and fraud.

Building on the work of Fu et al. ( 2016 ), Li et al. ( 2019 ) investigate underlying reasons for consumer returns, taking the example and data of an online cosmetic retailer via Taobao.com. They examine the customers’ return propensity for product types, aiming at detecting abnormal returns suspecting abuse. Different from purchase decisions, they find customer profile data to be more important predictors for return decisions than product information or transaction details. The authors detect “selfish” or “fraud” consumers based on this rationale. For estimating return propensities for a given consumer and product, they calculate the return behavior depending on the return decision of similar consumers (“trust network”) and the amount of trust in these other consumers. MAE and precision-recall-measures are used to assess the prediction of different random walk models. The employed trust-based random walk model outperforms the other models on most indicators, building the basis for anomaly detection of consumers to cluster them into groups (honest/selfish/fraud) and individually address the return issues of these groups.

Although the paper from Cui et al. ( 2020 ) aims at product return forecasts from the perspective of the manufacturer, their case can be generalized for classic e-tailers, as the manufacturer is responsible for the return handling in their scenario—a task often performed by the retailer. They used a comprehensive data set from an automotive accessories manufacturer aiming to forecast return volume for sales channels and different products. The observed return rates lower than 1% are uncommonly low, and therefore the results must be interpreted with caution. First, a hierarchical OLS regression step-by-step incorporates up to 40 predictors regarding sales, time, product type, sales channel, and product details, including return history. The full model shows a significantly increased performance measured by a more than 50% decrease of MSE, which was used as the primary performance measure. Interestingly, relatively small differences in model quality (R 2 ) led to overproportional changes in the MSE. Using a machine-learning approach for predictor selection (“LASSO”), another MSE reduction of about 10% was achieved. Data Mining approaches (random forest, gradient boosting) could not outperform the LASSO approach. Forecasting performance was strongly dependent on the variation of the data. The two best predictors for return volume were past sales volume and lagged return statistics. The authors were wondering about the importance of lagged return information, failing to acknowledge that this predictor includes the consumer reaction to detailed product information, which has not been a significant predictor.

Ketzenberg et al. ( 2020 ) segment customers and target detecting the small number of abusive returners, as these are unprofitable for the retailer and generate significant losses over a long time. In general, high-returning customers are usually more profitable. The data used for this study is from a department store retailer with various product groups in the assortment. Predictors are transactional data and customer attributes. For classification, different algorithms like logit, Support Vector Machines (SVM), Random Forests (RF), Neural Networks (NN) are used in combination with different shrinkage methods like LASSO, ridge regression, and elastic net. Random Forests and especially Neural Networks outperform the other algorithms, assessed by sensitivity, precision, and AUC. In conclusion, a low rate of false positives could assure retailers of using abuse detection systems.

Shang et al. (Shang et al. 2020 ) developed a predict-aggregate (P-A) model adaptable both for retailers and manufacturers for forecasting return volume in a continuous timeframe, in contrast to commonly used aggregate-predict (A-P) models. Instead of aggregating data first (i.e., sales volume and returns volume), they first aggregate product-specific return probabilities and then aggregate the purchases by addition of the individual probabilities. As predictors, they only use timestamps and lagged return information. They tune and assess their models on two datasets from an offline electronics and an online jewelry retailer. ARIMA and lagged return models known from end-of-life forecasting (de Brito et al. 2005 ) are used as benchmarks, using RMSE as an assessment criterion. The authors show that even a basic version of their approach outperforms the benchmark models in almost all observed cases by up to 19%, though using only lagged returns and timestamps as input. Different extensions, e.g., including more predictor variables, can easily be integrated and are shown to further improve the forecasting performance.

John et al. ( 2020 ) try to predict the rare event of return fraud from customer representatives that make use of exactly knowing the e-commerce company’s return policy framework and buying and returning items fraudulently. Therefore, predictors range from transaction details to customer service agent attributes. A penalized likelihood logit model was chosen by the authors and was evaluated by precision and recall, focussing on maximizing recall and minimizing false negatives. The most important predictors were communication type and reason for interaction.

The paper by Rezaei et al. ( 2021 ) introduces a new algorithm to automatically select attributes from high-dimensional databases for forecasting purposes. As a demonstration sample, they use simulated data as well as the publicly available ISMS Durable Goods dataset (Ni et al. 2012 ) for consumer electronics. The results are assessed by AUC, precision, recall, and f1-score. They compare different configurations. For the simulated data, LASSO as shrinkage method generally works best, outperforming RF and BaggedTrees. For real-world data, based on a forecast with a logit model, they show that the proposed selection algorithm performs similar or better compared to LASSO, SVM, and RF, while the complexity of the chosen variables is lower.

1.2 Conference publications

Urbanke et al. ( 2015 ) describe a decision support system to better direct return-reducing interventions at e-commerce purchases with highly likely returns. They compare different approaches for extracting input variables for return propensity forecasting. They use a large dataset from a fashion e-tailer, aiming to reduce the input variables regarding consumer profile, product profile, and basket information from over 5,000 binary variables to 10 numeric variables by different algorithms (e.g., principal component analysis, non-negative matrix factorization, etc.). The results are then used to predict return propensities with a wide variety of state-of-the-art algorithms (AdaBoost, CART, ERT, GB, LDA, LR, RF, SVM), thus also revealing both feature selection and prediction performance. The proposed Mahalanobis feature extraction algorithm used as input for AdaBoost outperforms all other combinations presented, while interestingly, a logit model with all original inputs delivers relatively precise forecasts.

Building on some parts of this study, the paper of Urbanke et al. ( 2017 ) presents a return decision forecasting approach and aims at two targets, (1) high predictive accuracy and (2) interpretability of the model. Based on real-world data of a fashion and sports e-tailer, they first hand-craft 18 input variables and then use NN to extract more features and compare this approach to other feature extraction algorithms based on different forecasting algorithms. For assessment, they measure correlations between out-of-sample-predictions and class labels and AUC. The best performing classifier was AdaBoost, while the contribution of NN-based feature extraction shows interpretability as well as superior predictive performance.

Ahmed et al. ( 2016 ) focus on the automatic aggregation and integration of different data sources to generate input variables (features). They use return forecasting just as an exemplary classification problem for their data preparation approach, using various ML algorithms, e.g., RF, NN, DT-based algorithms, to detect returned purchases of an electronics retailer. Based on AUC measure, the results of their GARP-approach are superior to not using aggregations while generating an extensive amount of features with no pruning approach. In general, SVM and RF work best in combination with the proposed GARP approach. The data is based on the publicly available ISMS durable goods data sets (Ni et al. 2012 ).

A similar group of authors published another paper (Samorani et al. 2016 ), again using the aforementioned ISMS dataset as an example for data preparation and automatic attribute generation. Besides forecasting performance, in this paper, they want to generate knowledge about important return predictors; e.g., a higher price is associated with more returns, but only as long price levels are below a 1,500$ threshold. AUC is used to assess different levels of data integration, confirming that overfitting might happen when too many attributes are used.

Heilig et al. ( 2016 ) describe a Forecasting Support System (FSS) to predict return decisions in a real environment. First, they compare different forecasting approaches for data from a fashion e-tailer, assessed by AUC and accuracy metrics. The ensemble selection approach outperforms all other classifiers, with RF being the closest competitor. Computational times grow exponentially when using more data. Based on these results, they secondly describe a cloud framework for implementing such ensemble models for live use in a real shop environment.

Ding et al. ( 2016 ) present an approach to predict the daily return rate of an e-commerce company based on sentiment analysis of tweets regarding this company in the categories of news, experience, products, and service. Therefore, they use sophisticated text mining technologies, while the forecasting approach of an econometric vector autoregression is more or less common. The emotion of posts regarding different variables (news, product, service) impacts the returns rate negatively, while the emotion of purchasing experience impacts it positively, showing that the prediction accuracy enhances through classifying social network posts.

Drechsler and Lasch ( 2015 ) aim at forecasting the volume of fraudulent returns in e-commerce over several periods of time. They present different approaches multiplying the sales volume and the relative return rate, the first referring to Potdar and Rogers ( 2012 ), estimating the rate of misused returns directly based on time-lag-specific return rates. In a second approach referring to Toktay et al. ( 2000 ), they estimate the overall returns rate and multiply it by the time-specific ratio of fraudulent returns. The return rates were forecasted by moving averages and exponential smoothing techniques. Assessment criteria for performance comparison based on simulated data were MAE, MAPE, and TIC, showing the first approach to be superior, but both methods are not sufficiently robust. Therefore, the authors include further time-specific information (like promotions or special events, which could foster fraudulent returns) in a model using a Holt-Winters approach, showing superior performance. All of the models are highly dependent on low fluctuation in return rates, showing a shortcoming of these more or less naive forecasting techniques.

Asdecker and Karl ( 2018 ) compare the performance of different algorithms for forecasting binary return decisions: logit, linear discriminant analysis, neuronal networks, and a decision-tree-based algorithm (C5.0). Their analysis is based on the data of a fashion e-tailer, including price, consumer information, and shipment information (number of articles in shipment, delivery time). For the assessment of different algorithms, they use the total absolut error (TAE) and relative error. An ensemble learning approach performs best and similar to the C5.0 algorithm. Though, differences in performance are relatively small, while only about 68% of return decisions are forecasted correctly.

Li et al. ( 2018 ) propose a hypergraph representation of historical purchase and return information combined with a random-walk-based local graph cut algorithm to forecast return decisions on order (basket) level as well as on product level. By this, they aim to detect the underlying return causes. They use data from two omnichannel fashion e-tailers from the US and Europe to assess the performance of their approach, using precision/recall/F 0.5 /AUC metrics while arguing that precision is the most important indicator for targeted interventions. Three similarity-based approaches (e.g., a k-Nearest Neighbor model) are used as reference. The proposed approach performs best regarding AUC, precision, and F 0.5 metrics.

Zhu et al. ( 2018 ) developed a weighted hybrid graph algorithm representing historical customer behavior and customer/product similarity, combined with a random-walk-based algorithm for predicting customer/product combinations that will be returned. They report an experiment based on data from a European fashion e-tailer suffering from return rates as high as 50%. For assessment, they use precision, recall, and F 0.5 metrics. Their approach is superior to two reference competitors (similarity-based and a bipartite graph algorithm). As predictors, they use product similarities and historical return information, while their approach can be enriched with detailed customer attributes.

Joshi et al. ( 2018 ) model the return decisions based on the data of an Indian e-commerce company, especially dealing with returns for apparel due to fit issues. In a two-step approach, they first model return probabilities using concepts from network science based on a customer’s historical purchase and return decisions, and secondly use a SVM implementation with return probabilities as a single input to classify for the return decision. Assessed by F 1 /precision/recall scores, their approach is superior to a reference random-walk baseline model.

Imran and Amin ( 2020 ) compare different forecasting algorithms (XGBoost, CatBoost, LightGBM, TabNet) for return classification based on the data of a general e-commerce retailer from Bangladesh. As input variables, only order attributes, including payment method and order medium, are used. For evaluation, they use metrics like true negative rate, false-positive rate, false-negative rate, true positive rate, AUC, F 2 -score, precision, and accuracy. In the end, they chose TPR, AUC, and F 2 -score, claiming that misclassifying high return probability objects were the first thing to avoid. According to these metrics, TabNet as a deep learning algorithm outperforms the other models. The most important predictors were payment method, order location, and promotional orders.

As returns are most prominent in fashion e-commerce, most of the forecasting papers take this industry as an example, as forecasting models are more precise when returns are more frequent. Hofmann et al. ( 2020 ) develop a more generalized order-based return decision forecasting approach, appropriate for different industries and suitable also for low return rates. For their analysis, they use a dataset from a german technical wholesaler with a return rate as low as 5%. Input variables were just basket composition and return information. For assessment, they used precision and recall metrics. RF did not perform superior to a statistical baseline approach, nor with oversampling as data preparation, to deal with the group imbalance. The DART algorithm makes use of the group imbalance correction by random oversampling. In general, gradient boosting performs best with imbalanced groups, also without oversampling, but forecasting quality is lower than with more specialized forecasting approaches as described for fashion. Furthermore, results were more accurate on basket level than on single-item level.

Fuchs and Lutz ( 2021 ) use Design Science Research (DSR) principles to design a meta-model for the real-time prediction of returns. The goal is to influence consumer decisions by triggering a feedback system based on the basket composition and its return probability. For forecasting, which is not the primary focus of their paper, they build upon a gradient boosting model taken from existing research (Hofmann et al. 2020 ) and describe possible implementations into an ERP system regarding asynchronous communication requirements and possible architecture.

The paper by Sweidan et al. ( 2020 ) evaluates the forecasting performance of a random forest model for a shipment-based return decision, using real-world data of a fashion e-tailer. For their model, they use customer (e.g., lagged return rate) and order information as inputs. They find that predictions with high confidence are very precise (i.e., low false-positive rate). Thus, interventions can be targeted at such orders already when the items are in the consumers’ basket without risk of a misdirected intervention. For assessment, accuracy, AUC, precision, recall and specificity are used. Regarding the predictors, they note that selection orders (a product in different sizes) are the best predictor for order-based returns.

Rajasekaran and Priyadarshini ( 2021 ) develop a metaheuristic for forecasting the product-based return probabilities. In the first step, they determine return probabilities based on product feedback, time, and product attributes regarding manufacturer return statistics. Secondly, they compare different algorithms (OLS, RF, Gradient Boosting) by MAE, MSE, and RMSE metrics. Interestingly, linear regression performs best in all metrics, but no explanation and a misinterpretation regarding the best algorithm are given.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Karl, D. Forecasting e-commerce consumer returns: a systematic literature review. Manag Rev Q (2024). https://doi.org/10.1007/s11301-024-00436-x

Download citation

Received : 24 August 2023

Accepted : 12 April 2024

Published : 21 May 2024

DOI : https://doi.org/10.1007/s11301-024-00436-x

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Consumer returns
• Product returns
• Forecasting
• Literature review

JEL classification

• Find a journal
• Publish with us
• Track your research