problem solving model division

Number Sense

Understanding numbers, their relationships and numerical reasoning

Using symbols to solve equations and express patterns

Studying shapes, sizes and spatial relationships in mathematics

Measurement

Quantifying and comparing attributes like length, weight and volume

Performing mathematical operations like addition, subtraction, division

Probability and Statistics

Analyzing uncertainty and likelihood of events and outcomes

Calculator Suite

Exploring functions, solving equations, constructing geometric shapes

Graphing Calculator

Visualizing equations and functions with interactive graphs and plots

Exploring geometric concepts and constructions in a dynamic environment

3D Calculator

Graphing functions and performing calculations in 3D

Scientific Calculator

Performing calculations with fractions, statistics and exponential functions

Exploring apps bundle including free tools for geometry, spreadsheet and CAS

Learn and practice division skills and improve your understanding of dividing numbers and solving division problems with interactive resources from GeoGebra.

Upper Elementary

Division models.

Model division in a variety of ways including sharing equally, repeated subtraction, rectangular arrays, and the relationship with multiplication.

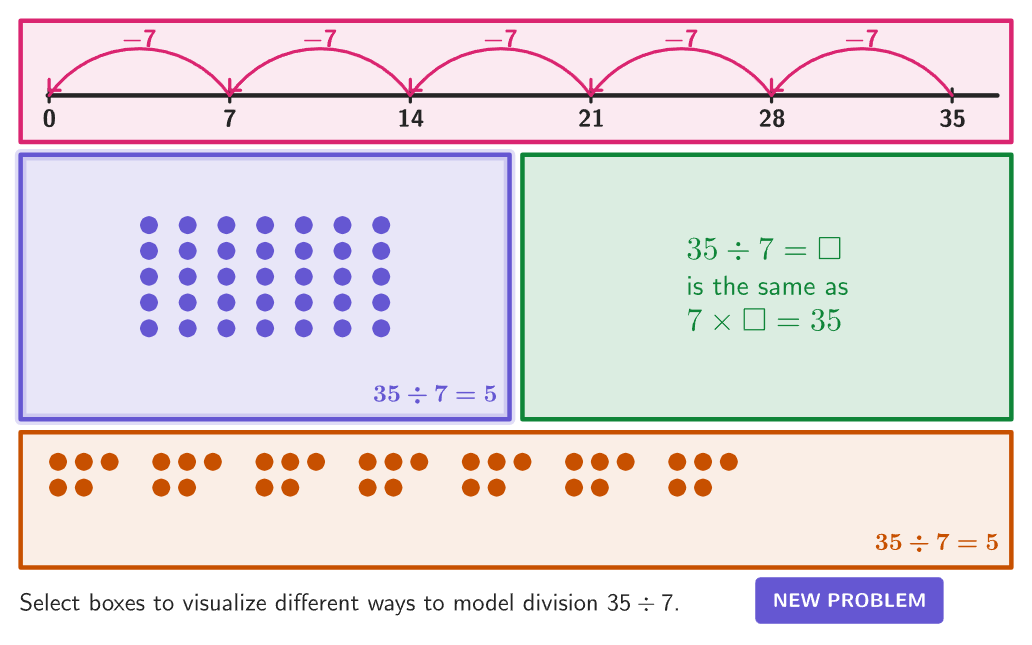
Creating Division Equations Using Visual Models

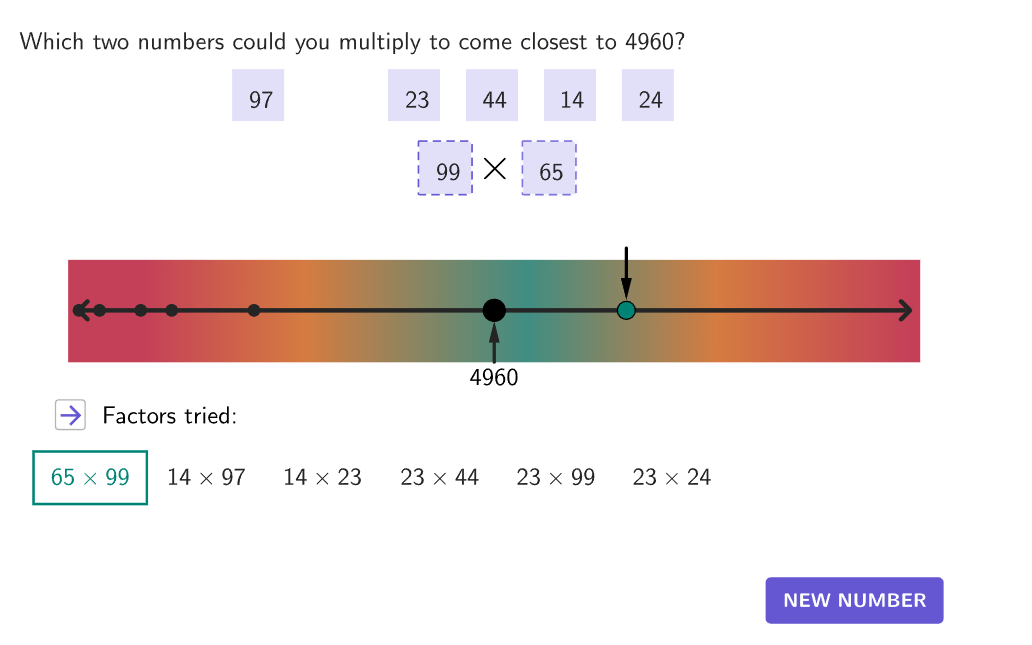
Estimating products and quotients.

Apply appropriate types of estimation for number and word problems that include estimating products and quotients.

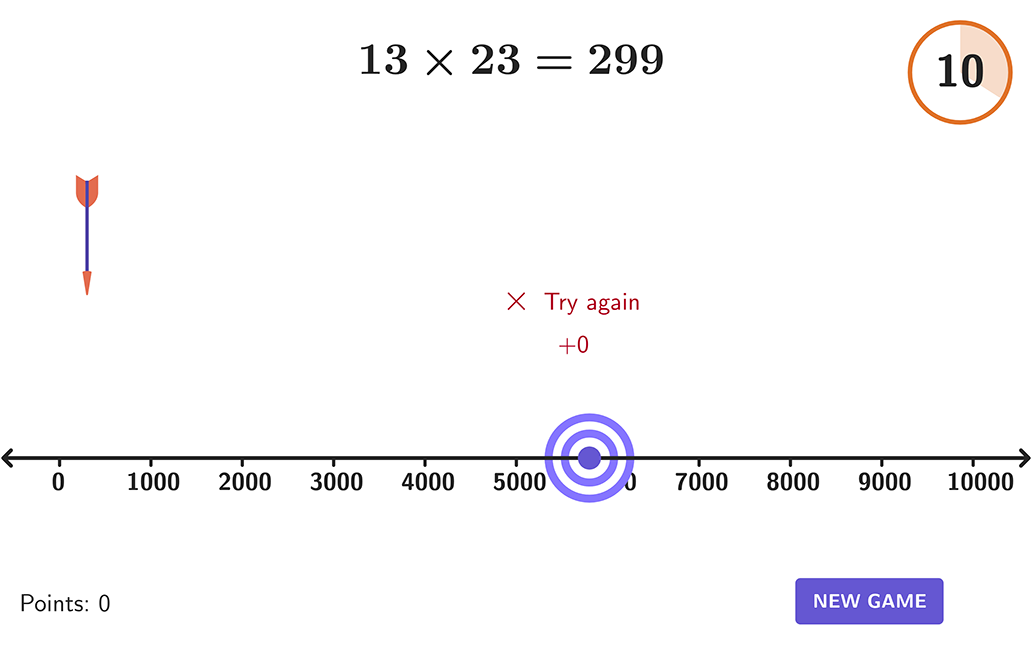
Multiplication and Division Estimation Game

Estimating quotients of whole numbers.

Estimate and solve division problems with multi-digit divisors; explain solution.

Estimating Products of 2-digit Numbers

Interpreting remainders.

Use remainders in problem-solving situations and interpret the remainder with respect to the original problem.

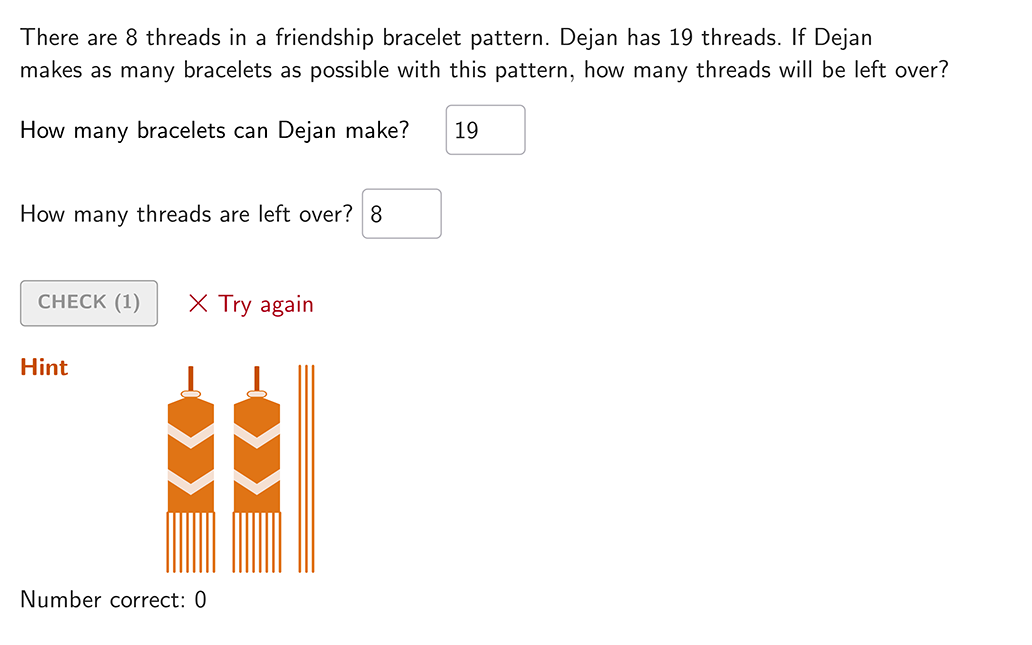
Division Problems with Remainders

Long division.

Divide using single-digit divisors with and without remainders.

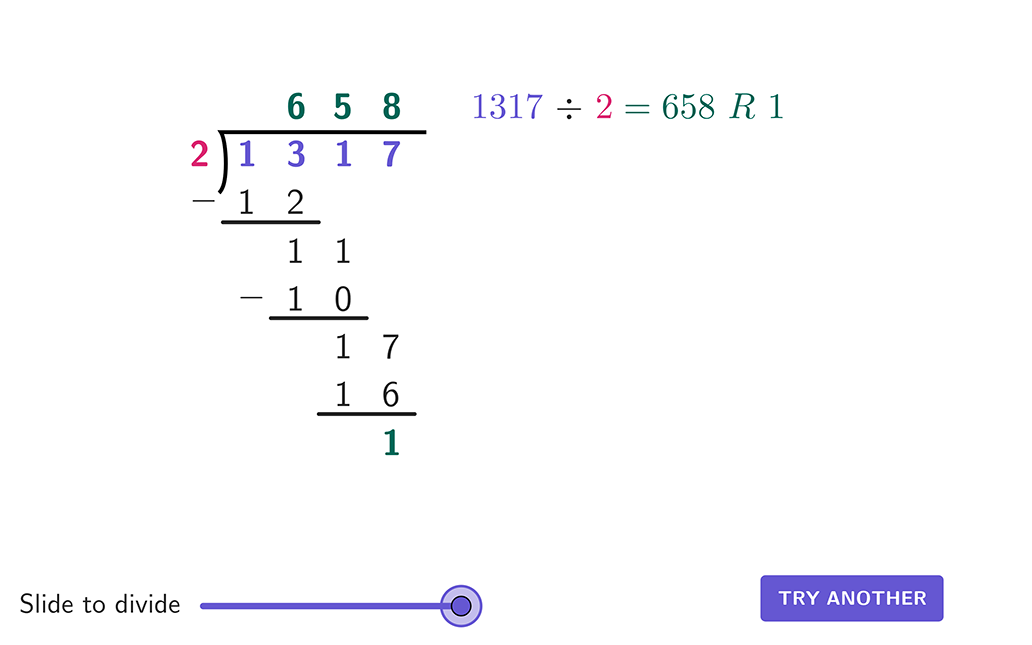
Long Division With One-Digit Divisors and Remainders

Multiplication and division sentences.

Write a multiplication or a division sentence to represent a number or word problem; solve.

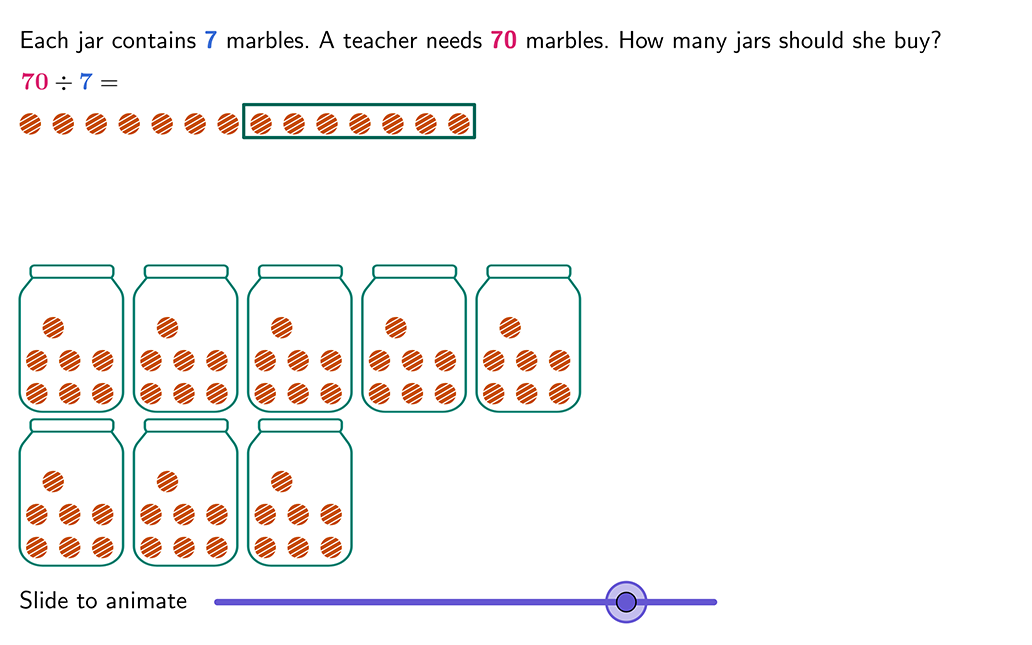
Division Word Problems

Multiplying and dividing by powers of 10.

Recognize and use patterns in powers of ten (with or without exponents) to multiply and divide whole numbers and decimals.

Multiplication and Division with Multiples of Powers of Ten

Middle school, multiplying and dividing integers.

Model or compute with integers using multiplication or division in number and word problems.

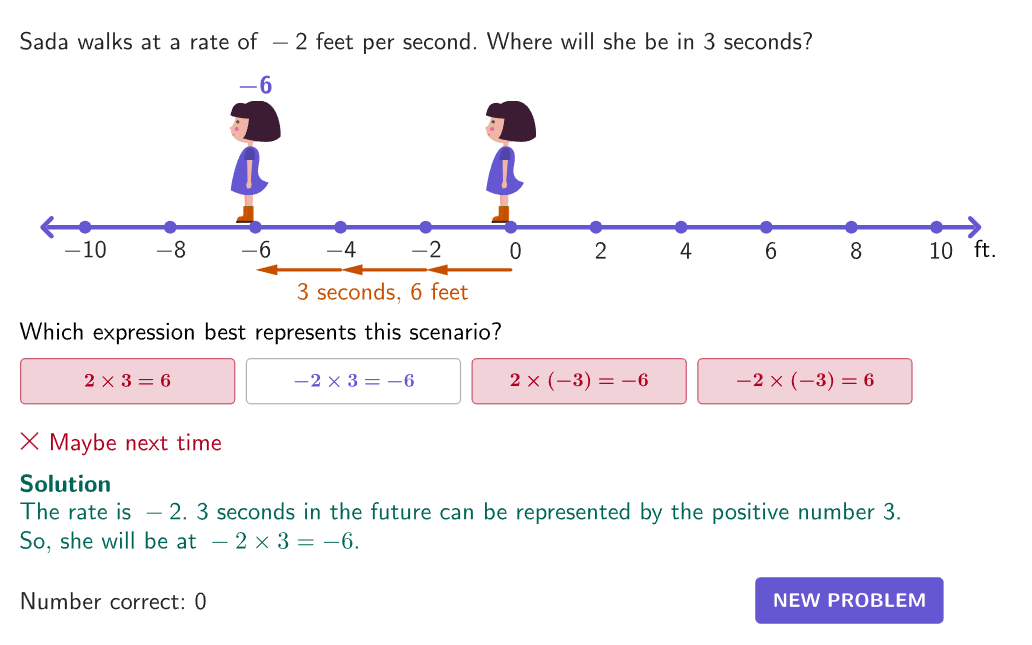
Multiplying Negative Numbers

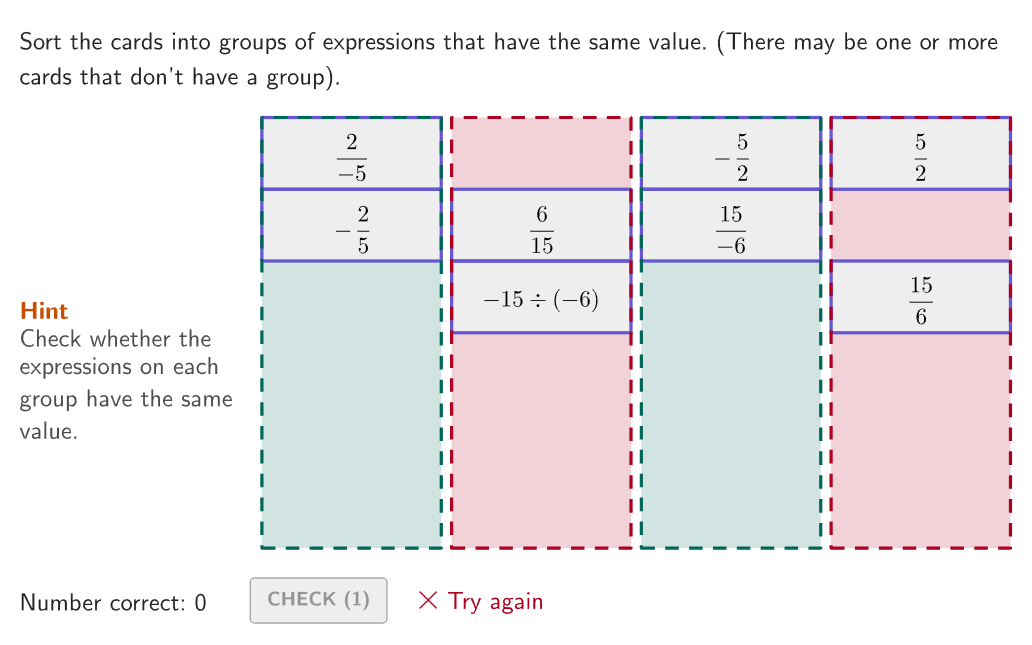
Card Sort: Multiplying and Dividing Integers

Community Resources

Explore an extensive collection of over one million math and science activities, exercises and lessons meticulously crafted by our global GeoGebra community. Immerse yourself in the boundless possibilities that await you.

An illustration depicting an interconnected network of users around the globe

Get started using GeoGebra today

Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others

Subtraction
Multiplication
Place Holder
Excess Value
Repeated Variable
Constant Difference
Constant Quantity
Contant Total
Kindergarten Math
Grade 1 Math
Grade 2 Math
Grade 3 Math
Grade 4 Math
Grade 5 Math
Grade 6 Math
Math Coaching Class - Master the Model Method in Singapore Math
Singapore Math
Testimonials
Kids Math Blog
Great Math Sites
Useful Links
Webinar-On-Demand
Live Webinars

Basic Division Model

Would you prefer to share this page with others by linking to it?

Click on the HTML link code below.
Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Home |
About |
Contact Us |
Privacy |
Newsletter |
Shop |
🔍 Search Site
Easter Color By Number Sheets
Printable Easter Dot to Dot
Easter Worksheets for kids
Kindergarten
All Generated Sheets
Place Value Generated Sheets
Addition Generated Sheets
Subtraction Generated Sheets
Multiplication Generated Sheets
Division Generated Sheets
Money Generated Sheets
Negative Numbers Generated Sheets
Fraction Generated Sheets
Place Value Zones
Number Bonds
Addition & Subtraction
Times Tables
Fraction & Percent Zones
All Calculators
Fraction Calculators
Percent calculators
Area & Volume Calculators
Age Calculator
Height Calculator
Roman Numeral Calculator
Coloring Pages
Fun Math Sheets
Math Puzzles
Mental Math Sheets
Online Times Tables
Online Addition & Subtraction
Math Grab Packs
All Math Quizzes
1st Grade Quizzes
2nd Grade Quizzes
3rd Grade Quizzes
4th Grade Quizzes
5th Grade Quizzes
6th Grade Math Quizzes
Place Value
Rounding Numbers
Comparing Numbers
Number Lines
Prime Numbers
Negative Numbers
Roman Numerals
Subtraction
Add & Subtract
Multiplication
Fraction Worksheets
Learning Fractions
Fraction Printables
Percent Worksheets & Help
All Geometry
2d Shapes Worksheets
3d Shapes Worksheets
Shape Properties
Geometry Cheat Sheets
Printable Shapes
Coordinates
Measurement
Math Conversion
Statistics Worksheets
Bar Graph Worksheets
Venn Diagrams
All Word Problems
Finding all possibilities
Logic Problems
Ratio Word Problems
All UK Maths Sheets
Year 1 Maths Worksheets
Year 2 Maths Worksheets
Year 3 Maths Worksheets
Year 4 Maths Worksheets
Year 5 Maths Worksheets
Year 6 Maths Worksheets
All AU Maths Sheets
Kindergarten Maths Australia
Year 1 Maths Australia
Year 2 Maths Australia
Year 3 Maths Australia
Year 4 Maths Australia
Year 5 Maths Australia
Meet the Sallies
Certificates

Division Worksheets ÷ Hub Page

Welcome to our Division Worksheets hub page.

Here you will find links to our many division worksheet pages, including division facts worksheets, division word problems and long division worksheets.

We also have other division resources including flashcards, division games and online division practice.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

This page contains links to other Math webpages where you will find a range of activities and resources.
If you can't find what you are looking for, try searching the site using the Google search box at the top of each page.

Division Learning

Division is often a process which kids often find quite difficult and hard to learn. Kids need to learn what division is before they start formal work on dividing numbers.

Sharing things out, such as counters, between pretend people or cuddly toys is a great way to start your child on their division journey so that they have a basic understanding of what division is. Putting counters into same-size groups is also another way to reinforce division as a model for both sharing and grouping.

When your child is confident with sharing and they have a good understanding of division, they can start learning their division facts and the long division method.

Once they have mastered long division dividing numbers by a single digit, they can start dividing numbers by 2 digits, and begin to learn to divide decimal numbers.

Quicklinks to:

Division Worksheets by Grade

Understanding Division
Online Division Practice

Division Facts Worksheets

Long Division Worksheets & Support
Dividing Negative Numbers

Division Word Problems

Division Resources
Division Games

Second Grade Division

The link below will open the 2nd-grade-math-salamanders website in a new browser window.

How to do Division Worksheets
2nd Grade Division Problems
Second Grade Division Worksheets

3rd Grade Division

Division Facts to 10x10 Worksheets
Long Division Worksheets 3rd Grade
Division Worksheets Grade 3 Word Problems

4th Grade Division

Divding by Multiples of 10 and 100 Worksheets
4th Grade Long Division Worksheets
Division Worksheets Grade 4 Word Problems

5th Grade Division

Decimal Division Facts
Long Division Worksheets (whole numbers)
Long Division of Decimal Numbers

Understanding Division Worksheets

Here you will find a selection of Division sheets designed to help your child improve their understanding of what division is.

The sheets introduce the idea of division in terms of sharing and grouping, and designed to be a good practical start to learning about division.

All the free math work sheets in this section are informed by the Elementary Math Benchmarks for 2nd Grade.

Understanding Division Sheets

Division Flashcards

Here you will find a selection of Division Flashcards designed to help your child learn their Division facts.

Using flashcards is a great way to learn your Math facts. They can be taken on a journey, played with in a game, or used in a spare five minutes daily until your child knows their facts off by heart.

Using these flashcards will help your child to:

learn their division facts up to 10x10.

All the free Math flash cards in this section are informed by the Elementary Math Benchmarks for 3rd Grade.

Printable Math Flashcards - Division

Multiplication & Division Times Table Charts

Here you will find a selection of Multiplication/Division Times Table Charts to 10x10 or 12x12 to support your child in learning their multiplication and division facts.

There is a wide selection of multiplication charts including both color and black and white, smaller charts, filled charts and blank charts.

Using these charts will help your child to:

Learn their multiplication and division facts to 10x10 or 12x12;
Large Multiplication Chart
Times Tables Chart to 10x10
Times Table Grid to 12x12

Division Practice Area

Here is our free division practice area.

If you want to practice your division facts, or take a timed division test, then this is the place for you.

In this area, we cover the following division facts:

division facts up to 5x5, up to 10x10 or up to 12x12;
division facts linked to individual tables facts;
dividing by 10 and 100.
Division Practice Zone

Here you will find a selection of Mental Division sheets designed to help your child improve their recall of Division Facts and to apply their facts to answer related questions.

Division (and multiplication) Worksheet Generator

Here is our free generator for division (and multiplication) worksheets.

This easy-to-use generator will create randomly generated division worksheets for you to use.

Each sheet comes complete with answers if required.

The areas the generator covers includes:

Dividing with numbers to 5x5;
Dividing with numbers to 10x10;
Dividing with numbers to 12x12;
Divide with 10s e.g. 120 ÷ 4
Divide with 100s e.g. 2100 ÷ 3
Divide with tenths e.g. 2.4 ÷ 6
Dividing with a single times table;
Practicing division with selected times tables;

These generated sheets can be used in a number of ways to help your child with their division table learning.

Division Facts Worksheets (randomly generated)
Multiplication & Division Worksheets (randomly generated)

Division Facts to 10x10 Sheets (3rd & 4th Grade)

Here you will find a selection of Division sheets designed to help your child learn their Division facts up to 10x10.

Example: if a child knows that 5 x 4 = 20, then they should also know that 20 ÷ 5 = 4 and 20 ÷ 4 = 5.

The sheets are graded so that the division facts start off up to 5x5, progressing on to 10x10 by the end.

Using these sheets will help your child to:

understand how division and multiplication are related;
Printable Division Worksheets to 10x10

Division Related Facts 10s and 100s (4th & 5th Grade)

Here you will find a selection of Division sheets designed to help your child learn to use their Division facts up to 10x10 to answer related questions.

Example: if you know that 42 ÷ 6 = 7, then you also know that 420 ÷ 6 = 70 or 420 ÷ 70 = 6, etc.

The sheets are graded so that the related division facts start off easier, then get gradually harder.

know how to multiply and divide decimals up to 3dp by 10 or 100;
apply their division facts up to 10x10 to answer related questions.
Multiply and Divide by 10 100 (decimals)

Division Related Facts Decimals (5th & 6th Grade)

Here you will find a selection of Division sheets designed to help your child learn to use their Division facts up to 10x10 to answer related questions involving decimals.

Example: if you know that 24 ÷ 6 = 4, then you also know that 2.4 ÷ 6 = 0.4 or 2.4 ÷ 0.4 = 6, etc.

apply their division facts up to 10x10 to answer related questions involving decimals.

Dividing Negative Numbers (6th Grade)

We also have a generator for creating your own division worksheets involving signed integers.

You can choose the values you want and tailor the worksheets to your needs.

Dividing Negative Numbers (randomly generated)

Long Division Worksheets and Support

Long Division starts properly once kids reach 3rd grade, and after they have a good understanding of what division is, and know their division facts.

Here you will find long division worksheets, starting from dividing a 2 digit number by a single digit, all the way up to dividing a 3 or 4 digit number by two digits.

Long Division Support

We have created a calculator to help you master the long division method.

Just type in the dividend and divisor and let the calculator show you how to work out the long division, step-by-step.

The calculator also gives commentary to show you what is happending at each stage.

$Step by step long division calculator image$

Step by Step Long Division Calculator

Quickinks to ...

3rd Grade Long Division
4th Grade Long Division
5th Grade Long Division
6th Grade Long Division

Randomly Generated Long Division Problems Worksheet Generator

Take a look at our long division problems worksheet generators.

This generator will generate your own worksheets from 2-digits by 1-digit to 5-digits by 2-digits.

You can also create your own long division worksheets with money amounts from up to $10 by a single digit to up to $100,000 by 2-digits

You can choose to have remainders or not, and whether to record the remainders as a whole number or fraction.

Long Division Problems with Answers (randomly generated)
Long Division with Money (randomly generated)

Long Division 2 Digits by 1 Digit (3rd Grade)

Here you will find a selection of free Division sheets 3rd Grade which are designed to help your child understand how to do long division. The sheets are graded so that the easier ones are at the top.

divide a 2 digit number by a single digit;
use remainders when dividing.

Long Division 3 & 4 Digits by 1 Digit (4th Grade)

Here you will find a range of Long Division sheets which are designed to help your child master their Long Division by a single digit.

use long division to divide a range of numbers by a single digit.

Long Division by 2 Digits (5th Grade)

Here you will find a selection of free Division sheets designed to help your child learn to do 2 digit long division. The sheets are graded so that the easier ones are at the top.

divide a range of 3,4 and 5 digit numbers by two digits.
Long Division Worksheets - Dividing by 2 Digits

Long Division by Decimals (6th Grade)

We have some decimal division worksheets with up to 3 decimal places.

There are also some worked examples to show you how.

We have created lots of division word problems for you to solve.

The sheets involve solving division problems in a range of different contexts and involve both sharing and grouping.

These sheets involve solving a range of division problems.

Using this link will open our 2nd Grade Math Salamanders website in a new browser window.

2nd Grade Division Worksheets
Division Sheets Grade 3 Word Problems
Division Sheets Grade 4 Word Problems

Fun Division Games

Here you will find a range of Free Printable Division Games.

The following games develop the Math skill of dividing in a fun and motivating way.

The following sheets will help your child to:

learn their Division facts;
develop their strategic thinking skills.

All the printable Math sheets in this section are informed by the Elementary Math Benchmarks.

Math Division Games

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

$math salamanders news image$

Newsletter Signup

Return from Division Worksheets page to Math Salamanders Home Page

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

Teaching Area Model Division to 4th Graders

Learning long-division can be challenging for fourth graders. Luckily, there’s the area model division (4th grade) to the rescue! Also referred to as the Box Method, this is a great method for children to become fluent in long division.

So if you’re wondering how to teach area model division to your 4th-grade students, we’ve complied several tips that will get you through!

What Is Area Model Division (4th Grade)?

You can start your lesson by explaining that the area model division is simply a model that looks like a rectangular diagram that we use in mathematics to divide numbers.

More specifically, by applying this model, we break the rectangle into smaller boxes with the help of number bonds to make the division easier. In the end, to find out what the quotient is, we’ll simply add up the smaller boxes.

How to Teach Area Model Division (4th Grade)

Review place value.

Students need to have a solid understanding of place value to be able to use the area model for division. So make sure to review their place value understanding and identify any students that are still struggling with it.

You can introduce a brief activity by asking students to find the place value of each digit in a given number, such as finding the place value of 2, 3, 5, and 9 in 2,359. You may also want to check out our article on place value.

How to Perform Area Model Division (4th Grade)

After the brief review of place value concepts, you can proceed with teaching the steps of doing area model division to fourth graders. Start by saying that you want to find the quotient or the answer to a particular division problem, such as:

268 ÷ 2 = ?

You can explain to students that using the area model to solve this division problem requires drawing a rectangular area. Point out that we’ll divide the rectangular area into smaller parts and break up the dividend based on its place values. We’ll also keep the divisor at the very beginning to the left.

Since we know that 268 = 200 + 60 + 8, we can present it in the following way in the rectangle:

Explain that we’re doing this so that we end up with smaller areas that are easier to divide by two. That is, it’s easier to do the mental math of dividing 200 by 2 or 8 by 2 than dividing 268 by two.

Next, perform the division of each of these numbers by two:

200 ÷ 2 = 100

60 ÷ 2 = 30

Finally, point out that the only thing left to do is simply add up all of these partial quotients so as to get the quotient of 268 2. In other words:

100 + 30 + 4 = 134

By applying these simple steps of breaking up the dividend, we found out that 268 ÷ 2 = 134.

Why We Don’t Always Break Up Dividends This Much…

Make sure to point out to students that the way we break up a dividend varies from case to case. Highlight that the general rule to remember is that we try to break it up to pieces that would be easy to divide by the divisor.

Provide an example of this. For instance, let’s say we want to find the quotient of 972 ÷ 9. Ask students if it would be wise to break 972 into 900 + 70 + 2? If the students get the gist of the main principle of how the area model works, they should be able to reply ‘no’.

Why? Because while 900 may not be difficult to divide by the divisor, 70 is not easily divided by 9. So we’ll try to look for a number that we can easily divide by 9, which in this case is 72, as most students already know that 9 x 8 = 72 by heart.

Point out to students that this is why we’ll break up the dividend in the following way (again keeping the divisor at the beginning):

Explain that afterward, we’ll simply perform the steps we already implemented above, that is, we’ll divide each of these numbers by the divisor and add up the partial quotients in order to get the final quotient. In other words:

900 ÷ 9 = 100

100 + 8 = 108

So the quotient of 972 ÷ 9 is 108. Since students are already fluent in multiplication from previous lessons, you can encourage them to even check whether the answer is correct by multiplying 108 by 9.

Solving Word Problems With Area Model

Once children are comfortable with using the area model to solve division problems, you can introduce word problems that require division where the area model can also be applied. First, remind students that we need to identify the key question that is being asked in the problem.

It’s crucial to identify what information is important in the word problem and what isn’t. To do this, you can also encourage students to use a highlighter. Normally, this is something that students are familiar with from lessons on multiplication word problems.

You may also benefit from checking out our article on multiplication word problems.

You can then present a word problem requiring division to your class. For instance, take the following word problem:

“Ms. James bought 315 stickers for her classroom. She wants to give them out equally amongst her 5 students . How many stickers will each of them get?”

Point out that the main question that we’re trying to find out is the number of stickers students will get if Ms. James divides 315 stickers into 5 equal groups of stickers. By highlighting the number of stickers that Ms.James bought and the way she divided them to her 5 students we get an idea of what information we already have.

Thus, we can create the following equation:

315 ÷ 5 = ?

Now you can move on to using the area model to show students how to solve the division problem. Point out that we know that 15 is divisible by 5 and 300 is divisible by 5 as well (since we know that 30 can be divided by 5). So we can break up the dividend as follows:

300 ÷ 5 = 60

Then, we’ll simply add the partial quotients:

60 + 3 = 63

So the final quotient is 63.

Activities to Practice Area Model Division

This is a simple activity that will help children reinforce their knowledge of area model division. To implement this activity, you’ll need to bring large construction paper and division cards (i.e. cards with division problems) in class. You’ll also need a number of markers.

Divide students into pairs. Make sure that students are adequately paired up so that those that have stronger math skills are paired with students whose math skills may not be so strong. Provide students with the instructions for the activity.

Each pair gets one division card, construction paper, and markers. Explain to your students that they’re supposed to work together with their partners to present and solve the division problem on the construction paper with markers, using the area model.

For example, if students got a division card with the following division problem: 455 ÷ 5, they’re supposed to create an area model on the construction paper, and break the dividend based on its place values in order to find the quotient.

At the end of the activity, each pair presents their construction paper in front of the class. Encourage students to actively explain each step of the way and why they solved the division problem the way they did.

Area Model Division Task Cards

This is a fun game that you can use in your class to practice division using area models. To play this game, you’ll need to prepare task cards with division word problems on them. Make sure you have one word problem per group, depending on the number of students.

Divide students into groups of 3, 4. Hand out one task card to each group. Explain that they have to work together with the other members of the group in order to solve the word problem. Point out that they must use the are model to solve the problem.

The first group that manages to solve the problem on their task card wins the game. In case of a tie, you can also introduce two additional task cards to the given groups. The first one that manages to solve the word problem is declared the winner.

Before You Leave…

If you enjoyed these tips and information, we have a whole lesson on teaching area model division to 4th graders! So if you need guidance to structure your class and teach it, sign up for our emails for more free lessons and content!

Feel free to also check out our blog – you’ll find plenty of awesome resources that you can use in your class! And if you’re ready to become a member, simply sign up at Math Teacher Coach !

This article is based on:

Unit 4 – Multi-Digit Whole Number Division

4-1 Division Using Area Models
4-2 Whole Number Quotients and Remainders
4-3 Factors and Multiples
4-4 Prime and Composite Numbers
4-5 Division of Multiples of 10, 100, and 1,000 by Single-Digit Numbers
4-6 Three and Four-Digit Division with Divisors of 2, 3, 4, and 5
4-7 Division with a Zero in the Dividend or in the Quotient
4-8 Division with Divisors of 6, 7, 8, and 9
4-9 Solve One-Step Word Problems

Division using Models

Embedded in this unit of printable division worksheets are varied strategies for 3rd grade, 4th grade, and 5th grade kids to learn the basics of division with a range of hands-on tasks, such as cut-and-paste sharing activity, drawing objects for equal sharing, division by grouping objects, dividing by distributing objects in rows and columns of the array model, number line, bar model and area model. Gain a free access to some of these tasks.

» Division by Grouping Models

» Division Array Models

» Division using a Number Line

Division by Sharing | Cut-and-Paste Activity

Spin a story around the illustrations to introduce the concept of division. Snip the pictures, divide them into two equal parts and glue them in the columns and learn division by equal sharing in the process.

Download the set

Division by Sharing | Drawing Activity

Blend fun and learning with this alternative pdf exercise for grade 3 kids. Read the scenario carefully, share the objects evenly, draw the correct number of specified objects in each group to complete the worksheets.

Pictorial models to divide numbers is an interesting strategy and most helpful in solving word problems. Represent the division equation as a rectangular bar and divide the bar into equal parts to find the quotient.

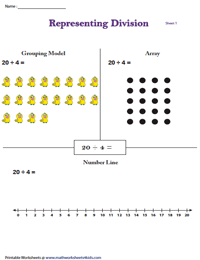
Representing Division in 3 Models | Activity

Recapitulate three division methods with this set of interesting 3-in-1 activity worksheet pdfs. Solve for the quotient by representing each division equation as a grouping model, an array model and on a number line.

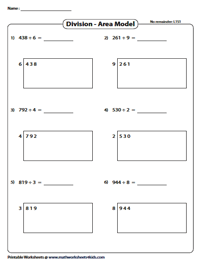
Area Models Worksheets | Without Remainder – Level 1

Visually represent the division equation as a rectangle with these level 1 area models. Figure out the quotient by dividing the given 3-digit numbers inside the rectangle by the single-digit divisors. Repeat the process until you get a 0.

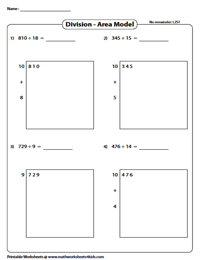
Area Models Worksheets | Without Remainder – Level 2

With double-digit divisors in place, these printable area models worksheets help 4th grade kids relate divisor and quotient to the width and length of the rectangle and the dividend to the area of the rectangle. Go on dividing!

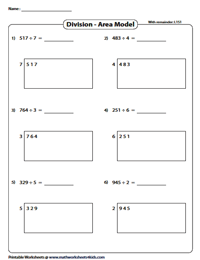
Area Models Worksheets | With Remainder – Level 1

Direct students of grade 4 and grade 5 to solve the division equation using the area or box method by repeatedly subtracting the multiples until they can't be subtracted anymore and add up the partial quotients and find the remainder.

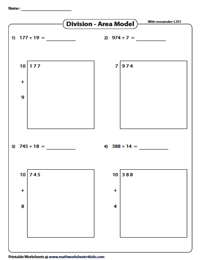
Area Models Worksheets | With Remainder – Level 2

These level 2 area models pdf worksheets present the area and the width of a rectangle and help kids identify the length by performing division. They continue dividing the area by width until they get a remainder < divisor and write down the quotient obtained as the length.

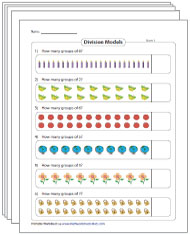
Division by Grouping Model Worksheets

Familiarize 3rd grade kids with the grouping strategy of division using this set of printable worksheets. Group objects, answer questions based on the model, complete the division statements, figure out left overs and much more.

(27 Worksheets)

Division Array Model Worksheets

Work out the quotient by observing arrays of objects distributed across rows and columns, answer questions, decipher arrays to write a division sentence, solve word problems and draw arrays to bolster division skills.

(16 Worksheets)

Division using a Number Line Worksheets

Interpret the division sentences on the number lines by drawing hops, read the number line and write the division equation, MCQs and many such activities, help develop division skills with ease.

(40 Worksheets)

Related Worksheets

» Division Tables and Charts

» Divisibility Rules

» Basic Division

» In and Out Boxes for Division

» Multiplication and Division Fact Family

Become a Member

Membership Information

What's New?

Printing Help

Testimonial

This is a members-only feature!

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 3: Multiplication and division

About this unit.

In this topic, we will multiply and divide whole numbers. The topic starts with 1-digit multiplication and division and goes through multi-digit problems. We will cover regrouping, remainders, and word problems.

Multiplication intro

Multiplication as equal groups (Opens a modal)
Intro to multiplication (Opens a modal)
Basic multiplication (Opens a modal)
Multiplication with arrays (Opens a modal)
Worked example: Whole numbers on the number line (Opens a modal)
More ways to multiply (Opens a modal)
Ways to represent multiplication (Opens a modal)
Understand multiplication using groups of objects 7 questions Practice
Multiply with arrays 7 questions Practice
Represent multiplication on the number line 4 questions Practice

Multiplication facts

Multiplication tables for 2-9 (Opens a modal)
Multiplication tables for 10, 11, 12 (Opens a modal)
Multiply by 0 or 1 14 questions Practice
Multiply by 2 7 questions Practice
Multiply by 3 7 questions Practice
Multiply by 4 7 questions Practice
Multiply by 5 7 questions Practice
Multiply by 6 7 questions Practice
Multiply by 7 14 questions Practice
Multiply by 8 14 questions Practice
Multiply by 9 14 questions Practice
Basic multiplication 7 questions Practice

Properties of multiplication

Properties of multiplication (Opens a modal)
Properties and patterns for multiplication (Opens a modal)
Associative property of multiplication (Opens a modal)
Commutative property of multiplication review (Opens a modal)
Associative property of multiplication review (Opens a modal)
Distributive property review (Opens a modal)
Commutative property of multiplication 7 questions Practice
Associative property of multiplication 7 questions Practice
Distributive property 4 questions Practice

Multiplying by tens

Multiplying by multiples of 10 (Opens a modal)
Multiplying by tens word problem (Opens a modal)
Multiply by tens 7 questions Practice
Multiply by tens word problems 4 questions Practice

Multiplication by 10s, 100s, and 1000s

Multiplying 10s (Opens a modal)
Multiplying 1-digit numbers by multiples of 10, 100, and 1000 (Opens a modal)
Multiplying 1-digit numbers by 10, 100, and 1000 (Opens a modal)
Multiplying 10s 7 questions Practice
Multiply 1-digit numbers by a multiple of 10, 100, and 1000 7 questions Practice
Multiply 1-digit numbers by 10, 100, and 1000 7 questions Practice

Multiplication: place value and area models

Using area model and properties to multiply (Opens a modal)
Multiplying with distributive property (Opens a modal)
Multiplying with area model: 6 x 7981 (Opens a modal)
Multiplying with area model: 78 x 65 (Opens a modal)
Lattice multiplication (Opens a modal)
Why lattice multiplication works (Opens a modal)
Multiply 2-digits by 1-digit with distributive property 4 questions Practice
Multiply 2-digit numbers with area models 4 questions Practice

Multi-digit multiplication

Multiplying 2-digit by 1-digit (Opens a modal)
Multiplying 3-digit by 1-digit (Opens a modal)
Multiplying 3-digit by 1-digit (regrouping) (Opens a modal)
Multiplying 4-digit by 1-digit (regrouping) (Opens a modal)
Multiplying 2-digit numbers (Opens a modal)
Multiplying 2-digit by 2-digit: 36x23 (Opens a modal)
Multiplying 2-digit by 2-digit: 23x44 (Opens a modal)
Multiplying multi-digit numbers (Opens a modal)
Multiply without regrouping 7 questions Practice
Multiply with regrouping 7 questions Practice
Multiply 2-digit numbers 7 questions Practice
Multi-digit multiplication 4 questions Practice

Relating multiplication and division

Relating division to multiplication (Opens a modal)
Multiplication word problem: parking lot (Opens a modal)
Division word problem: school building (Opens a modal)
Relate division to multiplication 7 questions Practice
Relate division to multiplication word problems 4 questions Practice

Division intro

The idea of division (Opens a modal)
Intro to division (Opens a modal)
Ways to represent division (Opens a modal)
Division with groups of objects 7 questions Practice
Divide with visuals 7 questions Practice

Division facts

No videos or articles available in this lesson
Divide by 1 11 questions Practice
Divide by 2 10 questions Practice
Divide by 3 10 questions Practice
Divide by 4 10 questions Practice
Divide by 5 10 questions Practice
Divide by 6 10 questions Practice
Divide by 7 10 questions Practice
Divide by 8 10 questions Practice
Divide by 9 10 questions Practice
Divide by 10 10 questions Practice
Basic division 7 questions Practice

Division problems that work out nicely

Quotients that are multiples of 10 (Opens a modal)
Canceling zeros when dividing (Opens a modal)
Divide multiples of 10, 100, and 1,000 by 1-digit numbers 7 questions Practice
Cancel zeros when dividing 7 questions Practice

Division: place value and area

Division using place value (Opens a modal)
Division with area models (Opens a modal)
Divide using place value 4 questions Practice
Divide by 1-digit numbers with area models 4 questions Practice

Multi-digit division (no remainders)

Intro to long division (no remainders) (Opens a modal)
Long division: 280÷5 (Opens a modal)
Divide multi-digit numbers by 2, 3, 4, and 5 (remainders) 7 questions Practice
Zeros in the dividend (no remainders) 4 questions Practice
Zeros in the quotient (no remainders) 4 questions Practice
Intro to remainders (Opens a modal)
Understanding remainders (Opens a modal)
Interpreting remainders (Opens a modal)
Long division with remainders: 3771÷8 (Opens a modal)
Long division with remainders: 2292÷4 (Opens a modal)
Divide with remainders (2-digit by 1-digit) 4 questions Practice
Divide multi-digit numbers by 6, 7, 8, and 9 (remainders) 4 questions Practice
Multi-digit division 4 questions Practice

Multi-digit division (remainders)

Intro to long division (remainders) (Opens a modal)
Dividing by 2-digits: 6250÷25 (Opens a modal)
Dividing by 2-digits: 9815÷65 (Opens a modal)
Dividing by 2-digits: 7182÷42 (Opens a modal)
Partial quotient method of division: introduction (Opens a modal)
Partial quotient method of division: example using very large numbers (Opens a modal)
Divide by taking out factors of 10 4 questions Practice
Basic multi-digit division 7 questions Practice
Division by 2-digits 4 questions Practice

Multiplication and division word problems

Multiplication word problem: carrots (Opens a modal)
Division word problem: row boat (Opens a modal)
Multiplication word problem: pizza (Opens a modal)
Division word problem: field goals (Opens a modal)
Multiplication, division word problem: pedaling (Opens a modal)
Multiplication and division word problems 7 questions Practice
Multi-step word problems with whole numbers 4 questions Practice

1st Grade Math
2nd Grade Math
3rd Grade Math
4th Grade Math
5th Grade Math
6th Grade Math
7th Grade Math
8th Grade Math
Knowledge Base
Math for kids

Area Model Division – Definition, Examples, Facts

Created on Dec 24, 2023

Updated on January 5, 2024

Welcome to another informative and engaging post from the Brighterly series aimed at making math enjoyable and understandable for children! Today, we’re diving into a fascinating concept – the Area Model Division. This topic is much more than just numbers; it represents a unique perspective on division that helps children visualize and grasp the concept in an exciting and engaging way.

Area Model Division, a visual teaching approach that emphasizes the understanding of area, is a far cry from the routine algorithmic methods. Instead of following mechanical processes, children get to see how division plays out in an appealing visual form. Picture a rectangle representing the total amount being divided. This rectangle is then broken into smaller, equally-sized sections, each depicting the divisor. Quite different from your usual division lesson, right?

What is Area Model Division?

Area model division is a visual method of teaching division that emphasizes the concept of area. Unlike the standard algorithmic division methods, which can be mechanical and abstract, the area model provides a concrete, spatial perspective on division. Using an area model to demonstrate division allows learners to fully understand the concept of division rather than just perform repetitive calculations. This innovative approach engages learners in a visual, interactive, and creative way that not only keeps them interested but also encourages them to think critically and logically.

This teaching strategy is part of the larger Common Core standards designed to boost students’ understanding of mathematical concepts. The area model is frequently used in elementary classrooms, but its simplicity and effectiveness make it a valuable tool for all ages. It has revolutionized the way division is taught, providing a more inclusive, effective, and engaging learning experience.

Definition of Area Model Division

Area model division is a pedagogical strategy that defines division in terms of the division of an area into equal parts. Imagine a rectangular region representing the total value being divided. This area is then subdivided into smaller, equally-sized rectangular areas, each representing the divisor. The quotient is then the number of these smaller rectangles that fit within the original larger rectangle.

This method of teaching division is part of the visual mathematics approach that helps children understand abstract concepts by visualizing them as shapes and diagrams. This approach improves mathematical comprehension, problem-solving skills, and logical reasoning abilities.

How Does Area Model Division Work?

The area model division operates by visually depicting division problems. For example, if we are dividing 18 by 3, we envision an area (rectangle) of 18 units. This area is then divided into smaller sections or “sub-areas,” each representing a value of 3. The number of these sub-areas equates to the quotient of our division.

Here, the divisor is the size of the sub-areas, the dividend is the total area, and the quotient is the number of sub-areas. By breaking down a larger area into smaller sections, learners gain a concrete understanding of what division entails. The area model thus provides a vivid illustration of the mathematical principle of division and is a practical tool in learning and teaching mathematics.

Benefits and Uses of Area Model Division

The area model division is lauded for numerous benefits, especially its utility in improving the understanding of division. It encourages spatial thinking, enhances problem-solving abilities, and promotes a deeper comprehension of mathematical concepts. This model is especially beneficial for visual learners, but it is advantageous for all types of learners due to its interactive nature.

The area model division can be used to simplify complex division problems, teach the concepts of fractions and ratios, and lay the foundation for more advanced mathematical concepts such as algebra and geometry. It is a vital tool in mathematics education that bridges the gap between abstract concepts and real-world applications.

Examples of Area Model Division

Here are a few examples of area model division:

Dividing 20 by 4 would entail drawing a rectangle with an area of 20 units and then dividing this rectangle into four equal rectangles, each with an area of 5 units.

To divide 36 by 6, we’d illustrate a rectangle of 36 units, then subdivide it into six smaller rectangles of 6 units each.

These examples illustrate how area model division translates numerical division problems into visual tasks, making the process of division more tangible and accessible to learners.

Steps in Area Model Division

Here are the steps involved in using area model division:

Determine the dividend and the divisor.
Draw a rectangle to represent the total area (the dividend).
Divide this rectangle into smaller rectangles, each with an area equal to the divisor.
Count the number of smaller rectangles to find the quotient.

These steps are repeated for different division problems, providing a consistent method for teaching and understanding division.

Properties and Characteristics of Area Model Division

The area model division has some specific properties and characteristics:

It is visual and spatial, making abstract division concrete.
It promotes understanding over rote memorization.
It encourages logical reasoning and problem-solving skills.
It is interactive and engaging, keeping learners interested.
It is flexible and can be used for different division problems.

These properties make the area model division an effective teaching and learning tool in mathematics.

Comparing Area Model Division with Other Division Models

While traditional division methods focus on the algorithmic process, the area model division focuses on understanding the underlying concept. Other models, like long division or chunking, might be quicker for simple calculations, but they often lack the visual component that helps learners grasp the real meaning of division. In comparison, the area model division provides a visual representation, making it easier for students to understand the process of division. The concrete nature of the area model makes it particularly effective for teaching the concepts of division, especially to young learners.

Applying the Area Model Division in Real Life Context

The area model division has numerous real-life applications. It can be used in solving problems related to measurement, ratios, and fractions. For example, if a garden plot is divided into equal sections for different types of plants, the area model can visually demonstrate how the garden is divided. Similarly, if a pizza is divided into equal slices, the area model can illustrate the division of the pizza.

Equations and Formulas in Area Model Division

The area model division can be expressed using the equation Dividend = Divisor x Quotient . Here, the dividend is the total area, the divisor is the area of each sub-region, and the quotient is the number of such sub-regions. This equation illustrates the mathematical relationship underlying division and provides a simple way of representing division problems.

Deriving Equations using Area Model Division

The area model division is a powerful tool in deriving equations. For instance, the equation for the area of a rectangle ( Area = length x width ) can be applied in the area model of division. If we know the total area (the dividend) and the length (the divisor), we can find the width (the quotient) by using the area model division.

Practice Problems on Area Model Division

Here are a few practice problems:

Divide 24 by 4 using area model division.
Use the area model division to divide 30 by 5.
Solve 42 divided by 7 using area model division.

These practice problems can help learners apply the area model division in various scenarios, enhancing their understanding and proficiency in division.

At Brighterly, we believe that math can be fun and engaging, and the area model division is a shining example of that philosophy. Through visual illustrations and interactive activities, we aim to provide a solid foundation in mathematics for children while sparking their interest in the subject. The area model division has proven to be a dynamic teaching and learning tool that not only explains the concept of division but also inspires creativity and critical thinking.

The concept of dividing an area into equal parts provides an intuitive understanding of division and builds a robust base for advanced mathematical ideas. It’s our hope that this deep dive into the world of area model division has sparked curiosity, stimulated learning, and above all, made math a bit more fun. Stay tuned for more exciting math concepts with Brighterly!

Frequently Asked Questions on Area Model Division

What is area model division.

The area model division is a visual technique for teaching and learning division. Instead of focusing on mechanical calculations, this method illustrates the division process using the concept of an area. Imagine a rectangle – this represents the total value being divided, or the dividend. This rectangle is then divided into smaller, equal parts, each representing the divisor. The resulting number of these smaller parts gives the quotient. The area model division encourages understanding the concept behind the division process, rather than just performing the calculation.

How does area model division work?

Area model division works by visually representing division problems using areas. Let’s say we’re dividing 15 by 3. We begin by imagining an area (rectangle) of 15 units. This area is then partitioned into smaller sections or “sub-areas,” each holding a value of 3. The number of these smaller parts or sub-areas gives us the quotient of our division. In other words, the total area (dividend) is split into smaller areas (divisor), and the quotient is how many of these smaller areas fit into the total area.

What are the benefits of area model division?

Area model division offers numerous benefits. It promotes spatial thinking and problem-solving abilities as students must visualize the division process. This method encourages learners to think about division in a different way, helping them to understand the underlying concept behind the mathematical operation. Also, area model division caters to different learning styles, particularly visual learners, and makes mathematics more interactive and engaging. It provides a robust foundation for more advanced mathematical concepts such as fractions, ratios, and algebra.

What are some examples of area model division?

Examples of area model division can vary widely depending on the numbers involved. For instance, when dividing 24 by 6, you can imagine a rectangle with an area of 24 units. This rectangle is then divided into six smaller rectangles, each with an area of 4 units. The six smaller rectangles are the result of the division. Similarly, to divide 35 by 7, you’d represent a rectangle of 35 units, then subdivide it into seven smaller rectangles of 5 units each. These examples show how the area model division can visualize and simplify the process of division.

What are the steps in area model division?

There are four main steps in the area model division. First, identify the dividend (the total area) and the divisor (the size of each sub-area). Then, draw a rectangle to represent the total area (the dividend). Next, divide this rectangle into smaller rectangles, each representing the divisor. Finally, count the number of these smaller rectangles to determine the quotient. This method provides a visual aid for understanding division and can be used repeatedly to solve a variety of division problems.

Education.gov
Wikipedia – Visual Mathematics
PubMed – Mathematics Education

I am a seasoned math tutor with over seven years of experience in the field. Holding a Master’s Degree in Education, I take great joy in nurturing young math enthusiasts, regardless of their age, grade, and skill level. Beyond teaching, I am passionate about spending time with my family, reading, and watching movies. My background also includes knowledge in child psychology, which aids in delivering personalized and effective teaching strategies.

Book 1 to 1 Math Lesson

Kid’s grade

After-School Math Program Boost Your Child's Math Abilities! Ideal for 1st-12th Graders, Perfectly Synced with School Curriculum!

$After-School Math Program$

After-School Math Program

Related math, 4800 in words.

The number 4800 is spelled as “four thousand eight hundred”. It is eight hundred more than four thousand. For example, if you have four thousand eight hundred coins, you have four thousand coins and then eight hundred extra coins, making four thousand eight hundred. Thousands Hundreds Tens Ones 4 8 0 0 How to Write […]

What is a Centimeter – Definition With Examples

Welcome to another exciting adventure in learning with Brighterly! Today, we’re diving into the world of measurements, and more specifically, we’re exploring the centimeter. A centimeter is more than just a unit of length; it’s a bridge that connects us to the world around us, making sense of spaces, objects, and distances. Just like a […]

Synthetic Division – Method, Definition With Examples

Every child embarks on a mathematical journey, and as they ascend the ladder, they encounter various techniques and methods. Here at Brighterly, we believe in illuminating these methods in the most engaging manner. Synthetic division is one such enchanting technique in polynomial arithmetic. This method, akin to a magical shortcut, allows young learners to swiftly […]

We use cookies to help give you the best service possible. If you continue to use the website we will understand that you consent to the Terms and Conditions. These cookies are safe and secure. We will not share your history logs with third parties. Learn More

Division Worksheets

Welcome to the division worksheets page at Math-Drills.com! Please give us your undivided attention while we introduce this page. Our worksheets for division help you to teach students the very important concept of division. If students have a good recall of multiplication facts, the division facts should be a breeze to teach. If you want your students to experience success in learning division, please make sure they know their multiplication facts to 81, how to multiply by 0 and how to multiply by 10. If they don't know these things, learning division will take a lot longer.

On this page you will find many Division Worksheets including division facts and long division with and without remainders. We start off with some division facts which are just the multiplication facts expressed in a different way. The main difference is that you can't divide by 0 and get a real number. If you really want your students to impress, say at their dinner table when their parents ask them what they learned today, you can teach them that division by zero is undefined.

The rest of the page is devoted to long division which for some reason is disliked among some members of the population. Long division is most difficult when students don't know their multiplication facts, so make sure they know them first! Oh, we already said that. What about a long division algorithm... maybe the one you or your parents or your grandparents learned? We adamantly say, yes! The reason that you and your ancestors used it is because it is an efficient and beautiful algorithm that will allow you to solve some of the most difficult division problems that even base ten blocks couldn't touch. It works equally well for decimals and whole numbers. Long division really isn't that hard.

Most Popular Division Worksheets this Week

$3-Digit by 1-Digit Long Division with Remainders and Steps Shown on Answer Key$

Division Facts Tables

$problem solving model division$

Like their counterparts on the multiplication facts page, these division facts tables can be used in a variety of ways to help students learn division facts. Students can memorize, look for patterns in the tables, compare them to multiplication tables, write answers on the versions with the answers omitted, or a variety of other learning activities. The tables come in gray, color and Montessori color depending on what fits you and your printer or school the best. For those that have already mastered the facts up to 12, they might be challenged to try the 13 to 24 versions.

Division Facts Tables for Facts from 1 to 12 Division Facts Tables in Gray 1 to 12 Division Facts Tables in Gray 1 to 12 (Answers Omitted) Division Facts Tables in Color 1 to 12 Division Facts Tables in Color 1 to 12 (Answers Omitted) Division Facts Tables in Color 1 to 12 with Individual Facts Highlighted Division Facts Tables in Montessori Colors 1 to 12 Division Facts Tables in Montessori Colors 1 to 12 (Answers Omitted)
Division Facts Tables for Facts from 13 to 24 Division Facts Tables in Gray 13 to 24 Division Facts Tables in Gray 13 to 24 (Answers Omitted) Division Facts Tables in Color 13 to 24 Division Facts Tables in Color 13 to 24 (Answers Omitted)

Division Facts up to the 7 Times Table

$problem solving model division$

If your students aren't quite ready for all of the division facts at once, this might be a good place to start. Perhaps they are really good at the multiplying up to 5; there is a worksheet to help them practice, and when they are ready, they can include 6 then 7. This section includes vertical questions with the traditional division symbol (aka bracket) and some arranged with a division symbol like you might see addition, subtraction or multiplication arranged.

Division Facts up to the 7 Times Table with a Long Division Symbol Vertical Division Facts Up To The 5 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 6 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 7 Times Table With Long Division Symbol/Bracket (50 per page) ✎
Division Facts up to the 7 Times Table with a Division Sign Vertical Division Facts Dividends to 25 With Division Sign Vertical Division Facts Dividends to 36 With Division Sign Vertical Division Facts Dividends to 49 With Division Sign

More worksheets with division facts up to 7, but these ones are arranged horizontally. This is a more natural arrangement for students who are used to reading things from left to right, allows them to practice recalling the answers and it is possible to fit 100 of these questions on the page without it getting too cluttered. If clutter is a problem though, there are also 50 and 25 question options.

Horizontally Arranged Division Facts up to the 5 Times Table Horizontally Arranged Division Facts with Dividends to 25 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 25 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 25 ( 25 Questions ; Large Print) ✎
Horizontally Arranged Division Facts up to the 6 Times Table Horizontally Arranged Division Facts with Dividends to 36 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 36 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 36 ( 25 Questions ; Large Print) ✎
Horizontally Arranged Division Facts up to the 7 Times Table Horizontally Arranged Division Facts with Dividends to 49 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 49 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 49 ( 25 Questions ; Large Print) ✎

Some students require chunking and more practice before they can handle the more complex pages with many different divisors. Here the worksheets only contain one divisor and there are several repetitions of the set on each page.

Dividing by Individual Facts up to the 7 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 7 ( 50 Questions ) ✎
Dividing by Groups of Individual Facts up to the 7 Times Table Vertically Arranged Dividing by 1, 2 and 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 7 ( 50 Questions ) ✎

More individual division facts worksheets but with a horizontal arrangement. This section includes 50 and 25 question options with each set repeated on the page.

Horizontally Arranged Dividing by Individual Facts up to the 7 Times Table (50 Questions per Page) Horizontally Arranged Dividing by 1 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 7 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 7 ( 50 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts up to the 7 Times Table (25 Large Print Questions per Page) Horizontally Arranged Dividing by 1 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 7 ( 25 Questions ; Large Print) ✎

Division Facts up to the 9 Times Table

$problem solving model division$

Manipulatives can help students "get" the concept of division. For example, students could regroup base ten blocks into units, then divide the units into piles. For the question 81 ÷ 9, students would start with eight ten blocks and one unit block. They would trade in the ten blocks for unit blocks and try to distribute all 81 of the unit blocks into nine piles. If they did it correctly, they would end up with 9 piles of 9 units and could say that 81 ÷ 9 = 9 as there are 9 units in each pile.

Division Facts up to the 9 Times Table With a Long Division Symbol Vertical Division Facts Up To The 8 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 9 Times Table With Long Division Symbol/Bracket (50 per page) ✎
Division Facts up to the 9 Times Table with a Division Sign Vertical Division Facts Dividends to 64 With Division Sign Vertical Division Facts Dividends to 81 With Division Sign Large Print Vertical Division Facts Dividends to 81 With Division Sign

If students learn up to the 9 times table and can do all the related division, they are likely to do well in later math studies. Long multiplication and long division, algebra, and many other math topics rely on students knowing these facts. Division facts worksheets up to the nine times tables can be used for students to practice, as a diagnostic test to see what gaps exist, or as a mastery test before moving on to the next topic. This section includes horizontally arranged questions which allows for a 100 per page option. Worksheets up to the 8 times table are also included to ensure a continual flow with the rest of this page, say, if you were adding one number at a time.

Horizontally Arranged Division Facts up to the 8 Times Table Horizontally Arranged Division Facts with Dividends to 64 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 64 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 64 ( 25 Questions ; Large Print) ✎
Horizontally Arranged Division Facts up to the 9 Times Table Horizontally Arranged Division Facts with Dividends to 81 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 81 ( 50 Questions ) ✎ Horizontally Arranged Division Facts with Dividends to 81 ( 25 Questions ; Large Print) ✎

More individual facts where a single number is used as the divisor throughout the entire worksheet. The quotients end up being in the range 1 to 9. These are great for students that need more practice on one or more divisors. This might be identified using a diagnostic test of a worksheet that includes all the division facts. If students consistently get questions wrong with a certain divisor, these worksheets might help them.

Dividing by Individual Facts up to the 9 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 9 ( 50 Questions ) ✎
Dividing by Groups of Individual Facts up to the 9 Times Table Vertically Arranged Dividing by 1, 2 and 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 9 ( 50 Questions ) ✎

Same as the previous section except with horizontally arranged questions and more options for the number of questions per page.

Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 100 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 50 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts up to the 9 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 9 ( 25 Questions ; Large Print) ✎

Division Facts up to the 10 Times Table

$problem solving model division$

Ten is such an important number in math. Our entire numbering system is based on tens. There are ten digits and each lower place is a tenth (divided by 10) of the place before it. Although 10 is a two-digit number, it is almost always included in multiplication and division facts learning. Multiplying and dividing by 10 is so important there is a whole page (powers of ten) on Math-Drills dedicated to it.

If you jumped right to this section, you cannot be blamed! A lot of students learn their times tables all at once and that means including the most important 10! So, when they are ready for division worksheets, they are ready for this section. For students who might be struggling a bit though, please scroll up and start them off with something a little more at their pace.

Division Facts up to the 10 Times Table With a Long Division Symbol Vertical Division Facts Up To The 10 Times Table With Long Division Symbol/Bracket (50 per page) ✎
Division Facts up to the 10 Times Table with a Division Sign Vertical Division Facts Dividends to 100 With Division Sign

Even with its size, 10 is often the easiest divisor to use... well, besides 1. This section includes horizontally arranged practice questions for all the division facts from the 1 times to the 10 times table.

Horizontally Arranged Division Facts up to the 10 Times Table Horizontally Arranged Division Facts with Dividends to 100 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 100 ( 50 Questions ) ✎

The worksheets in this section are included for students that need the facts one at a time with quotients from 1 to 10.

Dividing by Individual Facts up to the 10 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 10 with Quotients 1 to 10 ( 50 Questions ) ✎
Dividing by Groups of Individual Facts up to the 10 Times Table Vertically Arranged Dividing by 1, 2, 5 and 10 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 10 ( 50 Questions ) ✎

A horizontal repeat of the previous section.

Horizontally Arranged Dividing by Individual Facts up to the 10 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 100 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts with up to the 10 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 50 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts up to the 10 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 10 ( 25 Questions ; Large Print) ✎

Division Facts up to the 12 Times Table

$problem solving model division$

Ah, twelve. Educators have a penchant for the the 12 times table likely because it is important in clocks, eggs, the Vendergood language, and definitely to the Dozenal Societies of America and Great Britain. In mathematics, it is seen mostly in the completion of both multiplication and division facts worksheets. Since Math-Drills is happy to support the base twelve system, we present worksheets with division facts up to the 12 times table in the unlikely event that the duodecimal (aka dozenal) system is ever adopted.

Division Facts up to the 12 Times Table with a Long Division Symbol Vertical Division Facts Up To The 11 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To The 12 Times Table With Long Division Symbol/Bracket (50 per page) ✎
Division Facts up to the 12 Times Table with a Division Sign Vertical Division Facts Dividends to 144 With Division Sign

Division is essentially asking the question, "How many _____'s are in _____?" For the question, 81 ÷ 9, the prompt would sound like, "How many 9's are in 81?" This prompt will benefit students in later math studies when there are more complex concepts such as dividing decimals or fractions. "How many thirds are in four?" or even better, "How many third cups are in four cups?" If necessary, get out the measuring cups.

This important section includes worksheets with division facts up to the 12 times table with a 100 question option.

Horizontally Arranged Division Facts up to the 12 Times Table Horizontally Arranged Division Facts with Dividends to 144 ( 100 Questions) ✎ Horizontally Arranged Division Facts with Dividends to 144 ( 50 Questions ) ✎

So, if you are having your students learn division facts up to the 12 times table, it might be useful to have some worksheets with individual facts for a few students who might be overwhelmed with everything at once!

Dividing by Individual Facts up to the 12 Times Table Vertically Arranged Dividing by 1 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 2 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 4 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 5 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 8 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 11 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 12 with Quotients 1 to 12 ( 50 Questions ) ✎
Dividing by Groups of Individual Facts up to the 12 Times Table Vertically Arranged Dividing by 1, 2, 5 and 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 3, 4 and 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 7, 8 and 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Vertically Arranged Dividing by 11 and 12 with Quotients 1 to 12 ( 50 Questions ) ✎

Same idea as the previous section, but with a horizontal arrangement and different numbers of questions on each page.

Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (100 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 100 Questions ) ✎
Horizontally Arranged Dividing by Groups of Individual Facts up to the 12 Times Table (100 Questions) Horizontally Arranged Dividing by 1, 2, 5 and 10 (Quotient 1-12)
Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (50 Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 50 Questions ) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 50 Questions ) ✎
Horizontally Arranged Dividing by Individual Facts up to the 12 Times Table (25 Large Print Questions) Horizontally Arranged Dividing by 1 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 2 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 3 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 4 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 5 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 6 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 7 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 8 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 9 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 10 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 11 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎ Horizontally Arranged Dividing by 12 with Quotients 1 to 12 ( 25 Questions ; Large Print) ✎

Division Facts beyond the 12 Times Table

$problem solving model division$

Scenario: you have some students that have aced the division facts up to the 12 times table and need more of a challenge. This section has got you covered. Is there an argument for learning division facts for times tables beyond 9? 10? 12? Sure, why not. Students are likely to apply their knowledge in future math studies by instantly recognizing that the square root of 625 is 25, for example.

Division Facts up to the 25 Times Table With a Long Division Symbol Vertical Division Facts Up To the 13 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 14 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 15 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 16 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 17 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 18 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 19 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts Up To the 20 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 21 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 22 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 23 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 24 Times Table With Long Division Symbol/Bracket (50 per page) ✎ Vertical Division Facts From 5 Up To the 25 Times Table With Long Division Symbol/Bracket (50 per page) ✎
Division Facts Up to the 15 Times Table With a Division Sign Vertical Division Facts Dividends to 169 With Division Sign Vertical Division Facts Dividends to 196 With Division Sign Vertical Division Facts Dividends to 225 With Division Sign

There are certainly a few questions on these worksheets that will be useful knowledge later on. If your students are interested in learning them, anything to do with 16, 20, 24, and 25 will certainly be useful, and likely someone could come up with a reason for learning the others. Sixteen is used in the base 16 (aka hexadecimal system), so converting hexadecimal numbers to decimal numbers involves dividing (and multiplying by 16). Twenty is a great number that is divisible by six different numbers and in turn is a factor of some important numbers. Twenty is also a coin unit in many countries. Twenty-four hours is the length of a day, so if you wanted to know how many days were in 288 hours, you might want to know your 24 times table division facts. Twenty-five, well that is the value of a quarter, isn't it? You could also calculate how many seconds of PAL video you have by dividing the number of frames by 25!

Horizontally Arranged Division Facts up to the 20 Times Table Horizontally Arranged Division Facts Up to the 13 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 14 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 15 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 16 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 17 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 18 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 19 Times Table ( 100 Questions) ✎ Horizontally Arranged Division Facts Up to the 20 Times Table ( 100 Questions) ✎

If the previous two sections are a little tough to handle right out of the gates, perhaps start with these worksheets that only deal with one of the divisors at a time.

Dividing by Individual Facts up to the 25 Times Table Vertically Arranged Dividing by 13 with Quotients 1 to 13 ( 50 Questions ) ✎ Vertically Arranged Dividing by 14 with Quotients 1 to 14 ( 50 Questions ) ✎ Vertically Arranged Dividing by 15 with Quotients 1 to 15 ( 50 Questions ) ✎ Vertically Arranged Dividing by 16 with Quotients 1 to 16 ( 50 Questions ) ✎ Vertically Arranged Dividing by 17 with Quotients 1 to 17 ( 50 Questions ) ✎ Vertically Arranged Dividing by 18 with Quotients 1 to 18 ( 50 Questions ) ✎ Vertically Arranged Dividing by 19 with Quotients 1 to 19 ( 50 Questions ) ✎ Vertically Arranged Dividing by 20 with Quotients 1 to 20 ( 50 Questions ) ✎ Vertically Arranged Dividing by 21 with Quotients 1 to 21 ( 50 Questions ) ✎ Vertically Arranged Dividing by 22 with Quotients 1 to 22 ( 50 Questions ) ✎ Vertically Arranged Dividing by 23 with Quotients 1 to 23 ( 50 Questions ) ✎ Vertically Arranged Dividing by 24 with Quotients 1 to 24 ( 50 Questions ) ✎ Vertically Arranged Dividing by 25 with Quotients 1 to 25 ( 50 Questions ) ✎

Even more of the previous section, but with 100 questions per page and a horizonal arrangement.

Horizontally Arranged Dividing by Individual Facts up to the 25 Times Table Horizontally Arranged Dividing by 13 with Quotients 1 to 13 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 14 with Quotients 1 to 14 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 15 with Quotients 1 to 15 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 16 with Quotients 1 to 16 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 17 with Quotients 1 to 17 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 18 with Quotients 1 to 18 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 19 with Quotients 1 to 19 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 20 with Quotients 1 to 20 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 21 with Quotients 1 to 21 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 22 with Quotients 1 to 22 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 23 with Quotients 1 to 23 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 24 with Quotients 1 to 24 ( 100 Questions ) ✎ Horizontally Arranged Dividing by 25 with Quotients 1 to 25 ( 100 Questions ) ✎

Long division Worksheets

$problem solving model division$

Need an easier way to divide large numbers? Try this method using powers of ten. To successfully use this method, students need to be able to multiply by powers of ten and to subtract. Students subtract the dividend multiplied by decreasing powers of ten until they have zero or a remainder. Example: 1458 ÷ 54. Note 54 × 1 = 54, 54 × 10 = 540 (nothing greater is needed). 1458 - 540 - 540 = 378. Note that 540 was subtracted twice, so the number of times that 54 "goes into" 1458 so far is 20 times. Continuing, 378 - 54 - 54 - 54 - 54 - 54 - 54 - 54 = 0. Since 54 was subtracted seven times, the quotient increases by seven for a total of 27. In other words, 54 "goes into" 1458, 27 times.

We might also mention that this method can be even more sophisticated by using multiples of powers of ten. In the above example, using 54 × 5 = 270 would have helped to get to the quotient quicker.

Long Division Worksheets with No Remainders Long Division with No Remainders with a Multiple of Ten Divisor and a 2-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 1-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 2-Digit Quotient Long Division with No Remainders with a 1-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 2-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 2-Digit Divisor and a 4-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 3-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 4-Digit Quotient Long Division with No Remainders with a 3-Digit Divisor and a 5-Digit Quotient
European Format Long Division Worksheets with No Remainders European Format Long Division with No Remainders with a 1-Digit Divisor and a 1-Digit Quotient European Format Long Division with No Remainders with a 1-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 1-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 2-Digit Divisor and a 4-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 2-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 3-Digit Quotient European Format Long Division with No Remainders with a 3-Digit Divisor and a 4-Digit Quotient

Have you ever thought that you could help a student understand things better and get a more precise answer while still using remainders? It's quite easy really. Remainders are usually given out of context, including on the answer keys below. A remainder is really a numerator in a fractional quotient. For example 19 ÷ 3 is 6 with a remainder of 1 which is more precisely 6 1/3. Using fractional quotients means your students will always find the exact answer to all long division questions, and in many cases the answer will actually be more precise (e.g. compare 6 1/3 with 6.3333....).

Long Division Worksheets with Remainders Long Division with Remainders with a Multiple of Ten Divisor and a 2-Digit Quotient Long Division with Remainders with a 1-Digit Divisor and a 2-Digit Dividend Long Division with Remainders with a 1-Digit Divisor and a 3-Digit Dividend Long Division with Remainders with a 1-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 3-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 2-Digit Divisor and a 5-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 4-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 5-Digit Dividend Long Division with Remainders with a 3-Digit Divisor and a 6-Digit Dividend
European Format Long Division Worksheets with Remainders European Format Long Division with Remainders with a 1-Digit Divisor and a 2-Digit Dividend European Format Long Division with Remainders with a 1-Digit Divisor and a 3-Digit Dividend European Format Long Division with Remainders with a 1-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 3-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 2-Digit Divisor and a 5-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 4-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 5-Digit Dividend European Format Long Division with Remainders with a 3-Digit Divisor and a 6-Digit Dividend
Long Division Worksheets with Decimal Quotients Long Division with Decimal Quotients with a 1-Digit Divisor; 2-Digit Dividend Long Division with Decimal Quotients with a 1-Digit Divisor; 3-Digit Dividend Long Division with Decimal Quotients with a 1-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 3-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 2-Digit Divisor; 5-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 4-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 5-Digit Dividend Long Division with Decimal Quotients with a 3-Digit Divisor; 6-Digit Dividend
European Format Long Division Worksheets with Decimal Quotients European Format Long Division with Decimal Quotients with a 1-Digit Divisor; 2-Digit Dividend European Format Long Division with Decimal Quotients with a 1-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 2-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 2-Digit Divisor; 4-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 3-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 4-Digit Dividend European Format Long Division with Decimal Quotients with a 3-Digit Divisor; 5-Digit Dividend

We thought it might be helpful to include some long division worksheets with the steps shown. The answer keys for these division worksheets use the standard algorithm that you might learn if you went to an English speaking school. Learning this algorithm by itself is sometimes not enough as it may not lead to a good conceptual understanding. One tool that helps students learn the standard algorithm and develop an understanding of division is a set of base ten blocks. By teaching students division with base ten blocks first then progressing to the standard algorithm, students will gain a conceptual understanding plus have the use of an efficient algorithm for long division. Students who have both of these things will naturally experience more success in their future mathematical studies.

Long Division with 1-Digit Divisors with the Steps Shown on the Answer Key 2-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 3-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 4-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 1-Digit Long Division with Remainders with the Steps Shown on the Answer Key
Long Division with 2-Digit Divisors with the Steps Shown on the Answer Key 3-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 4-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 2-Digit Long Division with Remainders with the Steps Shown on the Answer Key
Long Division with 3-Digit Divisors with the Steps Shown on the Answer Key 4-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key 5-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key 6-Digit by 3-Digit Long Division with Remainders with the Steps Shown on the Answer Key

Some students find it difficult to get everything lined up when completing a long division algorithm, so these worksheets include a grid and wider spacing of the digits to help students get things in the right place. The answer keys include the typical steps that students would record while completing each problem; however, slight variations in implementation may occur. For example, some people don't bother with the subtraction signs,some might show steps subtracting zero, etc.

Long Division Worksheets with Grid Assistance and Prompts (No Remainders) 2-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 3-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and Prompts and NO Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and Prompts and NO Remainders
Long Division Worksheets with Grid Assistance Only (No Remainders) 3-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and NO Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and NO Remainders
Long Division Worksheets with Grid Assistance and Prompts (Some Remainders) 2-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 3-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and Prompts and some Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and Prompts and some Remainders
Long Division Worksheets with Grid Assistance Only (Some Remainders) 3-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 3-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 4-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 4-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 5-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 5-Digit by 2-Digit Long Division with Grid Assistance and some Remainders 6-Digit by 1-Digit Long Division with Grid Assistance and some Remainders 6-Digit by 2-Digit Long Division with Grid Assistance and some Remainders

Divisibility by 2, 5 and 10

A number is divisible by 2 if the final digit (the digit in the ones place) is even. Numbers ending in 0, 2, 4, 6, or 8 therefore are divisible by 2. A number is divisible by 5 if the final digit is a 0 or a 5. A number is divisible by 10 if the final digit is a 0.

Divisibility by 3, 6 and 9

A number is divisible by 3 if the sum of its digits is divisible by 3. For example, 285 is divisible by 3 because 2 + 8 + 5 = 15 is divisible by 3. A number is divisible by 6 if it is divisible by both 3 and 2 (see above rules). A number is divisible by 9 if the sum of its digits is divisible by 9. For examples, 285 is not divisible by 9 because 2 + 8 + 5 = 15 is not divisible by 9.

Divisibility by 4, 7 and 8

A number is divisible by 4 if the last two digits of the number are divisible by 4. For 7, there are a couple of strategies to use. Please see Divisibility Tricks for Learning Math for more information. A number is divisible by 8 if the last three digits are divisible by 8. This is the standard rule which can be a little sketchy for larger numbers, like who knows if 680 is divisible by 8? Because of this, we offer our Math-Drills.com solution which requires a little arithmetic, but can be accomplished quite easily with a little practice. As you know 8 is 2 to the third power, so we thought if you could divide the last three digits of a number by 2 three times, it would be divisible by 8. 680 ÷ 2 ÷ 2 ÷ 2 = 340 ÷ 2 ÷ 2 = 170 ÷ 2 = 85. We have a winner! 680 is indeed divisible by 8.

Divisibility Rules Worksheets with 2-Digit Numbers Divisibility of 2, 5 and 10 (2-digit) Divisibility of 3, 6 and 9 (2-digit) Divisibility of 4, 7 and 8 (2-digit) Divisibility of Numbers 2 to 10 (2-digit)
Divisibility Rules Worksheets with 3-Digit Numbers Divisibility of 2, 5 and 10 (3-digit) Divisibility of 3, 6 and 9 (3-digit) Divisibility of 4, 7 and 8 (3-digit) Divisibility of Numbers 2 to 10 (3-digit)
Divisibility Rules Worksheets with 4-Digit Numbers Divisibility of 2, 5 and 10 (4-digit) Divisibility of 3, 6 and 9 (4-digit) Divisibility of 4, 7 and 8 (4-digit) Divisibility of Numbers 2 to 10 (4-digit)

Dividing numbers in number systems other than decimal numbers including binary, quaternary, octal, duodecimal and hexadecimal numbers.

Worksheets for Long Division in Other Base Number Systems Dividing Binary Numbers (Base 2) Dividing Ternary Numbers (Base 3) Dividing Quaternary Numbers (Base 4) Dividing Quinary Numbers (Base 5) Dividing Senary Numbers (Base 6) Dividing Octal Numbers (Base 8) Dividing Duodecimal Numbers (Base 12) Dividing Hexadecimal Numbers (Base 16) Dividing Vigesimal Numbers (Base 20) Dividing Hexatrigesimal Numbers (Base 36) Dividing Various Numbers (Various Bases)

Book Lists by Age
Book Lists by Category
Reading Resources
Language & Speech
Raise a Reader Blog
Back to School
Success Guides by Grade
Homework Help
Social & Emotional Learning
Activities for Kids

Multiplication and Division Models and Strategies

Take a dive into the different strategies and models used in multiplication and division..

To build off my last blog about addition and subtraction , I would like to look at different strategies and models used in multiplication and division. It’s very important that students have an understanding of what they are doing — and not just memorize steps and procedures. They need to be able to analyze and think critically about numbers and how they are related. The traditional multiplication and division algorithms are important and every student does need to know how to use them, but not until after they have solidified their understanding. Starting with a concrete concept, moving to the pictorial and finally ending with the abstract will help students develop fully mastery.

Below are some models that students are using to help them understand the relationship between multiplication and division. Hopefully seeing these models and understanding how to use them will help you when you see your child using them.

Arrays: These are one of the earliest models used to help understand the concept of multiplication and division. They help students see the connection between the two operations, and students can visually see the “grouping” or “sharing” concept. Arrays are a great way to help students memorize their multiplication and division facts, instead of just using flash cards.

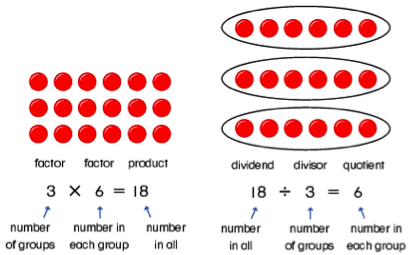
Image: Eduplace.org

Area Models: The area model is closely related to the computation used when computing with the standard algorithm. The difference is the visual representation and connection to the Base 10 System, and the understanding of place value. Students can visually see the actual size of each computation and learn how to interpret the partial products.

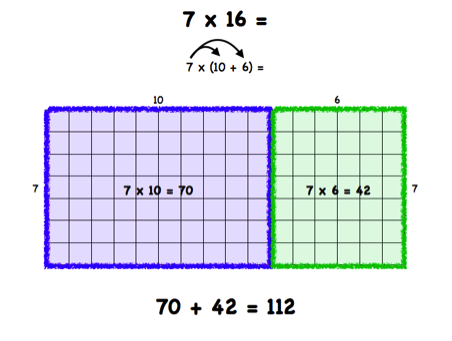
Image: Tes.com

Bar Models: Bar models are based on the concept of equal groups and part-part-wholes. This model helps students in moving away from the concrete phase and begins to help them understand the pictorial stage. Bar models are a great way to help students show their thinking when problem solving, especially when solving two-step problems.

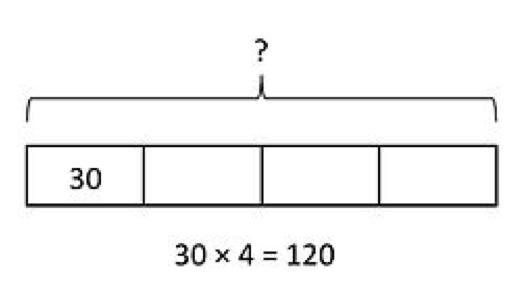
Image: Wikipedia.org

Number Lines: Number lines allow students to begin understanding the abstract stage of multiplication and division. Students begin to connect skip counting and multiples of a number to finding the product of a factor. They can “skip” forwards or backwards to represent the inverse operation. Number lines are great models to help students show their thinking and explain their reasoning.

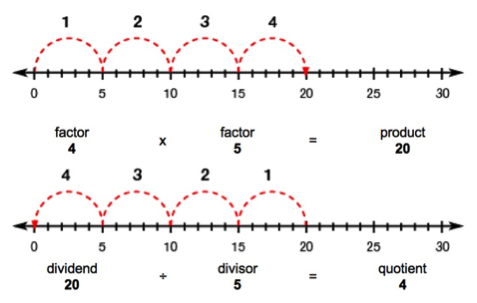
Image: Eduplace.com

Singapore math support and resources

Using Bar Models for Multiplication and Division

Do you know we can use bar models for multiplication and division problems? In this blog post, we illustrate some of the common types of word problems involving Multiplication and Division and how to solve them using this powerful heuristic.

Using Bar Models for Multiplication and Division in One-Step Multiplication Word Problems

Example (from Math in Focus workbook 3A):

School A collects 76 bundles of newspaper for recycling. School B collects 5 times the number of bundles as School A. How many bundles of newspaper does School B collect?

Bar model for one-step multiplication problem

Using Bar Models for Multiplication and Division in Two-Step Multiplication Word Problem

Jill has 28 stickers. Peggy has 4 times as many stickers as Jill. Luis has 15 fewer stickers than Peggy. How many stickers does Luis have?

Bar model for two-step multiplication problem

Using Bar Models for Multiplication and Division in One-Step Division Word Problem

Cally works 63 hours in 7 weeks. She works an equal number of hours per week. How many hours does she work per week?

Using Bar Models for Multiplication and Division in Two-Step Division Word Problem

Lance and Alex have 70 pencils. Lance has 4 times as many pencils as Alex. Alex’s pencils are shared equally among 2 children. How many pencils does each child get?

Related Resources

Video explanation and lesson plan (member’s resource).

https://teachablemath.com/lesson-plans/grade-3-lesson-plans/grade-3-semester-1-week-16-17/

Common Core Standards

D8 Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

Suggested Workbook Series

Math in Focus workbook (3A) Chapter 9 – Using Bar Models: Multiplication and Division (pages 159 to 180)
Primary Mathematics workbook (Common Core Edition) (3A) Chapter 3 – Multiplication and Division (pages 91 to 96)

For more related resources, please refer to our Bar Models page.

For more related resources, please refer to our Multiplication and Division page.

Word Problems on Division

Word problems on division for fourth grade students are solved here step by step.

Consider the following examples on word problems involving division: 1. $5,876 are distributed equally among 26 men. How much money will each person get? Solution: Money received by 26 men = 5876 So, money received by one man = 5876 ÷ 26 = 226

$Word Problem on Division$

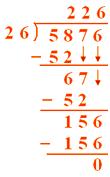
Each man will get $226.

2. If 9975 kg of wheat is packed in 95 bags, how much wheat will each bag contain?

Since 95 bags contain wheat 9975 kg Therefore, 1 bag contains wheat (9975 ÷ 95) kg = 105 kg

$Division Word Problem$

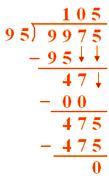
Each bag contains wheat = 105 kg In a problem sum involving division, we have to be careful about using the remainder.

3. 89 people have been invited to a banquet. The caterer is arranging tables. Each table can seat 12 people. How many tables are needed? Solution: To answer this question, we need to divide 89 by 12 89 ÷ 12

$Division Word Problems$

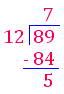
Quotient - 7

Remainder - 5

If the caterer arranges 7 tables, then 5 people will have no place to sit. So he needs to arrange 7 + 1 = 8 tables.

4. How many hours are there in 1200 minutes?

Solution: We know that there are 60 minutes in 1 hour.Divide the number of minutes by the number of minutes in 1 hour. We get, divide 1200 by 601200 ÷ 60 = 20

So there are 20 hours in 1200 minutes.

Answer: 20 hours.

5. A bus can hold 108 passengers. If there are 12 rows of seats on the bus, how many seats are in each row?

Solution: Total number of passengers = 108

There are 12 rows of seats on the bus.

To find how many seats are there in each row, divide the total number of passengers by the number of rows of seats on the bus.

We get, divide 108 by 12

108 ÷ 12 = 9

Therefore, there are 9 seats in each row.

Answer: 9 seats.

6. Tom had 63 apples. He divides all apples evenly among 9 friends. How many apples did Tom give to each of his friends?

Solution: Total number of apples = 63

There are 9 friends of seats on the bus.

To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends.

We get, divide 63 by 9

Therefore, Tom gives 7 apples to each of his friends.

Answer: 7 Apples

7. Mark baked 195 cookies and divided them equally into 13 packs. How many cookies did Mark put in each packet?

Solution: Total number of cookies = 195

There are 13 packs.

To find how many cookies did Mark put in each packet, divide the total number of cookies by the number of packs.

We get, divide 195 by 13

195 ÷ 13 = 15

Therefore, Mark put 15 cookies in each pack.

Answer: 15 cookies.

9. Nancy needs 5 lemons to make a glass of orange juice. If Nancy has 250 oranges, how many glasses of orange juice can she make?

Solution: Total number of oranges = 250

She needs 5 lemons to make a glass of orange juice.

To find how many glasses of orange juice can Nancy make, divide the total number of oranges by the number of oranges needed for each glass of orange juice.

We get, divide 250 by 5

250 ÷ 5 = 50

Therefore, Nancy can make 50 glasses of orange juice.

Answer: 50 glasses of orange juice.

10. In your classes you counted 120 hands. How many students were at the class?

Solution: Total number of hands = 120

We have 2 hands.

To find how many students were at the class, divide the total number of hands by the number of hands we have.

We get, divide 120 by 2

220 ÷ 2 = 60

Therefore, there were 60 students at the class.

Answer: 60 students.

11. The total train fare for 20 persons is 7540 rupees. What is the fare for 1 person.

12. A milk container can store 8 litres of milk. How many containers are required to stare 6,408 litres of milk?

Capacity of one container = 8 lites of milk

Required number of containers = 6408 ÷ 8

Hence, 801 containers are required.

$Word Problems on Division$

13. A farmer produced 29800 kg of wheat. How many bags will be buy store the wheat if one bag can hold 70 kg?

Produced = 29890 kg

Number of bags needed = 29899 ÷ 70

Therefore, 427 bags are needed to hold 29890 kg of wheat.

$Division Word Problem$

These are the basic word problems on division.

Questions and Answers on Word Problems on Division:

1. 92 bags of cement can be loaded in a truck. How many such trucks will be needed to load 2208 bags?

Answer: 24 trucks

2. The total train fare for 11 persons was $3850. What was the fare for one person?

Answer: $350

You might like these

$The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?$

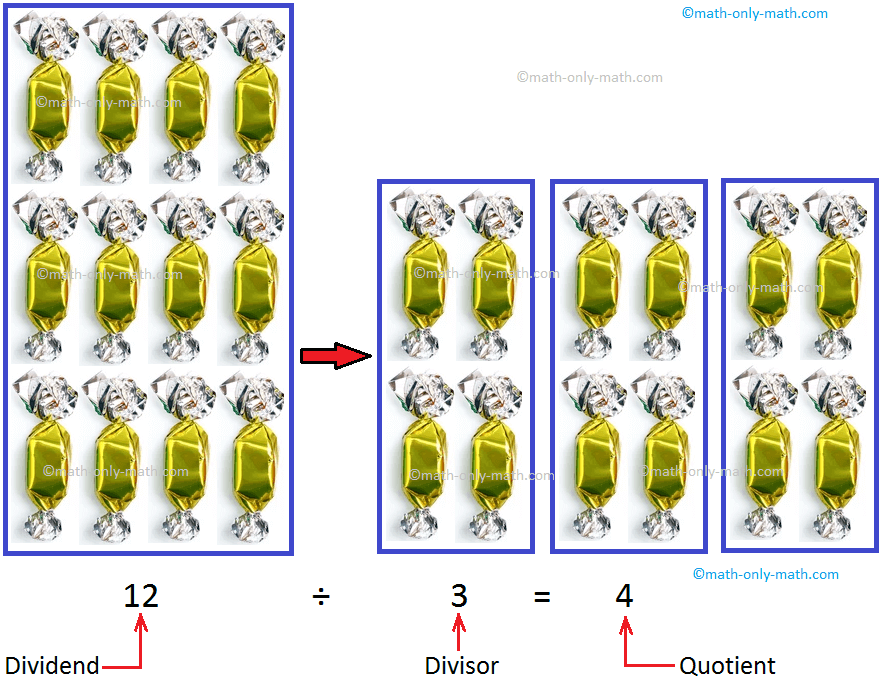
Terms Used in Division | Dividend | Divisor | Quotient | Remainder

The terms used in division are dividend, divisor, quotient and remainder. Division is repeated subtraction. For example: 24 ÷ 6 How many times would you subtract 6 from 24 to reach 0?

$The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also$

Successor and Predecessor | Successor of a Whole Number | Predecessor

The number that comes just before a number is called the predecessor. So, the predecessor of a given number is 1 less than the given number. Successor of a given number is 1 more than the given number. For example, 9,99,99,999 is predecessor of 10,00,00,000 or we can also

$In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:$

Worksheets on Comparison of Numbers | Find the Greatest Number

In worksheets on comparison of numbers students can practice the questions for fourth grade to compare numbers. This worksheet contains questions on numbers like to find the greatest number, arranging the numbers etc…. Find the greatest number:

$In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which$

Number Worksheets | Practice Different Questions on Numbers | Answers

In number worksheets, students can practice different questions on numbers from printable free worksheets for grade 4 math on numbers. Write the number which is 1 more than 9? Write the number which

$Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn$

Comparison of Numbers | Compare Numbers Rules | Examples of Comparison

Rule I: We know that a number with more digits is always greater than the number with less number of digits. Rule II: When the two numbers have the same number of digits, we start comparing the digits from left most place until we come across unequal digits. To learn

$In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,$

Formation of Numbers | Smallest and Greatest Number| Number Formation

In formation of numbers we will learn the numbers having different numbers of digits. We know that: (i) Greatest number of one digit = 9,

$In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.$

Formation of Numbers with the Given Digits |Making Numbers with Digits

In formation of numbers with the given digits we may say that a number is an arranged group of digits. Numbers may be formed with or without the repetition of digits.

$the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the$

Formation of Greatest and Smallest Numbers | Arranging the Numbers

the greatest number is formed by arranging the given digits in descending order and the smallest number by arranging them in ascending order. The position of the digit at the extreme left of a number increases its place value. So the greatest digit should be placed at the

$The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value$

Place Value | Place, Place Value and Face Value | Grouping the Digits

The place value of a digit in a number is the value it holds to be at the place in the number. We know about the place value and face value of a digit and we will learn about it in details. We know that the position of a digit in a number determines its corresponding value

$We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are$

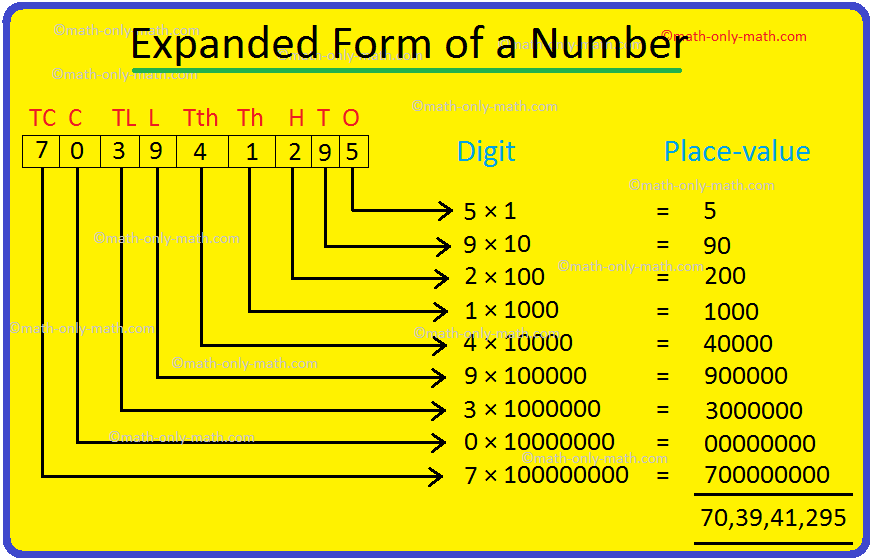
Expanded Form of a Number | Writing Numbers in Expanded Form | Values

We know that the number written as sum of the place-values of its digits is called the expanded form of a number. In expanded form of a number, the number is shown according to the place values of its digits. This is shown here: In 2385, the place values of the digits are

$Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371$

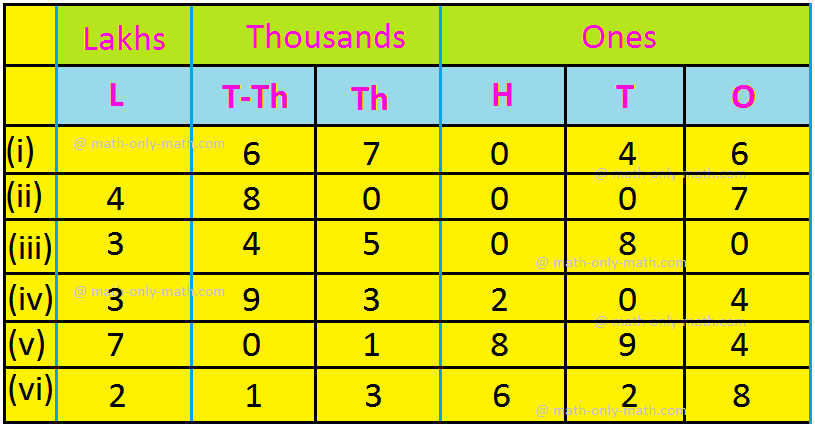
Worksheet on Place Value | Place Value of a Digit in a Number | Math

Worksheet on place value for fourth grade math questions to practice the place value of a digit in a number. 1. Find the place value of 7 in the following numbers: (i) 7531 (ii) 5731 (iii) 5371

$Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers$

Worksheet on Expanded form of a Number | Expanded Form of a Number

Worksheet on expanded form of a number for fourth grade math questions to practice the expanded form according to the place values of its digit. 1. Write the expanded form of the following numbers

$In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.$

Examples on the Formation of Greatest and the Smallest Number |Example

In examples on the formation of greatest and the smallest number we know that the procedure of arranging the numbers in ascending and descending order.

$In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students$

Worksheet on Formation of Numbers | Questions on Formation of Numbers

In worksheet on formation of numbers, four grade students can practice the questions on formation of numbers without the repetition of the given digits. This sheet can be practiced by students

$Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up$

Rounding off Numbers | Nearest Multiple of 10 | Nearest Whole Number

Rounding off numbers are discussed here, where we need to round a number. (i) If we purchase anything and its cost is $12 and 23¢, the cost is rounded up to it’s nearest $ 12 and 23¢ is left. (ii) If we purchase another thing and its cost is $15.78. The cost is rounded up

Related Concept

● Word Problems on Addition

● Subtraction

● Check for Subtraction and Addition

● Word Problems Involving Addition and Subtraction

● Estimating Sums and Differences

● Find the Missing Digits

● Multiplication

● Multiply a Number by a 2-Digit Number

● Multiplication of a Number by a 3-Digit Number

● Multiply a Number

● Estimating Products

● Word Problems on Multiplication

● Multiplication and Division

● Terms Used in Division

● Division of Two-Digit by a One-Digit Numbers

● Division of Four-Digit by a One-Digit Numbers

● Division by 10 and 100 and 1000

● Dividing Numbers

● Estimating the Quotient

● Division by Two-Digit Numbers

● Word Problems on Division

4th Grade Math Activities From Word Problems on Division to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

Preschool Activities
Kindergarten Math
1st Grade Math
2nd Grade Math
3rd Grade Math
4th Grade Math
5th Grade Math
6th Grade Math
7th Grade Math
8th Grade Math
9th Grade Math
10th Grade Math
11 & 12 Grade Math
Concepts of Sets
Probability
Boolean Algebra
Math Coloring Pages
Multiplication Table
Cool Maths Games
Math Flash Cards
Online Math Quiz
Math Puzzles
Binary System
Math Dictionary
Conversion Chart
Homework Sheets
Math Problem Ans
Free Math Answers
Printable Math Sheet
Funny Math Answers
Employment Test
Math Patterns
Link Partners
Privacy Policy

$XML RSS$

Recent Articles

$RSS$

Math Problem Answers | Solved Math Questions and Answers | Free Math

May 27, 24 06:47 PM

$Partial fraction$

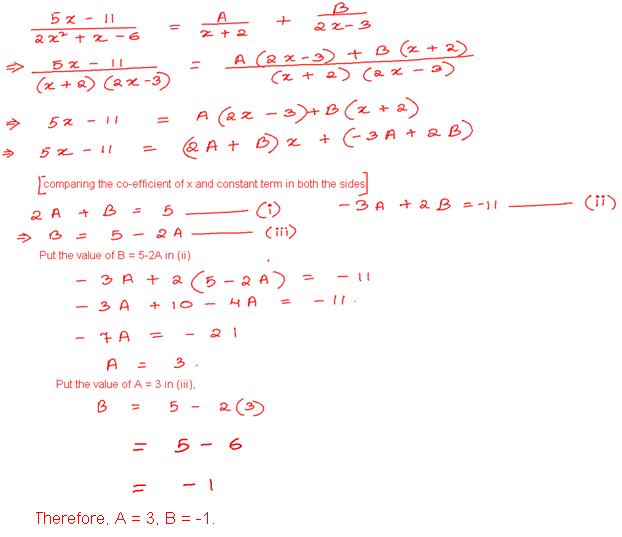
Properties of Whole Numbers | Closure Property | Commutative Property

May 27, 24 05:41 PM

$Division Algorithm of a Whole Numbers$

Worksheet on Integers and the Number Line|Integers using a Number Line

May 27, 24 02:10 PM

$Worksheet on Integers and the Number Line$

Divide on a Number Line | Various Division Problems | Solved Examples

May 27, 24 11:43 AM

Multiplication using Number Lines | Multiplying on a Number Line

May 27, 24 11:28 AM

Solving the SAT problem using spiking neural P systems with coloured spikes and division rules

Research Paper
Open access
Published: 23 May 2024

Cite this article

You have full access to this open access article

Prithwineel Paul 1 na1 &
Petr Sosík 1 na1

Spiking neural P systems (SNPS) are variants of the third-generation neural networks. In the last few decades, different variants of SNPS models have been introduced. In most of the SNPS models, spikes are represented using an alphabet with just one letter. In this paper, we use a deterministic SNPS model with coloured spikes (i.e. the alphabet representing spikes contains multiple letters), together with neuron division rules to demonstrate an efficient solution to the SAT problem. As a result, we provide a simpler construction with significantly less class resources to solve the SAT problem in comparison to previously reported results using SNPSs.

Spiking Neural P Systems with Structural Plasticity: Attacking the Subset Sum Problem

Spiking neural p systems with structural plasticity.

Local Homogeneous Weighted Spiking Neural P Systems

Avoid common mistakes on your manuscript.

1 Introduction

Membrane computing is a well-known natural computing model. The computing models in membrane computing are inspired by the working of biological cells. In the last decades, many researchers have constructed different variants of membrane computing models inspired by different biological phenomena [ 1 ]. One such type of cell inspiring many computational models is the neuron. The structure and function of biological neurons communicating via sending impulses (spikes) was the main motivation behind the construction of a popular variant of membrane computing model known as the spiking neural P system (SNPS) [ 2 , 3 ]. Since SNNs (i.e. spiking neural networks) [ 4 ] belong to third-generation neural networks, SNPS models can also be considered third-generation neural networks.

Membrane computing models are mainly categorised into three types, i.e. (1) cell like; (2) tissue like; (3) neural like. One of the most popular directions of research in membrane computing is solving computationally hard problems using different variants of P systems. A comprehensive survey on the use of variants of membrane computing models for solving NP-hard problems, i.e. NP-complete (SAT, SUBSET-SUM) and PSPACE-complete problems (QSAT, Q3SAT) can be found in [ 5 , 6 ]. For instance, SNPS with pre-computed resources has been used to solve QSAT, Q3SAT problems [ 7 ], SUBSET-SUM problem [ 8 , 9 , 10 ], SAT & 3SAT problems [ 10 , 11 ] in a polynomial or even linear time. SNPS with neuron division and budding can solve the SAT problem in a polynomial time with respect to the number of literals n and the number of clauses m . Moreover, these SNP systems can solve the problem in a deterministic manner [ 12 , 13 ]. Similarly, an SNPS with budding rules [ 14 ] and an SNPS with division rules [ 15 ] can solve the SAT problem in polynomial time and a deterministic manner. Furthermore, SNPSs with structural plasticity and time-free SNPS models can solve the SUBSET-SUM problem in a feasible time [ 16 , 17 ]. In [ 18 ], it has been proved that SNPS with astrocytes producing calcium can solve the SUBSET-SUM problem in a polynomial time. Recently, a linear time uniform solution for the Boolean SAT problem using self-adapting SNPS with refractory period and propagation delay is derived in [ 19 ]. Finally, SNPS models have been used to solve maximal independent set selection problems from distributed computing [ 20 ].

In this paper, we construct a new variant of SNPS model, i.e. spiking neural P system with coloured spikes and division rules. The idea of coloured spikes was introduced by Song et al. [ 21 ] to simplify the construction of a SNPS solving complex tasks. Division rules were introduced for the first time in [ 12 , 22 ] to solve the SAT problem using SNPS with division rules and budding. Both the spiking rules and the division rules used here to solve the SAT problem are deterministic in nature. In this paper, we show that with this combined variant, we can solve the SAT problem efficiently using a lower number of steps as well as less amount of other resources.

The paper is organized in the following manner: in Sect. 2 , we discuss the structure and function of the SNP system with coloured spikes and neuron division. In Sect. 3 , we describe a solution to the SAT problem using this variant of SNPS. In Sect. 4 , we give a brief comparison of descriptional and computational complexity of two other SNPS models with division rules, in the amount of resources necessary to solve the SAT problem. Section 5 is conclusive in nature.

2 Spiking neural P system with coloured spikes and neuron division

In this section, we introduce the new variant of SNPS model, i.e. spiking neural P systems with coloured spikes and neuron division, which we mentioned in Sect. 1 . More precisely, this variant combines properties of two existing SNPS models, i.e. SNPS with neuron division [ 12 ] and SNPS with coloured spikes [ 21 ]. Division rules are used to obtain an exponential workspace in polynomial time to apply the strategy of trading space for time, while the use of coloured spikes allows for a simpler and more efficient construction of the SNPS. In the sequel we denote by L ( E ) the language associated to E , where E is a regular expression over an alphabet S .

Definition 1

A spiking neural P system with coloured spikes and neuron division of degree $m \ge 1$ is a construct of the form $\Pi = (S, H, syn, \sigma _1, \sigma _2, \ldots , \sigma _m, R,$ in , out ) where

$m \ge 1$ represents the initial degree, i.e. the number of neurons initially present in the system;

$S = \{a_1, a_2, \ldots , a_g\}, g \in \mathbb {N}$ is the alphabet of spikes of different colours;

H is the set containing labels of the neurons;

$syn \subseteq H \times H$ represents the synapse dictionary between the neurons where $(i, i) \notin syn$ for $i \in H$ .

$\sigma _1, \sigma _2, \ldots , \sigma _m$ are neurons initially present in the system, with $\{1,\dots ,m\}\subseteq H,$ where each neuron $\sigma _i = \langle n_1^{i}, n_2^{i}, \ldots , n_g^{i}\rangle ,$ for $1 \le i \le m,$ contains initially $n_{j}^{i} \ge 0$ spikes of type $a_j$ $(1 \le j \le g)$ ;

R represents the set containing the rules of the system $\Pi$ . Each neuron labelled $i\in H$ contains rules denoted by $[r]_i.$ The rules in R are divided into three categories:

Spiking rule: $[E / a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g} \rightarrow a_1^{p_1} a_2^{p_2} \ldots a_g^{p_g}; d]_i$ where $i \in H$ , E is a regular expression over S ; $n_j \ge p_j \ge 0$ $(1 \le j \le g)$ ; $d \ge 0$ is called delay. Furthermore, $p_j>0$ for at least one j , $1 \le j \le g.$

Forgetting rule: $[a_1^{t_1} a_2^{t_2} \ldots a_n^{t_n} \rightarrow \lambda ]_i$ where $i \in H$ , and $a_1^{t_1} a_2^{t_2} \ldots a_n^{t_n} \notin L(E)$ for each regular expression E associated with any spiking rule present in the neuron i .

Neuron division rule: $[E]_i \rightarrow []_j\,||\,[]_k$ where E is a regular expression over S and $i, j, k \in H$ .

in and out represent the input and output neurons, respectively.

A spiking rule $[E / a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g} \rightarrow a_1^{p_1} a_2^{p_2} \ldots a_g^{p_g}; d]_i$ is applicable when the neuron $\sigma _i$ contains spikes $a_1^{c_1} a_2^{c_2} \ldots a_n^{c_n} \in L(E)$ and $c_j \ge n_j$ $(1 \le j \le g)$ . After application of the rule, $n_j$ copies of the spike $a_j$ $(1\le j\le g)$ are consumed while $(c_j - n_j)$ copies remains inside the neuron $\sigma _i$ . Furthermore, $p_j$ spikes $(1\le j\le g)$ are sent to all neurons $\sigma _i$ is connected to. These are either neurons $\sigma _k$ such that $(i,k)\in syn,$ or neurons to which $\sigma _i$ inherited synapses during neuron division, as described bellow. If the delay $d = 0$ , then the spikes leave the neuron i immediately. However, if $d \ge 1$ and the rule is applied at time t , then the neuron i will be closed at step $t, t+1, t+2, \ldots , t+ d -1$ . During this phase, the neuron cannot receive any spike from outside nor can apply any rule. At step $(t + d)$ , the neuron spikes and it can also receive spikes from other neurons and apply a rule.

The spiking rule $[E / a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g} \rightarrow a_1^{p_1} a_2^{p_2} \ldots a_g^{p_g}; d]_i$ is simply written as $[a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g} \rightarrow a_1^{p_1} a_2^{p_2} \ldots a_g^{p_g}; d]_i$ if $E = a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g}$ . If $d = 0$ , then it becomes $[E/a_1^{n_1} a_2^{n_2} \ldots a_g^{n_g} \rightarrow a_1^{p_1} a_2^{p_2} \ldots a_g^{p_g}]_i$ .

A forgetting rule $[a_1^{t_1} a_2^{t_2} \ldots a_n^{t_n} \rightarrow \lambda ]_i$ is applicable when the neuron $\sigma _i$ contains exactly the spikes $a_1^{t_1} a_2^{t_2} \ldots a_n^{t_n}$ . Then all these spikes are consumed in the neuron $\sigma _i$ .

A division rule $[E]_i \rightarrow []_j\,||\,[]_k$ is applicable if a neuron $\sigma _i$ contains spikes $a_1^{c_1} a_2^{c_2} \ldots a_n^{c_n} \in L(E)$ . Then after application of the rule, two new neurons labelled j and k are created from $\sigma _i$ and the spikes are consumed. Child neurons contain developmental rules from R labelled j and k , respectively, and initially they do not contain any spikes. Also, child neurons inherit synaptic connections of the parent neuron. If there exists any connection $(\sigma _t, \sigma _i)$ (i.e. $\sigma _t$ is connected to $\sigma _i$ ), then after division there exist connections $(\sigma _t, \sigma _j)$ and $(\sigma _t, \sigma _k)$ . Similarly, if there exists a connection $(\sigma _i, \sigma _t)$ , then $(\sigma _j, \sigma _t)$ and $(\sigma _k, \sigma _t)$ will exist after division. Moreover, the child neurons will create synaptic connections which are provided by the synapse dictionary.

The configuration of the system provides information about the number of spikes present in the neurons, the synaptic connections with the other neurons and whether the neuron is open/closed (i.e. whether it can receive/send spikes). The SNPS models work as a parallel distributive computing model where the rules present in all neurons are applied in parallel synchronized manner and the configuration moves to the next configuration. Each computation starts from the initial configuration and stops at a final configuration (i.e. when no rules are further applicable in any of the neurons). If a neuron has more than one rule which is applicable in a given step, then one of these rules is non-deterministically chosen. However, in this work, such a situation never occurs and rules in the neurons are applied in a deterministic manner.

Since already the introductory variant of the SNPS presented in [ 2 ] is computationally universal in the Turing sense, and as our variant of the SNPS is an extension of this basic model, its computational universality follows by the results presented already in [ 2 ]. In the next section, we use the deterministic SNPS with coloured spikes and neuron division to obtain a uniform solution to the SAT problem in a linear time.

3 A solution to the SAT problem

Many decision problems have been solved using spiking neural P systems in uniform as well as semi-uniform ways [ 7 , 9 , 10 , 11 , 12 , 13 , 15 , 16 , 17 ]. Let M be a decision problem. If the problem M is solved in a semi-uniform manner, then for each instance I of M , a spiking neural P system $\Pi _{I, M}$ is constructed in polynomial time (with respect to the size of the instance I ). The structure and initial configuration of the system $\Pi _{I, M}$ depends on the instance I . Moreover, the system $\Pi _{I, M}$ halts (or it may spike a specified number of spikes within a time interval) if and only if I is a positive instance of the decision problem M . A uniform solution of M contains the family $\{\Pi _{M}(n)\}_{n \in \mathbb {N}}$ of SNP systems where for each instance $I \in M$ of size n , polynomial number of spikes based on n is introduced into a specified input neuron of $\Pi _{I, M}$ . Moreover, the system $\Pi _{I, M}$ halts if and only if I is a positive instance of M . The uniform solutions are strictly associated with the structure of the problem instead of being associated with only one instance of the decision problem. This feature makes the uniform solutions to decision problems more preferable than the semi-uniform solutions. Also, in order to obtain a semi-uniform solution, the SNP system does not require any specific input neuron. However, in the case of uniform solutions, the system must have a specified input neuron(s) which receives the description of an instance of the decision problem in the form of a spike train.

The SAT problem (or the Boolean satisfiability problem) [ 23 ] is a well-known NP-complete decision problem. Each instance is a formula in propositional logic with variables obtaining values TRUTH or FALSE . The SAT decision problem is the problem of determining whether there exists an assignment of truth values to the variables such that the whole formula evaluates to TRUTH .

Let us consider an instance represented by the formula $\gamma _{n, m} = C_1 \wedge C_2 \wedge \cdots \wedge C_m$ in the conjunctive normal form, where $C_i$ $(1 \le i \le m)$ represent the clauses. Each clause is a disjunction of literals of the form $x_j$ or $\lnot x_j$ , where $x_j$ are logical variables, $1\le j \le n.$ Moreover, the class of SAT instances with n variables and m clauses is denoted by SAT ( n , m ). So $\gamma _{n,m} \in SAT(n,m)$ . In order to solve the SAT problem, at first we have to encode the instance $\gamma _{n,m}$ using spikes in the SNPS, so that the encoded instance could be sent to the input neuron. In this work, we consider the SNPS model with coloured spikes, i.e. different variables are encoded by different types of spikes. The encoding of the instance $\gamma _{n,m}$ is as follows:

In addition to $\alpha _{i,j},$ the encoding of the instance contains other auxiliary spikes. The term $a^{n+1}$ is added at the beginning in order to give the system a necessary initial period during which it generates an exponential workspace with $2^n$ neurons. The encoding of each clause is separated by $a_c$ and the end of the encoding is identified by $a_f$ .

The spiking neural P system with coloured spikes and division rules solving the instances in SAT ( n , m ) is described below.

3.1 The SNPS description

The structure of the SNPS with coloured spikes and division rules is as follows: $\Pi _{n,m} = (S, H, syn, \sigma _{1_0}, \sigma _{1_0'}, \sigma _{n+1}, \sigma _{n+2}, \sigma _{n+3}, \sigma _{n+4}, \sigma _{n+5}, R, in, out)$ where

$S = \{ a_i, a_i'\ |\ 1\le i\le n\} \cup \{a, a_s, a_c, a_f\}.$

$H = \{i, i', i_0, i_0' \ |\ i = 1, 2, \ldots , n \}$ $\cup$ $\{ n+1, n+2, n+3, n+4, n+5\}$ $\cup$ $\{in, out\}$ $\cup$ $\{t_i, f_i\ |\ i = 1, 2, \ldots , n \}$ .

$syn = \{(i, t_i), (i', f_i)\ |\ i = 1, 2, \ldots , n\}$ $\cup$ $\{ (n+2, n+1), (n+2, n+3), (n+3, n+2), (n+4, n+2), (n+4, n+3) \}$ $\cup$ $\{ (in, 1_0), (in, 1_0'), (in, n+5), (n+5, t_1), (n+5, f_1) \}$ $\cup$ $\{(t_1, out), (f_1, out) \}.$

the initial configuration of the system contains neurons with labels in , out , $1_0, 1_0', n+1, n+2, n+3, n+4, n+5$ . The neurons with labels $1_0, 1_0', n+2, n+3$ and $n+4$ contain the spike a , and the remaining neurons contain no spike.

Rules in R are divided into four modules: (1) generating module; (2) input module; (3) checking module; (4) output module.

Rules in the generating module:

$[a]_{i_0} \rightarrow []_{i}\,||\,[]_{(i+1)_0}; i = 1, 2, \ldots , n-2$

$[a]_{(n-1)_0} \rightarrow []_{n-1}\,||\,[]_{n}$

$[a]_{i_0'} \rightarrow []_{i'}\,||\,[]_{(i+1)_0'}; i = 1, 2, \ldots , n-2$

$[a]_{(n-1)_0'} \rightarrow []_{(n-1)'}\,||\,[]_{n'}$

$[a]_{t_i} \rightarrow []_{t_{i+1}}\,||\,[]_{f_{i+1}}; i = 1, 2, \ldots , n-1$ ;

$[a]_{f_i} \rightarrow []_{t_{i+1}}\,||\,[]_{f_{i+1}}; i = 1, 2, \ldots , n-1$ ;

$[a]_{n+1} \rightarrow []_{t_1}\,||\,[]_{f_1}$

$[a \rightarrow a]_{n+2}$

$[a^{2} \rightarrow \lambda ]_{n+2}$

$[a \rightarrow a]_{n+3}$

$[a^{2} \rightarrow \lambda ]_{n+3}$

$[a \rightarrow a; n+1]_{n+4}$

$[S^* / a_c \rightarrow a_c]_{n+5}$

$[S^* / a_f \rightarrow a_f]_{n+5}.$

Rules in the input module:

$[a_i \rightarrow a_i]_{in}; i = 1, 2, \ldots , n$

$[a_i' \rightarrow a_i']_{in}; i = 1, 2, \ldots , n$

$[a \rightarrow a]_{in}$ ;

$[a_c \rightarrow a_c]_{in}$ ;

$[a_f \rightarrow a_f]_{in}$ ;

$[S^{*} / a_i \rightarrow a]_i; i = 1, 2, \ldots , n$

$[S^{*} / a_i' \rightarrow a]_{i'}; i = 1, 2, \ldots , n$

Note: the last two rules are not seen in Fig. 1 as the neurons $\sigma _i$ , $i = 1, 2, \ldots , n,$ appear during the generating phase.

Rules in the checking module:

$[a_saa / a \rightarrow a_s]_{t_n}$

$[a_sa_c \rightarrow \lambda ]_{t_n}$

$[a_sa_ca / a_ca \rightarrow a_s]_{t_n}$

$[a_sa_f \rightarrow a]_{t_n}$

$[a_saa / a \rightarrow a_s]_{f_n}$

$[a_sa_c \rightarrow \lambda ]_{f_n}$

$[a_sa_ca / a_ca \rightarrow a_s]_{f_n}$

$[a_sa_f \rightarrow a]_{f_n}.$

Rules in the output module:

$[a_s^{+} a^{+} / a \rightarrow a]_{out}.$

The initial structure of the SNPS with coloured spikes and division rules solving an instance of the SAT problem using contains 9 neurons (see Fig. 1 ). Computation of the SNPS is divided into four stages: (1) generating; (2) input; (3) checking; (4) output.

Initial structure of the SNPS solving the SAT problem

In the generating stage, the division rules are used to create an exponential number of neurons which are further used during the input and checking stages. In the input stage, the input neuron receives the encoded instance of the SAT problem. This stage overlaps with the checking stage during which the SNPS verifies whether any assignment of values of the variables $x_1, x_2, \ldots , x_n$ satisfies all the clauses $C_i$ $(1 \le i \le m)$ present in the proposition formula $\gamma _{n,m}$ . Finally, if the output neuron spikes, it confirms that the formula $\gamma _{n,m}$ is satisfiable.

3.2 Generating stage

Neurons $1_0$ and $1_0'$ contain initially the spike a and the rule $[a]_{1_0} \rightarrow []_{1}\,||\,[]_{2_0}$ and $[a]_{1_0'} \rightarrow []_{1'}\,||\,[]_{2_0'},$ respectively. Thus, the neuron $\sigma _{1_0}$ creates two neurons with labels 1 and $2_0,$ and the neuron $\sigma _{1_0'}$ creates two neurons with labels $1'$ and $2_0'$ at time $t=1$ .

The input neuron has synaptic connections to the neurons with labels $1_0$ and $1_0',$ which are inherited by the neurons $1, 1',$ $2_0$ and $2_0'.$ At times $i=1,2,\dots ,n+1,$ the input neuron receives the spike a from the input spike train and at times $i=2,3,\dots ,n-1$ it sends the spike to neurons $i_0$ and $i_0'$ $(2\le i\le n-1).$ At times $i=n,$ $n+1$ and $n+2,$ the input neuron sends spikes, too, but no neurons with labels $i_0$ and $i_0'$ $(n\le i\le n+2$ exist.)

Neurons $i_0$ and $i_0'$ $(2\le i\le n-2)$ contain the rule $[a]_{i_0} \rightarrow []_{i}\,||\,[]_{(i+1)_0}$ and $[a]_{i_0'} \rightarrow []_{i'}\,||\,[]_{(i+1)_0'},$ i.e. the neuron $\sigma _{i_0}$ creates two neurons with labels i and $(i+1)_0,$ and the neuron $\sigma _{i_0'}$ creates two neurons with labels $i'$ and $(i+1)_0'$ $(2 \le i \le n-1).$

Finally, at step $t=n-1,$ neurons with labels $(n-1)_0$ and $(n-1)_0'$ divide and create neurons with labels $n-1,$ n , $(n-1)'$ and $n'.$ So after application of all these division rules, there is a layer of neurons $\sigma _i,$ $\sigma _{i'}$ $(1\le i\le n)$ shown in Fig. 7 , and the input neuron has synaptic connections to all of them.

Simultaneously, the neurons with labels $n+1, n+2, n+3$ and $n+4$ create subsequently $2^{n}$ neurons which will be used in the checking stage. The circuit controlling the generating stage is depicted in Fig. 2 . Initially, the neurons $n+2, n+3$ and $n+4$ contain one spike. At time $t = 1$ , $\sigma _{n+2}$ and $\sigma _{n+3}$ spike and $\sigma _{n+1}$ receives a spike at time $t = 2$ . At $t = 2$ , the rule $[a]_{n+1} \rightarrow []_{t_1}\,||\,[]_{f_1}$ is applied (Fig. 3 ). So at $t = 3$ , two new neurons with labels $t_1$ and $f_1$ are created (Fig. 4 ).

Details of the generating module producing the exponential workspace of $2^n$ neurons in the first n computational steps of the SNPS

Structure of the SNPS at time $t = 2$

Structure of the SNPS at time $t = 3$

Note that the neuron $\sigma _1$ (resp. $\sigma _{1'}$ ) is connected to $\sigma _{t_1}$ (resp. $\sigma _{f_1}$ ) using the synaptic connections from synapse dictionary. Moreover, $\sigma _{t_1}$ and $\sigma _{f_1}$ are connected to the output neuron with the synaptic connections from the synapse directory (see Fig. 4 ). The neuron $\sigma _{t_1}$ contains the rule $[a]_{t_1} \rightarrow []_{t_2}\,||\,[]_{f_2}$ and neuron $\sigma _{f_1}$ contains $[a]_{f_1} \rightarrow []_{t_2}\,||\,[]_{f_2}$ .

At the same time $t=3,$ neurons $\sigma _{t_1}$ and $\sigma _{f_1}$ receive the spike a from $\sigma _{n+2}$ . Hence, at $t = 4$ , each of $\sigma _{t_1}$ and $\sigma _{f_1}$ is divided into $\sigma _{t_2}$ and $\sigma _{f_2}$ . Again, these neurons receive one spike from $\sigma _{(n+2)}$ and they are divided at the next step. This process will continue until $t = n+2$ . Newly created neurons $t_i, f_i$ $(1\le i\le n)$ will also get further synapses due to the synapse dictionary, as described above. After $(n+2)$ steps, we will show a system in Fig. 7 .

Finally, the rule $a \rightarrow a; n+1$ in $\sigma _{n+4}$ is applied at time $t = n+2$ and thus both $\sigma _{n+2}$ and $\sigma _{n+3}$ receive one spike at $t = n+3$ . Next, the rule $a^{2} \rightarrow \lambda$ is applied and both spikes in $\sigma _{n+2}$ and $\sigma _{n+3}$ are consumed. So no spikes remain inside them and they are inactive from now on.

3.3 Input stage

Recall that the input neuron receives the encoding of an instance of the SAT problem with n variables and m clauses, i.e. $\gamma _{n,m}$ , where

The encoding of each clause is ended by $a_c$ and after the input is completely read, it ends with $a_f$ . The initial buffer $a^{n+1}$ is used to delay the input of the clause by $n+1$ steps, giving the SNPS enough time to generate $2^{n}$ checking neurons. The input neuron in has the following rules: (1) $a \rightarrow a;$ (2) $a_i \rightarrow a_i\ (1 \le i \le n);$ (3) $a_i' \rightarrow a_i'\ (1 \le i \le n);$ (4) $a_c \rightarrow a_c;$ (5) $a_f \rightarrow a_f$ . Initially, the input neuron is empty and when it receives $a, a_i, a_i', a_c$ or $a_f$ as input, it spikes and sends the same spike to neurons with labels $i, i'$ $(1 \le i \le n)$ and $n+5$ .

At time $t = n + 2$ , the input neuron receives $\alpha _{1,1}$ as input. Since the input neuron contains the rules $[a_i \rightarrow a_i]_{in}; [a_i' \rightarrow a_i']_{in}$ $(1 \le i \le n)$ , it will spike immediately. The neurons with label i contain the rule $[S^{*} / a_i \rightarrow a]_i$ $(1 \le i \le n)$ and neurons with label $i'$ contain the rule $[S^{*} / a_i' \rightarrow a]_{i'}$ $(1 \le i \le n)$ . These rules are activated upon the existence of the literal $x_i$ (resp. $\lnot x_i$ ) in a clause. If $\sigma _i$ spikes using the rule $[S^{*} / a_i \rightarrow a]_i$ , it signals that the literal $x_i$ is present in a clause. Similarly, the use of the rule $[S^{*} / a_i' \rightarrow a]_{i'}$ in $\sigma _{i'}$ signals the presence of $\lnot x_i$ in a clause.

3.4 Checking stage

After the generating stage, the input neuron is connected to neurons $\sigma _i$ and $\sigma _{i'}\ (1 \le i \le n)$ . These neurons, in turn, are connected to the checking layer consisting of $2^n$ neurons labelled $t_n$ or $f_n,$ see Fig. 7 . Each of the checking neurons $\sigma _{t_n}$ or $\sigma _{f_n}$ has exactly n incoming synapses from the input neurons $\sigma _i$ or $\sigma _{i'}\ (1 \le i \le n)$ . These synapses represent one of the $2^{n}$ possible assignments of ‘TRUTH’ or ‘FALSE’ to the n variables of the formula. The structure of these synapses was created by either inherited synapses or by the synapse dictionary during the generating stage. The incoming synapses are indicated under checking neurons in Figs. 4 , 5 , 6 , and 7 by expressions in parentheses. Let us consider the assignment $t_1 t_2 f_3 \ldots f_n$ (i.e. the first two variables have ‘TRUTH’ and the remaining ones have ‘FALSE’). The corresponding checking neuron has synapses from neurons $\sigma _1,$ $\sigma _2,$ $\sigma _3',$ $\dots ,$ $\sigma _n',$ in the input module.

Structure of the SNPS at time $t = 4$

Structure of the SNPS at time $t = 5$

Structure of the SNPS at time $t = n+2$

The input module receives encoded clauses one by one. Spiking of the neuron $\sigma _i$ in the input module signals the presence of the literal $x_i$ in the clause, and spiking of the neuron $\sigma _{i'}$ signals the presence of the literal $\lnot x_i.$ Therefore, each of the neurons $\sigma _{t_n}$ or $\sigma _{f_n}$ obtains one or more spike a if its assignment satisfies the clause. These neurons contain rules $(1) a_s a a / a \rightarrow a_s;\ (2) a_s a_c \rightarrow \lambda ;\ (3) a_s a_c a / a_c a \rightarrow a_s;\ (4) a_s a_f \rightarrow a$ .

Initially, neurons in the checking module contain the spike $a_s.$ If it receives the spike a from the input module, no rule can be applied. When another a spike comes, the rule $a_s aa / a \rightarrow a_s$ is applied and only one spike a remains in the neuron. When the encoding of the clause is read completely, the spike $a_c$ is received from $\sigma _{n+5}$ . If the assignment of a checking neuron satisfies the clause, the neuron now has the spikes $a_s a_c a$ and the rule $a_s a_c a / a_c a \rightarrow a_s$ is applied. Otherwise, the neuron contains the spike $a_s a_c$ and they are consumed by the rule $a_s a_c \rightarrow \lambda$ . Since the neuron looses the spike $a_s$ , no further computation will take place inside it.

3.5 Output stage

The output neuron can receive spikes $a_s$ due to the application of the rules $a_saa / a \rightarrow a_s$ and $a_sa_ca / a_ca \rightarrow a_s$ in checking neurons during the checking stage. However, these spikes are ignored. Finally, when the formula is completely read, the checking neurons receive the spike $a_f$ from $\sigma _{n+5}$ . If any of them still has the spike $a_s$ (meaning that its assignment satisfies all clauses), it spikes using the rule $a_sa_f \rightarrow a$ and the spike a is sent to the output neuron. Next, the rule $a_s^{+} a^{+} / a \rightarrow a$ is applied in the output neuron, confirming that the formula is satisfiable.

4 Discussion

In this section, we compare parameters of our solution to the SAT problem using a SNPS with coloured spikes and division rules with two other published papers [ 13 , 15 ] presenting similar solutions to the SAT with SNP systems. Both papers use neuron division rules, the authors of [ 13 ] use also neuron dissolution rules. We compare five parameters of descriptional complexity of the used SNP systems and also the running time complexity. The results are summarized in the table below assuming a solution to an instance of SAT ( n , m ), i.e. with m clauses and n variables.

A more detailed analysis of the running time shows that the generation stage in our paper requires $(n+1)$ steps when the exponential workspace is created. The total number of steps required for the following input stage reading the encoded formula via the input neuron is $m(n+1) + 1.$ , The checking stage largely overlaps with the input one and requires two more steps to complete. Finally the output stage required only one step.

It follows that all descriptional complexity parameters used in our model have significantly lower values than in the two compared papers. More specifically, the number of neurons, number of neuron labels, size of the synapse dictionary and number of rules used in our solution are significantly lower than in previous solutions and we are able to achieve this result using only 5 initial spikes. Especially, the number of rules is linear to n , while in the previously reported solutions it is quadratic or even exponential. Note that the coloured spikes largely help to organize the work of the system and allow for these simplifications.

The only exception is the running time which is $\mathcal {O}(n+m)$ in [ 13 ], while our SNPS runs in time $\mathcal {O}(nm).$ The explanation is simple: the authors of [ 13 ] use m input neurons and a special encoding of the formula where each clause is sent in parallel to the n designated input neuron in just one step. Therefore, the input stage in [ 13 ] takes only $\mathcal {O}(m)$ steps. We conjecture that such an input encoding can be employed also in our construction, diminishing the total running time to $\mathcal {O}(n+m).$

5 Conclusion

We presented a deterministic spiking neural P system with coloured spikes and division rules which has been used to solve the SAT problem in linear time. We have shown that our model uses significantly less resources than those reported in [ 13 , 15 ] to solve the SAT problem. It is fair to note that we use a linear number of different spikes with respect to the number n of variables in SAT, while the two mentioned papers use just one type of spike. However, most types of spikes in our construction is used just to encode the input formula. We could use a similar input encoding and an input module with multiple input neurons as that in [ 13 ] with only a few changes which would lower the number of different spikes (= colours) in our model to 5. Furthermore, this input module would restrict our running time to $\mathcal {O}(n+m).$ This is left for future research. As another possible future research direction one could focus on an efficient solution to PSPACE-complete problems using a similar SNPS model as that discussed in this paper.

Data availability

No datasets were generated or analysed during the current study.

Paun, G., Rozenberg, G., & Salomaa, A. (2010). The Oxford handbook of membrane computing . Oxford University Press Inc.

Book Google Scholar

Ionescu, M. ., Păun, G. ., & Yokomori, T. . (2006). Spiking neural P systems. Fundamenta Informaticae, 71 (2–3), 279–308.

MathSciNet Google Scholar

Leporati, A., Mauri, G., & Zandron, C. (2022). Spiking neural P systems: Main ideas and results. Natural Computing, 21 (4), 629–649.

Article MathSciNet Google Scholar

Ghosh-Dastidar, S., & Adeli, H. (2009). Spiking neural networks. International Journal of Neural Systems, 19 (04), 295–308.

Article Google Scholar

Song, B., Li, K., Orellana-Martín, D., Pérez-Jiménez, M. J., & Pérez-Hurtado, I. (2021). A survey of nature-inspired computing: Membrane computing. ACM Computing Surveys (CSUR), 54 (1), 1–31.

Sosík, P. (2019). P systems attacking hard problems beyond NP: A survey. Journal of Membrane Computing, 1 , 198–208.

Ishdorj, T.-O., Leporati, A., Pan, L., Zeng, X., & Zhang, X. (2010). Deterministic solutions to QSAT and Q3SAT by spiking neural P systems with pre-computed resources. Theoretical Computer Science, 411 (25), 2345–2358.

Gutiérrez Naranjo, M. Á., & Leporati, A. (2008). Solving numerical NP-complete problems by spiking neural P systems with pre-computed resources. In Proceedings of the Sixth Brainstorming Week on Membrane Computing (pp. 193–210). Sevilla, ETS de Ingeniería Informática, 4-8 de Febrero, 2008

Leporati, A., & Gutiérrez-Naranjo, M. A. (2008). Solving Subset Sum by spiking neural P systems with pre-computed resources. Fundamenta Informaticae, 87 (1), 61–77.

Leporati, A., Mauri, G., Zandron, C., Păun, G., & Pérez-Jiménez, M. J. (2009). Uniform solutions to SAT and Subset Sum by spiking neural P systems. Natural computing, 8 (4), 681.

Ishdorj, T.-O., & Leporati, A. (2008). Uniform solutions to SAT and 3-SAT by spiking neural P systems with pre-computed resources. Natural Computing, 7 , 519–534.

Pan, L., Păun, G., & Pérez-Jiménez, M. J. (2011). Spiking neural P systems with neuron division and budding. Science China Information Sciences, 54 , 1596–1607.

Zhao, Y., Liu, X., & Wang, W. (2016). Spiking neural P systems with neuron division and dissolution. PLoS One, 11 (9), 0162882.

Ishdorj, T.-O., Leporati, A., Pan, L., & Wang, J. (2010). Solving NP-complete problems by spiking neural P systems with budding rules. In Membrane Computing: 10th International Workshop, WMC 2009, Curtea de Arges, Romania, August 24–27, 2009. Revised Selected and Invited Papers 10 .(pp. 335–353). Springer.

Wang, J., Hoogeboom, H. J., & Pan, L. (2011). Spiking neural P systems with neuron division. In Membrane Computing: 11th International Conference, CMC 2010, Jena, Germany, August 24–27, 2010. Revised Selected Papers 11 (pp. 361–376). Springer.

Cabarle, F. G. C., Hernandez, N. H. S., & Martínez-del-Amor, M. Á. (2015). Spiking neural P systems with structural plasticity: Attacking the Subset Sum problem. In: Membrane Computing: 16th International Conference, CMC 2015, Valencia, Spain, August 17–21, 2015, Revised Selected Papers 16 (pp. 106–116). Springer.

Song, T., Luo, L., He, J., Chen, Z., & Zhang, K. (2014). Solving Subset Sum problems by time-free spiking neural P systems. Applied Mathematics & Information Sciences, 8 (1), 327.

Aman, B. (2023). Solving Subset Sum by spiking neural P systems with astrocytes producing calcium. Natural Computing, 22 , 3–12.

Zhao, Y., Liu, Y., Liu, X., Sun, M., Qi, F., & Zheng, Y. (2022). Self-adapting spiking neural P systems with refractory period and propagation delay. Information Sciences, 589 , 80–93.

Xu, L., & Jeavons, P. (2013). Simple neural-like P systems for maximal independent set selection. Neural Computation, 25 (6), 1642–1659.

Song, T., Rodríguez-Patón, A., Zheng, P., & Zeng, X. (2017). Spiking neural P systems with colored spikes. IEEE Transactions on Cognitive and Developmental Systems, 10 (4), 1106–1115.

Pan, L., Paun, G., & Pérez Jiménez, M. J. (2009). Spiking neural P systems with neuron division and budding. In Proceedings of the Seventh Brainstorming Week on Membrane Computing (Vol. II, pp. 151–167). Sevilla, ETS de Ingeniería Informática, 2–6 de Febrero, 2009.

Rintanen, J. (2009). Planning and SAT. Handbook of Satisfiability, 185 , 483–504.

Google Scholar

Download references

Acknowledgements

This work was supported by the Silesian University in Opava under the Student Funding Plan, project SGS/9/2024.

Open access publishing supported by the National Technical Library in Prague.

Author information

Prithwineel Paul and Petr Sosík have contributed equally to this work.

Authors and Affiliations

Faculty of Philosophy and Science, Institute of Computer Science, Silesian University in Opava, Bezručovo náměstí 1150/13, 74601, Opava, Czech Republic

Prithwineel Paul & Petr Sosík

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Petr Sosík .

Ethics declarations

Conflict of interest.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Paul, P., Sosík, P. Solving the SAT problem using spiking neural P systems with coloured spikes and division rules. J Membr Comput (2024). https://doi.org/10.1007/s41965-024-00153-0

Download citation

Received : 12 January 2024

Accepted : 24 April 2024

Published : 23 May 2024

DOI : https://doi.org/10.1007/s41965-024-00153-0

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Spiking neural P system
Neuron division
Coloured spikes
SAT problem

Mathematics Subject Classification

Find a journal
Publish with us
Track your research

IMAGES

Problem-Solving Strategies: Definition and 5 Techniques to Try
Division Problem Solving
5 Fun Division Word Problems
Solving Division Problems Using an Algorithm
Problem Solving
An Overview Of 9 Step Problem Solving Model

VIDEO

3rd Grade 6.1
unit 7 lesson 8 and 9 area model and standard division algorithm
Division Working Model for Grade 3 Maths Introduction to division
Problem Solving Model
PM Three Sixty Conference: Unleash Your Project Management Potential
Problem Solving lesson #3

COMMENTS

Problem Solving
This lesson shows how to "Act It Out" to model division. Easy lesson. :)
Division with area models (video)
But we can divide 56 by eight. We know that eight times seven is 56. So what you could do is, you could break this rectangle into the 856 square units, you could break it up in to 800 square units, and then another 56, and another 56 square units. So once again, we broke it up in to eight hundreds, and then 56 ones.
Learn Division
Get started using GeoGebra today. Create a free account so you can save your progress any time and access thousands of math resources for you to customize and share with others. Explore over 10 free and ready-to-use GeoGebra resources for grades 4-8 to improve your skills in estimating and solving division problems and using rules for divisibility.
Division Model...... How To Draw Models to Solve Problems on Divide
Basic Division Model. Here are the basic models. You can also check out the other variations of the division model. To divide 24 by 3, draw 3 boxes to represent 3 groups and put 24 as the number to represent to total for the 3 groups. For this model, there are a few ways to draw it. They are presented below.
PDF Problem Solving • Model Division
who will travel in each van. Describe how to act out the problem to solve. Step 1 Start with 35 counters. Step 2 Make 5 equal groups. Place. counter at a time in each group until all 35 counters are used. Step 3 Count the number of counters in each group. 7. So, 7 people will travel in each van.
Division models: two ways of thinking of division
Lesson 3: Two ways of thinking of division. There are essentially two ways of thinking of division: Partition division (also known as partitive, sharing and grouping division) is a way of understanding division in which you divide an amount into a given number of groups. If you are thinking about division this way, then 12 ÷ 3 means 12 things ...
Division Worksheets
Take a look at our long division problems worksheet generators. This generator will generate your own worksheets from 2-digits by 1-digit to 5-digits by 2-digits. You can also create your own long division worksheets with money amounts from up to $10 by a single digit to up to $100,000 by 2-digits.
Teaching Area Model Division to 4th Graders
Solving Word Problems With Area Model. Once children are comfortable with using the area model to solve division problems, you can introduce word problems that require division where the area model can also be applied. First, remind students that we need to identify the key question that is being asked in the problem.
PDF Name Lesson 6.1 Model Division
Problem Solving • Model Division COMMON CORE STANDARD—3.OA.A.3 Represent and solve problems involving multiplication and division. 5. WRITE Math Write a word problem about equal groups and act it out to solve. Lesson 6.1 Practice and Homework. 77 7 7 7 7 7 7 7 7 1324 65 Piano Practice Hours
Division
Unit test. Level up on all the skills in this unit and collect up to 1,400 Mastery points! Start Unit test. Do you like breaking things apart? Then you're going to love learning about division! We'll use place value, area models, and estimation techniques to make dividing by 1-digit numbers a breeze. In this unit, you will even get the inside ...
Division Models Worksheets
Recapitulate three division methods with this set of interesting 3-in-1 activity worksheet pdfs. Solve for the quotient by representing each division equation as a grouping model, an array model and on a number line. Visually represent the division equation as a rectangle with these level 1 area models.
Division Problems: Different Models and Examples
1. Division Problems: Repetition. This is the first type of division problem you are going to learn to do. For example: In my living room, there are 120 books in total, placed on 6 shelves. Knowing that each shelf has the same number of books, calculate how many books there are on each shelf. Find:
Multiplication and division
Unit test. Test your understanding of with these NaN questions. Start test. In this topic, we will multiply and divide whole numbers. The topic starts with 1-digit multiplication and division and goes through multi-digit problems. We will cover regrouping, remainders, and word problems.
Thinking Blocks Multiplication and Division
Use equations with a symbol for the unknown number to represent the problem. Solve two-step word problems using the four operations. Represent problems using equations with a letter standing for the unknown quantity. Play Thinking Blocks Multiplication at Math Playground! Model and solve word problems with multiplication and division.
What Is Area Model Division ⭐ Definition, Examples, Facts
This approach improves mathematical comprehension, problem-solving skills, and logical reasoning abilities. ... we can find the width (the quotient) by using the area model division. Practice Problems on Area Model Division. Here are a few practice problems: Divide 24 by 4 using area model division. Use the area model division to divide 30 by 5.
Division Worksheets
Division worksheets including division facts and long division with and without remainders. Division Worksheets. ... used it is because it is an efficient and beautiful algorithm that will allow you to solve some of the most difficult division problems that even base ten blocks couldn't touch. It works equally well for decimals and whole ...
5th Grade Math 2.9, Word Problem Solving, Division Using Bar Models
The strategy "draw a diagram" can help us solve division problems. We can draw a diagram, such as a bar model, to help us organize the information in a way t...
Third grade Lesson Division Models to Solve Problems
LESSON 1: Building A Division Model; LESSON 2: Division Models to Solve Problems; LESSON 3: Creating Word Problems With Division; ... In order for students to develop fluency in solving division problems I feel it's essential to give them ample time to develop strategies. The problems use student names and real world situations so that students ...
Multiplication and Division Models and Strategies
Bar models are a great way to help students show their thinking when problem solving, especially when solving two-step problems. Image: Wikipedia.org. Number Lines: Number lines allow students to begin understanding the abstract stage of multiplication and division. Students begin to connect skip counting and multiples of a number to finding ...
Using Bar Models for Multiplication and Division
Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. Suggested Workbook Series. Math in Focus workbook (3A) Chapter 9 - Using Bar Models: Multiplication and Division (pages 159 to 180)
Problem Solving by Using Multiplication to Solve Division Problems
The 5 in this problem represents the number we are solving for." Model a few more examples on the overhead or board. Start out with problems using smaller numbers until students begin to see a pattern of how a division equation has a related multiplication sentence. ... Model how to do the division problem with counting cubes or counting ...
Examples on Word Problems on Division
Solution: Total number of apples = 63. There are 9 friends of seats on the bus. To find how many apples Tom gave to each of his friends, divide the total number of apples by the number of friends. We get, divide 63 by 9. 63 ÷ 9 = 7. Therefore, Tom gives 7 apples to each of his friends. Answer: 7 Apples. 7.
Problem-Solving Models: What They Are and How To Use Them
Here is a six-step process to follow when using a problem-solving model: 1. Define the problem. First, determine the problem that your team needs to solve. During this step, teams may encourage open and honest communication so everyone feels comfortable sharing their thoughts and concerns.
Solving the SAT problem using spiking neural P systems with ...
The idea of coloured spikes was introduced by Song et al. to simplify the construction of a SNPS solving complex tasks. Division rules were introduced for the first time in [12, 22] to solve the SAT problem using SNPS with division rules and budding. Both the spiking rules and the division rules used here to solve the SAT problem are ...

Upper Elementary

Creating Division Equations Using Visual Models

Multiplication and Division Estimation Game

Estimating Products of 2-digit Numbers

Division Problems with Remainders

Long Division With One-Digit Divisors and Remainders

Division Word Problems

Multiplication and Division with Multiples of Powers of Ten

Multiplying Negative Numbers

Card Sort: Multiplying and Dividing Integers

Community Resources

Get started using GeoGebra today

Basic Division Model

Division Worksheets ÷ Hub Page

Division Learning

Division Worksheets by Grade

Division Facts Worksheets

Division Word Problems

Second Grade Division

3rd Grade Division

4th Grade Division

5th Grade Division

Understanding Division Worksheets

Division Flashcards

Multiplication & Division Times Table Charts

Division Practice Area

Division (and multiplication) Worksheet Generator

Division Facts to 10x10 Sheets (3rd & 4th Grade)

Division Related Facts 10s and 100s (4th & 5th Grade)

Division Related Facts Decimals (5th & 6th Grade)

Dividing Negative Numbers (6th Grade)

Long Division Worksheets and Support

Long Division Support

Quickinks to ...

Randomly Generated Long Division Problems Worksheet Generator

Long Division 2 Digits by 1 Digit (3rd Grade)

Long Division 3 & 4 Digits by 1 Digit (4th Grade)

Long Division by 2 Digits (5th Grade)

Long Division by Decimals (6th Grade)

Fun Division Games

Subscribe to Math Salamanders News

Math-Salamanders.com

New! Comments

Teaching Area Model Division to 4th Graders

What Is Area Model Division (4th Grade)?

How to Teach Area Model Division (4th Grade)

How to Perform Area Model Division (4th Grade)

Why We Don’t Always Break Up Dividends This Much…

Solving Word Problems With Area Model

Activities to Practice Area Model Division

Area Model Division Task Cards

Before You Leave…

Share this:

Division using Models

Unit 3: Multiplication and division

Multiplication intro

Multiplication facts

Properties of multiplication

Multiplying by tens

Multiplication by 10s, 100s, and 1000s

Multiplication: place value and area models

Multi-digit multiplication

Relating multiplication and division

Division intro

Division facts

Division problems that work out nicely

Division: place value and area

Multi-digit division (no remainders)

Multi-digit division (remainders)

Multiplication and division word problems

Area Model Division – Definition, Examples, Facts

What is Area Model Division?

Definition of Area Model Division

How Does Area Model Division Work?

Benefits and Uses of Area Model Division

Examples of Area Model Division

Steps in Area Model Division

Properties and Characteristics of Area Model Division

Comparing Area Model Division with Other Division Models

Applying the Area Model Division in Real Life Context