hypothesis math calculator

Hypothesis Testing Calculator

Type ii error.

The first step in hypothesis testing is to calculate the test statistic. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. If σ is known, our hypothesis test is known as a z test and we use the z distribution. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. To switch from σ known to σ unknown, click on $\boxed{\sigma}$ and select $\boxed{s}$ in the Hypothesis Testing Calculator.

Next, the test statistic is used to conduct the test using either the p-value approach or critical value approach. The particular steps taken in each approach largely depend on the form of the hypothesis test: lower tail, upper tail or two-tailed. The form can easily be identified by looking at the alternative hypothesis (H a ). If there is a less than sign in the alternative hypothesis then it is a lower tail test, greater than sign is an upper tail test and inequality is a two-tailed test. To switch from a lower tail test to an upper tail or two-tailed test, click on $\boxed{\geq}$ and select $\boxed{\leq}$ or $\boxed{=}$, respectively.

In the p-value approach, the test statistic is used to calculate a p-value. If the test is a lower tail test, the p-value is the probability of getting a value for the test statistic at least as small as the value from the sample. If the test is an upper tail test, the p-value is the probability of getting a value for the test statistic at least as large as the value from the sample. In a two-tailed test, the p-value is the probability of getting a value for the test statistic at least as unlikely as the value from the sample.

To test the hypothesis in the p-value approach, compare the p-value to the level of significance. If the p-value is less than or equal to the level of signifance, reject the null hypothesis. If the p-value is greater than the level of significance, do not reject the null hypothesis. This method remains unchanged regardless of whether it's a lower tail, upper tail or two-tailed test. To change the level of significance, click on $\boxed{.05}$. Note that if the test statistic is given, you can calculate the p-value from the test statistic by clicking on the switch symbol twice.

In the critical value approach, the level of significance ($\alpha$) is used to calculate the critical value. In a lower tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the lower tail of the sampling distribution of the test statistic. In an upper tail test, the critical value is the value of the test statistic providing an area of $\alpha$ in the upper tail of the sampling distribution of the test statistic. In a two-tailed test, the critical values are the values of the test statistic providing areas of $\alpha / 2$ in the lower and upper tail of the sampling distribution of the test statistic.

To test the hypothesis in the critical value approach, compare the critical value to the test statistic. Unlike the p-value approach, the method we use to decide whether to reject the null hypothesis depends on the form of the hypothesis test. In a lower tail test, if the test statistic is less than or equal to the critical value, reject the null hypothesis. In an upper tail test, if the test statistic is greater than or equal to the critical value, reject the null hypothesis. In a two-tailed test, if the test statistic is less than or equal the lower critical value or greater than or equal to the upper critical value, reject the null hypothesis.

When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. There are two types of errors you can make: Type I Error and Type II Error. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true.

Hypothesis testing is closely related to the statistical area of confidence intervals. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Confidence intervals can be found using the Confidence Interval Calculator . The calculator on this page does hypothesis tests for one population mean. Sometimes we're interest in hypothesis tests about two population means. These can be solved using the Two Population Calculator . The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.

Hypothesis Testing Calculator Online

Hypothesis testing is a foundational method used in statistics to infer the validity of a hypothesis about a population parameter. The Hypothesis Testing Calculator facilitates this process by automating the computations necessary for the t-test , a method used to compare sample means against a hypothesized mean or against each other. Let’s delve into the formulas this calculator uses to execute one-sample and two-sample t-tests.

One-Sample t-Test

This test is used to determine if the mean (x̄) of your sample is statistically different from a hypothesized population mean (μ₀).

• t is the test statistic
• x̄ is the sample mean
• μ₀ is the hypothesized population mean
• s is the sample standard deviation
• n is the sample size (number of observations)

Two-Sample t-Test

This formula compares the means of two independent groups (x̄₁ and x̄₂), with variations for equal and unequal variances.

Equal Variances:

• x̄₁ and x̄₂ are the means of the first and second sample, respectively
• s pooled is the pooled standard deviation (calculated from both samples)
• n₁ and n₂ are the sizes of the first and second sample, respectively

Unequal Variances (Welch’s t-Test):

t = (x̄₁ – x̄₂) / (√((s₁² / n₁) + (s₂² / n₂)))

• x̄₁ is the mean of the first sample
• x̄₂ is the mean of the second sample
• s₁ and s₂ are the standard deviations of the first and second sample, respectively

Table of Critical t-Values

The following table provides critical t-values for different confidence levels and degrees of freedom which are typically use to determine the cutoff points at which the null hypothesis is reject.

These values are crucial in hypothesis testing as they help define the threshold for significance, assisting users of the calculator in interpreting their results accurately.

Consider a scenario where a school administrator wants to test if the average test score of the students this semester differs from a hypothesized mean of 70%. Using the one-sample t-test:

• Sample mean (x̄) = 74%
• Hypothesized mean (μ₀) = 70%
• Sample standard deviation (s) = 8%
• Sample size (n) = 36

Using the one-sample t-test formula:

t = (74 – 70) / (8 / √36) = (4 / 1.333) = 3.00

The calculated t-value is 3.00. Using the critical t-values table, at 95% confidence level and 35 degrees of freedom, the critical value is approximately 2.030. Since 3.00 > 2.030, the null hypothesis is reject, indicating a significant difference from the hypothesize mean.

Most Common FAQs

The p-value represents the probability of obtaining test results at least as extreme as the results observed, under the assumption that the null hypothesis is correct. A low p-value (typically below 0.05) indicates strong evidence against the null hypothesis, hence it is usually rejected.

Use a one-sample t-test when comparing the mean of a single sample to a known standard or hypothesized mean. Use a two-sample t-test when comparing the means of two independent groups to see if there is a statistically significant difference between them.

Yes, while the t-test is specifically design for means, the principles of hypothesis testing apply to other parameters such as proportions and variances. Which can also be tested using appropriate versions of hypothesis tests such as the z-test and F-test.

Related Calculators

PSI to ATM Calculator Online

Exponential Growth Decay Calculator Online

Microscope Resolution Calculator Online

True Position Calculator Online

Microstrip Width Calculator Online

Le Chatelier’s Principle Calculator Online

K and J Magnetics Calculator Online

Mass of Moon Calculator Online

Electrostatic Calculator Online

WKG Calculator Online

Leave a Comment Cancel reply

Save my name, email, and website in this browser for the next time I comment.

For optimal use, please visit DATAtab on your desktop PC!

Metric Variables:

Ordinal variables:, nominal variables:, hypothesis test calculator.

Do you want to calculate a hypothesis test such as a t-test , Chi Square test or an ANOVA ? You can do that easily here in the browser.

If you want to use your own data just clear the upper table

• Clear the table in the Hypothesis test calculator.
• Copy your data into the table.
• Select the variables.

In the hypothesis test calculator you can calculate e.g. a t-test, a chi-square test, a binomial test or an analysis of variance. If you need a more detailed explanation, you can find more information in the tutorials.

In order to use the hypothesis test calculator, you must first formulate your hypothesis and collect your data. DATAtab will then suggest the hypothesis test you need based on the data entered into the statistics calculator.

p value calculator

With the p value calculator you can calculate the p value for different tests. There is a wide range of methods for this. Just click on the variables you want to evaluate above and DATAtab will give you the tests you can use.

For example, if you select a metric and a categorical variable, the Independent t-Test calculator is automatically selected. If your data is not normally distributed, simply use the Mann-Whitney U-test calculator.

H0 and H1 calculator

With the h0 and h1 calculator for the different hypothesis test you can calculate the p-value which gives you an indication if you can reject the H0 or not.

Cite DATAtab: DATAtab Team (2024). DATAtab: Online Statistics Calculator. DATAtab e.U. Graz, Austria. URL https://datatab.net

Hypothesis Testing Calculator

Navigating hypothesis testing: unveiling the potential of the hypothesis testing calculator.

Embarking on the journey of statistical exploration, hypothesis testing stands out as an indispensable method for informed decision-making and drawing meaningful conclusions from data. Whether you find yourself in the academic realm, engaged in research endeavors, or navigating the professional landscape, having a trustworthy Hypothesis Testing Calculator in your statistical toolkit can prove to be a game-changer. Let’s delve into the intricacies of hypothesis testing and uncover how this calculator can be your ally in statistical analyses.

Demystifying Hypothesis Testing:

Null Hypothesis (H0): Positioned as the default assumption, the null hypothesis asserts the absence of any significant difference or effect and is commonly represented as H0.

Alternative Hypothesis (Ha): In direct contradiction to the null hypothesis, the alternative hypothesis posits the existence of a noteworthy difference or effect, denoted as Ha.

Significance Level (α): Acting as the predetermined threshold, typically set at 0.05 or 5%, the significance level plays a pivotal role in determining statistical significance. Should the calculated p-value fall below α, the null hypothesis is rejected.

p-value: Representing the likelihood of observing the results, or more extreme outcomes, under the assumption of the null hypothesis being true, a smaller p-value suggests the unlikelihood of the results occurring by chance.

Features that Define the Hypothesis Testing Calculator:

Input Parameters: The calculator demands input of sample data, selection of the test type (e.g., t-test, chi-square test), specification of null and alternative hypotheses, and determination of the significance level.

Calculations: Once armed with the requisite data and parameters, the calculator diligently executes statistical tests and computations. The output encompasses crucial details like the test statistic, degrees of freedom, and the all-important p-value.

Interpretation: Armed with the results, the calculator aids in the decision-making process, guiding whether to reject or accept the null hypothesis. An interpretation of the findings is provided, playing a pivotal role in drawing insightful conclusions.

Visual Representation: Some calculators go the extra mile by offering visual aids such as graphs or charts, facilitating a deeper understanding of data distribution and test outcomes.

Unveiling the Significance of the Hypothesis Testing Calculator:

In Scientific Research: Researchers spanning diverse fields leverage hypothesis testing to validate their hypotheses, thereby extracting meaningful insights from data.

In Quality Control: Industries rely on hypothesis testing as a quality assurance mechanism, ensuring the consistency and excellence of products and processes.

In Medical Studies: Within the realm of medical research, hypothesis testing serves as a critical tool for evaluating the effectiveness of treatments or interventions.

In Academics: Both students and educators find value in hypothesis testing as an educational tool, enabling the comprehension of statistical concepts and the conduct of experiments.

In Data-Driven Decision-Making: Businesses, keen on making decisions grounded in data, turn to hypothesis testing to navigate choices such as launching a new product based on comprehensive market research.

Concluding Insights:

The Hypothesis Testing Calculator emerges as a formidable ally, simplifying intricate statistical analyses and fostering data-driven decision-making. Whether you are in the midst of experimental undertakings, scrutinizing survey data, or overseeing quality control protocols, a solid understanding of hypothesis testing coupled with the use of this calculator empowers you to make well-informed choices. In doing so, you not only contribute to evidence-based research but also play a pivotal role in shaping decision-making processes across various domains.

Hypothesis Testing Calculator

Understanding Hypothesis Testing: A Guide to the Hypothesis Testing Calculator

Hypothesis testing is a crucial statistical method used to make informed decisions about data and draw conclusions. Whether you’re a student, researcher, or professional, a Hypothesis Testing Calculator can be an invaluable tool in your statistical toolkit. Let’s explore what hypothesis testing is and how this calculator can assist you:

Hypothesis Testing Basics:

• Null Hypothesis (H0): This is the default assumption or claim that there is no significant difference or effect. It’s often denoted as H0.
• Alternative Hypothesis (Ha): This is the statement that contradicts the null hypothesis. It suggests that there is a significant difference or effect. It’s denoted as Ha.
• Significance Level (α): This is the predetermined threshold (e.g., 0.05 or 5%) used to determine statistical significance. If the calculated p-value is less than α, you reject the null hypothesis.
• p-value: This is the probability of observing the results (or more extreme results) if the null hypothesis is true. A small p-value suggests that the results are unlikely under the null hypothesis.

Key Features of the Hypothesis Testing Calculator:

• Input Parameters: The calculator typically requires you to input sample data, choose the type of test (e.g., t-test, chi-square test), specify the null and alternative hypotheses, and set the significance level.
• Calculations: Once you input the data and parameters, the calculator performs the necessary statistical tests and calculations. It generates results such as the test statistic, degrees of freedom, and the p-value.
• Interpretation: Based on the results, the calculator helps you determine whether to reject or fail to reject the null hypothesis. It provides an interpretation of the findings, which is crucial for drawing conclusions.
• Visual Representation: Some calculators may offer visual aids like graphs or charts to help you better understand the data distribution and test results.

Significance of the Hypothesis Testing Calculator:

• Scientific Research: Researchers across various fields use hypothesis testing to validate their hypotheses and draw meaningful conclusions from data.
• Quality Control: Industries use hypothesis testing to ensure the quality and consistency of products and processes.
• Medical Studies: In medical research, hypothesis testing helps assess the effectiveness of treatments or interventions.
• Academics: Students and educators use hypothesis testing to teach and learn statistical concepts and conduct experiments.
• Data-Driven Decisions: Businesses use hypothesis testing to make data-driven decisions, such as whether to launch a new product based on market research.

Conclusion:

The Hypothesis Testing Calculator is a powerful tool that simplifies complex statistical analysis and enables data-driven decision-making. Whether you’re conducting experiments, analyzing survey data, or performing quality control, understanding hypothesis testing and using this calculator can help you make informed choices and contribute to evidence-based research and decision-making.

• Math Lessons
• Math Formulas
• Calculators

Math Calculators, Lessons and Formulas

It is time to solve your math problem

• HW Help (paid service)
• Statistics and probability
• T-test calculator

T-Test calculator

The Student's t-test is used to determine if means of two data sets differ significantly. This calculator will generate a step by step explanation on how to apply t - test.

• Factoring Polynomials
• Polynomial Roots
• Synthetic Division
• Polynomial Operations
• Graphing Polynomials
• Simplify Polynomials
• Generate From Roots
• Simplify Expression
• Multiplication / Division
• Addition / Subtraction
• Rationalize Denominator
• Simplifying
• Quadratic Equations Solver
• Polynomial Equations
• Solving Equations - With Steps
• Solving (with steps)
• Quadratic Plotter
• Factoring Trinomials
• Equilateral Triangle
• Right Triangle
• Oblique Triangle
• Square Calculator
• Rectangle Calculator
• Circle Calculator
• Hexagon Calculator
• Rhombus Calculator
• Trapezoid Calculator
• Triangular Prism
• Distance calculator
• Midpoint Calculator
• Triangle Calculator
• Graphing Lines
• Lines Intersection
• Two Point Form
• Line-Point Distance
• Parallel/Perpendicular
• Circle Equation
• Circle From 3 Points
• Circle-line Intersection
• Modulus, inverse, polar form
• Vectors (2D & 3D)
• Add, Subtract, Multiply
• Determinant Calculator
• Matrix Inverse
• Characteristic Polynomial
• Eigenvalues
• Eigenvectors
• Matrix Decomposition
• Limit Calculator
• Derivative Calculator
• Integral Calculator
• Arithmetic Sequences
• Geometric Sequences
• Find n th Term
• Degrees to Radians
• Trig. Equations
• Long Division
• Evaluate Expressions
• Fraction Calculator
• Greatest Common Divisor GCD
• Least Common Multiple LCM
• Prime Factorization
• Scientific Notation
• Percentage Calculator
• Dec / Bin / Hex
• Probability Calculator
• Probability Distributions
• Descriptive Statistics
• Standard Deviation
• Z - score Calculator
• Normal Distribution
• T-Test Calculator
• Correlation & Regression
• Simple Interest
• Compound Interest
• Amortization Calculator
• Annuity Calculator
• Work Problems

Hire MATHPORTAL experts to do math homework for you.

Prices start at $3 per problem.

Twelve younger adults and twelve older adults conducted a life satisfaction test. The data are presented in the table below. Compute the appropriate t-test.

Are the means between two data sets are significantly different at level $\alpha < 0.05$.

Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .

If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]

Email (optional)

Z-test Calculator

Table of contents

This Z-test calculator is a tool that helps you perform a one-sample Z-test on the population's mean . Two forms of this test - a two-tailed Z-test and a one-tailed Z-tests - exist, and can be used depending on your needs. You can also choose whether the calculator should determine the p-value from Z-test or you'd rather use the critical value approach!

Read on to learn more about Z-test in statistics, and, in particular, when to use Z-tests, what is the Z-test formula, and whether to use Z-test vs. t-test. As a bonus, we give some step-by-step examples of how to perform Z-tests!

Or you may also check our t-statistic calculator , where you can learn the concept of another essential statistic. If you are also interested in F-test, check our F-statistic calculator .

What is a Z-test?

A one sample Z-test is one of the most popular location tests. The null hypothesis is that the population mean value is equal to a given number, μ 0 \mu_0 μ 0 ​ :

We perform a two-tailed Z-test if we want to test whether the population mean is not μ 0 \mu_0 μ 0 ​ :

and a one-tailed Z-test if we want to test whether the population mean is less/greater than μ 0 \mu_0 μ 0 ​ :

Let us now discuss the assumptions of a one-sample Z-test.

When do I use Z-tests?

You may use a Z-test if your sample consists of independent data points and:

the data is normally distributed , and you know the population variance ;

the sample is large , and data follows a distribution which has a finite mean and variance. You don't need to know the population variance.

The reason these two possibilities exist is that we want the test statistics that follow the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) . In the former case, it is an exact standard normal distribution, while in the latter, it is approximately so, thanks to the central limit theorem.

The question remains, "When is my sample considered large?" Well, there's no universal criterion. In general, the more data points you have, the better the approximation works. Statistics textbooks recommend having no fewer than 50 data points, while 30 is considered the bare minimum.

Z-test formula

Let x 1 , . . . , x n x_1, ..., x_n x 1 ​ , ... , x n ​ be an independent sample following the normal distribution N ( μ , σ 2 ) \mathrm N(\mu, \sigma^2) N ( μ , σ 2 ) , i.e., with a mean equal to μ \mu μ , and variance equal to σ 2 \sigma ^2 σ 2 .

We pose the null hypothesis, H 0  ⁣  ⁣ :  ⁣  ⁣   μ = μ 0 \mathrm H_0 \!\!:\!\! \mu = \mu_0 H 0 ​ :   μ = μ 0 ​ .

We define the test statistic, Z , as:

x ˉ \bar x x ˉ is the sample mean, i.e., x ˉ = ( x 1 + . . . + x n ) / n \bar x = (x_1 + ... + x_n) / n x ˉ = ( x 1 ​ + ... + x n ​ ) / n ;

μ 0 \mu_0 μ 0 ​ is the mean postulated in H 0 \mathrm H_0 H 0 ​ ;

n n n is sample size; and

σ \sigma σ is the population standard deviation.

In what follows, the uppercase Z Z Z stands for the test statistic (treated as a random variable), while the lowercase z z z will denote an actual value of Z Z Z , computed for a given sample drawn from N(μ,σ²).

If H 0 \mathrm H_0 H 0 ​ holds, then the sum S n = x 1 + . . . + x n S_n = x_1 + ... + x_n S n ​ = x 1 ​ + ... + x n ​ follows the normal distribution, with mean n μ 0 n \mu_0 n μ 0 ​ and variance n 2 σ n^2 \sigma n 2 σ . As Z Z Z is the standardization (z-score) of S n / n S_n/n S n ​ / n , we can conclude that the test statistic Z Z Z follows the standard normal distribution N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , provided that H 0 \mathrm H_0 H 0 ​ is true. By the way, we have the z-score calculator if you want to focus on this value alone.

If our data does not follow a normal distribution, or if the population standard deviation is unknown (and thus in the formula for Z Z Z we substitute the population standard deviation σ \sigma σ with sample standard deviation), then the test statistics Z Z Z is not necessarily normal. However, if the sample is sufficiently large, then the central limit theorem guarantees that Z Z Z is approximately N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

In the sections below, we will explain to you how to use the value of the test statistic, z z z , to make a decision , whether or not you should reject the null hypothesis . Two approaches can be used in order to arrive at that decision: the p-value approach, and critical value approach - and we cover both of them! Which one should you use? In the past, the critical value approach was more popular because it was difficult to calculate p-value from Z-test. However, with help of modern computers, we can do it fairly easily, and with decent precision. In general, you are strongly advised to report the p-value of your tests!

p-value from Z-test

Formally, the p-value is the smallest level of significance at which the null hypothesis could be rejected. More intuitively, p-value answers the questions: provided that I live in a world where the null hypothesis holds, how probable is it that the value of the test statistic will be at least as extreme as the z z z - value I've got for my sample? Hence, a small p-value means that your result is very improbable under the null hypothesis, and so there is strong evidence against the null hypothesis - the smaller the p-value, the stronger the evidence.

To find the p-value, you have to calculate the probability that the test statistic, Z Z Z , is at least as extreme as the value we've actually observed, z z z , provided that the null hypothesis is true. (The probability of an event calculated under the assumption that H 0 \mathrm H_0 H 0 ​ is true will be denoted as P r ( event ∣ H 0 ) \small \mathrm{Pr}(\text{event} | \mathrm{H_0}) Pr ( event ∣ H 0 ​ ) .) It is the alternative hypothesis which determines what more extreme means :

• Two-tailed Z-test: extreme values are those whose absolute value exceeds ∣ z ∣ |z| ∣ z ∣ , so those smaller than − ∣ z ∣ -|z| − ∣ z ∣ or greater than ∣ z ∣ |z| ∣ z ∣ . Therefore, we have:

The symmetry of the normal distribution gives:

• Left-tailed Z-test: extreme values are those smaller than z z z , so
• Right-tailed Z-test: extreme values are those greater than z z z , so

To compute these probabilities, we can use the cumulative distribution function, (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , which for a real number, x x x , is defined as:

Also, p-values can be nicely depicted as the area under the probability density function (pdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) , due to:

Two-tailed Z-test and one-tailed Z-test

With all the knowledge you've got from the previous section, you're ready to learn about Z-tests.

• Two-tailed Z-test:

From the fact that Φ ( − z ) = 1 − Φ ( z ) \Phi(-z) = 1 - \Phi(z) Φ ( − z ) = 1 − Φ ( z ) , we deduce that

The p-value is the area under the probability distribution function (pdf) both to the left of − ∣ z ∣ -|z| − ∣ z ∣ , and to the right of ∣ z ∣ |z| ∣ z ∣ :

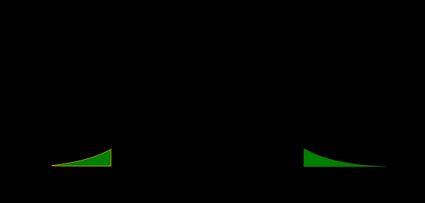
• Left-tailed Z-test:

The p-value is the area under the pdf to the left of our z z z :

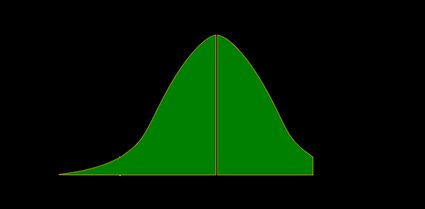
• Right-tailed Z-test:

The p-value is the area under the pdf to the right of z z z :

The decision as to whether or not you should reject the null hypothesis can be now made at any significance level, α \alpha α , you desire!

if the p-value is less than, or equal to, α \alpha α , the null hypothesis is rejected at this significance level; and

if the p-value is greater than α \alpha α , then there is not enough evidence to reject the null hypothesis at this significance level.

Z-test critical values & critical regions

The critical value approach involves comparing the value of the test statistic obtained for our sample, z z z , to the so-called critical values . These values constitute the boundaries of regions where the test statistic is highly improbable to lie . Those regions are often referred to as the critical regions , or rejection regions . The decision of whether or not you should reject the null hypothesis is then based on whether or not our z z z belongs to the critical region.

The critical regions depend on a significance level, α \alpha α , of the test, and on the alternative hypothesis. The choice of α \alpha α is arbitrary; in practice, the values of 0.1, 0.05, or 0.01 are most commonly used as α \alpha α .

Once we agree on the value of α \alpha α , we can easily determine the critical regions of the Z-test:

To decide the fate of H 0 \mathrm H_0 H 0 ​ , check whether or not your z z z falls in the critical region:

If yes, then reject H 0 \mathrm H_0 H 0 ​ and accept H 1 \mathrm H_1 H 1 ​ ; and

If no, then there is not enough evidence to reject H 0 \mathrm H_0 H 0 ​ .

As you see, the formulae for the critical values of Z-tests involve the inverse, Φ − 1 \Phi^{-1} Φ − 1 , of the cumulative distribution function (cdf) of N ( 0 , 1 ) \mathrm N(0, 1) N ( 0 , 1 ) .

How to use the one-sample Z-test calculator?

Our calculator reduces all the complicated steps:

Choose the alternative hypothesis: two-tailed or left/right-tailed.

In our Z-test calculator, you can decide whether to use the p-value or critical regions approach. In the latter case, set the significance level, α \alpha α .

Enter the value of the test statistic, z z z . If you don't know it, then you can enter some data that will allow us to calculate your z z z for you:

• sample mean x ˉ \bar x x ˉ (If you have raw data, go to the average calculator to determine the mean);
• tested mean μ 0 \mu_0 μ 0 ​ ;
• sample size n n n ; and
• population standard deviation σ \sigma σ (or sample standard deviation if your sample is large).

Results appear immediately below the calculator.

If you want to find z z z based on p-value , please remember that in the case of two-tailed tests there are two possible values of z z z : one positive and one negative, and they are opposite numbers. This Z-test calculator returns the positive value in such a case. In order to find the other possible value of z z z for a given p-value, just take the number opposite to the value of z z z displayed by the calculator.

Z-test examples

To make sure that you've fully understood the essence of Z-test, let's go through some examples:

• A bottle filling machine follows a normal distribution. Its standard deviation, as declared by the manufacturer, is equal to 30 ml. A juice seller claims that the volume poured in each bottle is, on average, one liter, i.e., 1000 ml, but we suspect that in fact the average volume is smaller than that...

Formally, the hypotheses that we set are the following:

H 0  ⁣ :   μ = 1000  ml \mathrm H_0 \! : \mu = 1000 \text{ ml} H 0 ​ :   μ = 1000  ml

H 1  ⁣ :   μ < 1000  ml \mathrm H_1 \! : \mu \lt 1000 \text{ ml} H 1 ​ :   μ < 1000  ml

We went to a shop and bought a sample of 9 bottles. After carefully measuring the volume of juice in each bottle, we've obtained the following sample (in milliliters):

1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 \small 1020, 970, 1000, 980, 1010, 930, 950, 980, 980 1020 , 970 , 1000 , 980 , 1010 , 930 , 950 , 980 , 980 .

Sample size: n = 9 n = 9 n = 9 ;

Sample mean: x ˉ = 980   m l \bar x = 980 \ \mathrm{ml} x ˉ = 980   ml ;

Population standard deviation: σ = 30   m l \sigma = 30 \ \mathrm{ml} σ = 30   ml ;

And, therefore, p-value = Φ ( − 2 ) ≈ 0.0228 \text{p-value} = \Phi(-2) \approx 0.0228 p-value = Φ ( − 2 ) ≈ 0.0228 .

As 0.0228 < 0.05 0.0228 \lt 0.05 0.0228 < 0.05 , we conclude that our suspicions aren't groundless; at the most common significance level, 0.05, we would reject the producer's claim, H 0 \mathrm H_0 H 0 ​ , and accept the alternative hypothesis, H 1 \mathrm H_1 H 1 ​ .

We tossed a coin 50 times. We got 20 tails and 30 heads. Is there sufficient evidence to claim that the coin is biased?

Clearly, our data follows Bernoulli distribution, with some success probability p p p and variance σ 2 = p ( 1 − p ) \sigma^2 = p (1-p) σ 2 = p ( 1 − p ) . However, the sample is large, so we can safely perform a Z-test. We adopt the convention that getting tails is a success.

Let us state the null and alternative hypotheses:

H 0  ⁣ :   p = 0.5 \mathrm H_0 \! : p = 0.5 H 0 ​ :   p = 0.5 (the coin is fair - the probability of tails is 0.5 0.5 0.5 )

H 1  ⁣ :   p ≠ 0.5 \mathrm H_1 \! : p \ne 0.5 H 1 ​ :   p  = 0.5 (the coin is biased - the probability of tails differs from 0.5 0.5 0.5 )

In our sample we have 20 successes (denoted by ones) and 30 failures (denoted by zeros), so:

Sample size n = 50 n = 50 n = 50 ;

Sample mean x ˉ = 20 / 50 = 0.4 \bar x = 20/50 = 0.4 x ˉ = 20/50 = 0.4 ;

Population standard deviation is given by σ = 0.5 × 0.5 \sigma = \sqrt{0.5 \times 0.5} σ = 0.5 × 0.5 ​ (because 0.5 0.5 0.5 is the proportion p p p hypothesized in H 0 \mathrm H_0 H 0 ​ ). Hence, σ = 0.5 \sigma = 0.5 σ = 0.5 ;

• And, therefore

Since 0.1573 > 0.1 0.1573 \gt 0.1 0.1573 > 0.1 we don't have enough evidence to reject the claim that the coin is fair , even at such a large significance level as 0.1 0.1 0.1 . In that case, you may safely toss it to your Witcher or use the coin flip probability calculator to find your chances of getting, e.g., 10 heads in a row (which are extremely low!).

What is the difference between Z-test vs t-test?

We use a t-test for testing the population mean of a normally distributed dataset which had an unknown population standard deviation . We get this by replacing the population standard deviation in the Z-test statistic formula by the sample standard deviation, which means that this new test statistic follows (provided that H₀ holds) the t-Student distribution with n-1 degrees of freedom instead of N(0,1) .

When should I use t-test over the Z-test?

For large samples, the t-Student distribution with n degrees of freedom approaches the N(0,1). Hence, as long as there are a sufficient number of data points (at least 30), it does not really matter whether you use the Z-test or the t-test, since the results will be almost identical. However, for small samples with unknown variance, remember to use the t-test instead of Z-test .

How do I calculate the Z test statistic?

To calculate the Z test statistic:

• Compute the arithmetic mean of your sample .
• From this mean subtract the mean postulated in null hypothesis .
• Multiply by the square root of size sample .
• Divide by the population standard deviation .
• That's it, you've just computed the Z test statistic!

Here, we perform a Z-test for population mean μ. Null hypothesis H₀: μ = μ₀.

Alternative hypothesis H₁

Significance level α

The probability that we reject the true hypothesis H₀ (type I error).

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 12: Significance tests (hypothesis testing)

About this unit.

Significance tests give us a formal process for using sample data to evaluate the likelihood of some claim about a population value. Learn how to conduct significance tests and calculate p-values to see how likely a sample result is to occur by random chance. You'll also see how we use p-values to make conclusions about hypotheses.

The idea of significance tests

• Simple hypothesis testing (Opens a modal)
• Idea behind hypothesis testing (Opens a modal)
• Examples of null and alternative hypotheses (Opens a modal)
• P-values and significance tests (Opens a modal)
• Comparing P-values to different significance levels (Opens a modal)
• Estimating a P-value from a simulation (Opens a modal)
• Using P-values to make conclusions (Opens a modal)
• Simple hypothesis testing Get 3 of 4 questions to level up!
• Writing null and alternative hypotheses Get 3 of 4 questions to level up!
• Estimating P-values from simulations Get 3 of 4 questions to level up!

Error probabilities and power

• Introduction to Type I and Type II errors (Opens a modal)
• Type 1 errors (Opens a modal)
• Examples identifying Type I and Type II errors (Opens a modal)
• Introduction to power in significance tests (Opens a modal)
• Examples thinking about power in significance tests (Opens a modal)
• Consequences of errors and significance (Opens a modal)
• Type I vs Type II error Get 3 of 4 questions to level up!
• Error probabilities and power Get 3 of 4 questions to level up!

Tests about a population proportion

• Constructing hypotheses for a significance test about a proportion (Opens a modal)
• Conditions for a z test about a proportion (Opens a modal)
• Reference: Conditions for inference on a proportion (Opens a modal)
• Calculating a z statistic in a test about a proportion (Opens a modal)
• Calculating a P-value given a z statistic (Opens a modal)
• Making conclusions in a test about a proportion (Opens a modal)
• Writing hypotheses for a test about a proportion Get 3 of 4 questions to level up!
• Conditions for a z test about a proportion Get 3 of 4 questions to level up!
• Calculating the test statistic in a z test for a proportion Get 3 of 4 questions to level up!
• Calculating the P-value in a z test for a proportion Get 3 of 4 questions to level up!
• Making conclusions in a z test for a proportion Get 3 of 4 questions to level up!

Tests about a population mean

• Writing hypotheses for a significance test about a mean (Opens a modal)
• Conditions for a t test about a mean (Opens a modal)
• Reference: Conditions for inference on a mean (Opens a modal)
• When to use z or t statistics in significance tests (Opens a modal)
• Example calculating t statistic for a test about a mean (Opens a modal)
• Using TI calculator for P-value from t statistic (Opens a modal)
• Using a table to estimate P-value from t statistic (Opens a modal)
• Comparing P-value from t statistic to significance level (Opens a modal)
• Free response example: Significance test for a mean (Opens a modal)
• Writing hypotheses for a test about a mean Get 3 of 4 questions to level up!
• Conditions for a t test about a mean Get 3 of 4 questions to level up!
• Calculating the test statistic in a t test for a mean Get 3 of 4 questions to level up!
• Calculating the P-value in a t test for a mean Get 3 of 4 questions to level up!
• Making conclusions in a t test for a mean Get 3 of 4 questions to level up!

Number Line

• arithmetic\:mean\:1,\:2,\:3,\:4,\:5,\:6
• geometric\:mean\:\left\{0.42,\:0.52,\:0.58,\:0.62\right\}
• quadratic\:mean\:-4,\:5,\:6,\:9
• median\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• mode\:\left\{90,\:94,\:53,\:68,\:79,\:94,\:87,\:90,\:70,\:69,\:65,\:89,\:85\right\}
• minimum\:-4,\:5,\:6,\:9
• maximum\:\frac{31}{100},\:\frac{23}{105},\:\frac{31}{205},\:\frac{54}{205}
• mid\:range\:1,\:2,\:3,\:4,\:5,\:6
• range\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• standard\:deviation\:\:\left\{1,\:7,\:-3,\:4,\:9\right\}
• variance\:1,\:2,\:3,\:4,\:5,\:6
• lower\:quartile\:-4,\:5,\:6,\:9
• upper\:quartile\:\left\{0.42,\:0.52,\:0.58,\:0.62\right\}
• interquartile\:range\:1,\:2,\:3,\:4,\:5,\:6
• midhinge\:\left\{90,\:94,\:53,\:68,\:79,\:84,\:87,\:72,\:70,\:69,\:65,\:89,\:85\right\}
• What is the best calculator for statistics?
• Symbolab offers an online calculator specifically for statistics that can perform a wide range of calculations, including standard deviation, variance, range and normal distribution. It also provides detailed step-by-step solutions.
• What is statistics?
• Statistics is the branch of mathematics that deals with the collection, analysis, interpretation, presentation, and organization of data. There are two main branches of statistics: descriptive statistics, and inferential statistics.
• What is descriptive statistics?
• Descriptive statistics is a branch of statistics that deals with summarizing, organizing and describing data. Descriptive statistics uses measures such as central tendency (mean, median, and mode) and measures of variability (range, standard deviation, variance) to give an overview of the data.
• What is inferential statistics?
• Inferential statistics is a branch of statistics that deals with making predictions and inferences about a population based on a sample of data. Inferential statistics uses probability theory and statistical models to make predictions and inferences about a population.
• What is the difference between statistics and probability?
• Statistics is the branch of mathematics dealing with the collection, analysis, interpretation, presentation, and organization of data, while probability is the branch of mathematics dealing with the likelihood of occurrence of different events.

statistics-calculator

• Lies, Damned Lies, and Statistics Statistics is about analyzing data, for instance the mean is commonly used to measure the “central tendency” of...

Please add a message.

Message received. Thanks for the feedback.

Z-test: One Population Proportion

Instructions: This calculator conducts a Z-test for one population proportion (p). Please select the null and alternative hypotheses, type the hypothesized population proportion \(p_0\), the significance level \(\alpha\), the sample proportion or number o favorable cases, and the sample size, and the results of the z-test for one proportion will be displayed for you:

Z-Test for One Population Proportion

More about the z-test for one population proportion so you can better interpret the results obtained by this solver: A z-test for one proportion is a hypothesis test that attempts to make a claim about the population proportion (p) for a certain population attribute (proportion of males, proportion of people underage). The test has two non-overlapping hypotheses, the null and the alternative hypothesis. The null hypothesis is a statement about the population proportion, which corresponds to the assumption of no effect, and the alternative hypothesis is the complementary hypothesis to the null hypothesis. The main properties of a one sample z-test for one population proportion are:

• Depending on our knowledge about the "no effect" situation, the z-test can be two-tailed, left-tailed or right-tailed
• The main principle of hypothesis testing is that the null hypothesis is rejected if the test statistic obtained is sufficiently unlikely under the assumption that the null hypothesis is true
• The sampling distribution used to construct the test statistics is approximately normal
• The p-value is the probability of obtaining sample results as extreme or more extreme than the sample results obtained, under the assumption that the null hypothesis is true
• In a hypothesis tests there are two types of errors. Type I error occurs when we reject a true null hypothesis, and the Type II error occurs when we fail to reject a false null hypothesis

The formula for a z-statistic is

The null hypothesis is rejected when the z-statistic lies on the rejection region, which is determined by the significance level (\(\alpha\)) and the type of tail (two-tailed, left-tailed or right-tailed).

This one proportion z test calculator will allow you to compute the critical values are p-values for this one sample proportion test, that will help you decide whether or not the sample data provides enough evidence to reject the null hypothesis. If instead, what you want to do is to compare two sample proportions, you can use this z-test for two proportions calculator , which will help you assess whether the two sample proportions differ significantly.

Related Calculators

log in to your account

Reset password.

Hypothesis Testing

Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.

A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.

What is Hypothesis Testing in Statistics?

Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.

Hypothesis Testing Definition

Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.

Null Hypothesis

The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.

Alternative Hypothesis

The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.

Hypothesis Testing P Value

In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.

Hypothesis Testing Critical region

All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.

Hypothesis Testing Formula

Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:

• z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
• t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
• \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.

We will learn more about these test statistics in the upcoming section.

Types of Hypothesis Testing

Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.

Hypothesis Testing Z Test

A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:

• One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
• Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing t Test

The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.

• One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
• Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).

Hypothesis Testing Chi Square

The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.

One Tailed Hypothesis Testing

One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.

Right Tailed Hypothesis Testing

The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:

\(H_{0}\): The population parameter is ≤ some value

\(H_{1}\): The population parameter is > some value.

If the test statistic has a greater value than the critical value then the null hypothesis is rejected

Left Tailed Hypothesis Testing

The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:

\(H_{0}\): The population parameter is ≥ some value

\(H_{1}\): The population parameter is < some value.

The null hypothesis is rejected if the test statistic has a value lesser than the critical value.

Two Tailed Hypothesis Testing

In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:

\(H_{0}\): the population parameter = some value

\(H_{1}\): the population parameter ≠ some value

The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.

Hypothesis Testing Steps

Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:

• Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
• Step 2: Set up the alternative hypothesis.
• Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
• Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
• Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.

Hypothesis Testing Example

The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.

Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.

Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.

Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.

1 - \(\alpha\) = 1 - 0.05 = 0.95

0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.

Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.

z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).

\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15

z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56

Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.

Hypothesis Testing and Confidence Intervals

Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.

Related Articles:

• Probability and Statistics
• Data Handling

Important Notes on Hypothesis Testing

• Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
• It involves the setting up of a null hypothesis and an alternate hypothesis.
• There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
• Hypothesis testing can be classified as right tail, left tail, and two tail tests.

Examples on Hypothesis Testing

• Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
• Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
• Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.

go to slide go to slide go to slide

Book a Free Trial Class

FAQs on Hypothesis Testing

What is hypothesis testing.

Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.

What is the z Test in Hypothesis Testing?

The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.

What is the t Test in Hypothesis Testing?

The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?

The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).

What is the p Value in Hypothesis Testing?

The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.

What is One Tail Hypothesis Testing?

When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.

What is the Alpha Level in Two Tail Hypothesis Testing?

To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.

• 1-800-234-2933
• [email protected]

Hypothesis Testing for a proportion Calculator

How does the Hypothesis Testing for a proportion Calculator work?

What 2 formulas are used for the hypothesis testing for a proportion calculator, what 6 concepts are covered in the hypothesis testing for a proportion calculator.

An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.

Our Services

• All Subjects
• A.I. Training Data and Analytics
• Get Paid as an Affiliate

Top Categories

• Trigonometry
• Pre-Algebra
• Pre-Calculus
• Post a Math Problem

Question.AI-Math Calculator 4+

Scan&solve all subject problem.

• #5 in Education
• 4.6 • 19.5K Ratings
• Offers In-App Purchases

Screenshots

Description.

Experience the future of communication with Question.AI, the ultimate AI Chatbot app that's revolutionizing the way you gather information, communicate, and stay informed across various facets of life. Whether you're a student, a professional at work, an inquisitive mind, or a business enthusiast, our app is designed to make your life easier, smarter, and more efficient in any context. 【Key Features】 - Simplicity at its Best: Seeking answers has never been easier. Just ask your questions, and our intuitive AI will promptly provide you with accurate responses. No need for complex commands or jargon - it's like having a knowledgeable friend by your side 24/7. - Your Personal Assistant: From quick facts to in-depth research, Question.AI is your personal assistant ready to assist you. Need a definition, explanation, or summary? Count on us to deliver information tailored to your needs. - Global Connectivity: Break language barriers effortlessly. With the ability to translate into 140+ languages, Question.AI ensures you can communicate and connect with individuals from all around the world. Expand your horizons and broaden your perspectives with ease. - Intelligent Writing: Enhance your writing with AI-powered suggestions. Whether you're crafting an email, composing a report, or writing creatively, our app's intelligent writing feature offers insightful recommendations to make your content shine. - Adaptable Across Occasions: Question.AI is your versatile companion across various occasions, whether it's for studying, working, managing your business, or simply enhancing your daily life. We're here to assist you in every scenario. 【Why Choose Question.AI?】 With a commitment to excellence and user satisfaction, Question.AI stands out as the ultimate AI Chatbot app: - User-Friendly: Our user-centric design prioritizes simplicity and accessibility, ensuring a seamless experience for users of all ages. - Instant Insights: Get answers in real-time, allowing you to make informed decisions and impress others with your newfound knowledge. - Trusted Accuracy: Our AI's responses are backed by robust algorithms, ensuring that the information you receive is reliable and up-to-date. - Empowering Communication: Break down language barriers, foster connections, and engage with a global community effortlessly. - Unleash Creativity: Elevate your writing and communication skills with AI-powered suggestions that refine and elevate your content. Ready to embark on a journey of knowledge and connection? Download Question.AI now and experience the future of communication in the palm of your hand. Get started today! 【Contact us】 Email: [email protected] Official Website: www.questionai.com Instagram: @question.ai_app YouTube: @QuestionAI-Official Facebook: bit.ly/QuestionAI_FB TikTok: @question.ai_app Discord: bit.ly/QuestionAI_DC Messenger Group: https://m.me/j/AbaNe6U1Rhv5NAiL/ Privary Policy: https://www.questionai.com/privacy-policy Terms and Conditions: https://www.questionai.com/useTerm

Version 2.6.0

We’ve optimized the user experience. Update now!

Ratings and Reviews

19.5K Ratings

Literal LIFE SAVER

Your math teacher don't explain stuff like this and you know it. All you gotta do is just take a picture and it'll explain everything step by step. The app is free, but the pro cost money. Yes, the pro helps, but the app itself without any add-ons is still amazing and literally life-saving. If you are ever in doubt in math just snap a pic. And to make it even better is does others subject if you need any more help. Its just so awesome in general , like whoever came up with this stuff is a genius and so relatable. The videos would be so helpful but I don't pay for pro because my mom won't let me😭 Anywho, the step by step process is really easy to understand as well. Just get this app if you are in need of a math tutor, and tbh I think everyone needs a lil help on math especially, just consider downloading this app. Super easy to use and super easy to understand. THANK YOU DEARLY QUESTION A.I!!!🤗🤗

Developer Response ,

We're thrilled to know that you're satisfied with our app! Your positive experience is our greatest reward. Thank you for choosing us!

Love this app!!

I love this app so much usually you have to pay a monthly fee but with this you don’t, I didn’t buy it at first. I thought that we would have to pay monthly and I didn’t feel like getting the app but I gave it out a try. After I gave it a few tries and math questions I realize it really does help and that I love it so much,being in middle school and having tough math helps me so much with this even though I don’t really read the videos on how to do it sure helps with the answers and that is what it’s great about this app because you can help me with with my homework and if I need help it’ll give me. I love this app so much definitely recommended you don’t have to pay any monthly fee and this is the first app. I’ve actually waited five stars and left a comment because usually these apps aren’t good, but this one is amazing. Love it so much. Thanks.

We have always focused on providing high-quality service and user experience. Thank you for your recognition and support!

I’ve never been so greatful towards an app before, usually there was a deal with other apps that you had only a few tries before you had to pay for the full thing or wait your time…which 90% of the time didn’t even give you an answer or help… I’ve never had something this smooth be so dang helpful 😭❤️ Not only did it help me pass my test (88% omg 😍) but it also gave helpful advice and dumbed it down for me so i didn’t have to read through everything. Quite literally gave me the information i wanted and also the answer which is AMAZING 😨❤️Helped me better understand the questions SO THANK YOU 🙏 will definitely be using this on math 🥶 hoping for the same smoothness on math since it’s what i struggle with but overall just from a first time use i’m deeply thankful for this app!! 😭🙏❤️

Thank you for your positive feedback! I'm delighted to hear that you're enjoying the application. Please feel free to share any suggestions you have directly, and I'll do my best to assist or pass them along to the appropriate team for consideration.

App Privacy

The developer, 3HOUSE , indicated that the app’s privacy practices may include handling of data as described below. For more information, see the developer’s privacy policy .

Data Used to Track You

The following data may be used to track you across apps and websites owned by other companies:

Data Not Linked to You

The following data may be collected but it is not linked to your identity:

• Identifiers

Privacy practices may vary, for example, based on the features you use or your age. Learn More

Information

English, Arabic, Dutch, French, German, Indonesian, Italian, Japanese, Korean, Malay, Portuguese, Russian, Simplified Chinese, Spanish, Traditional Chinese, Vietnamese

• Question.AI DPro - Monthly $9.99
• Question.AI Plus-Monthly $11.99
• Question.AI Pro-Monthly $8.99
• Question.AI DPro - yearly $99.99
• Question.AI Plus-Yearly $99.99
• Question.AI Plus-yearly $34.99
• Question.AI DPro - Monthly New $9.99
• Questionai Pro - Monthly $9.99
• Question.AI Plus Special Offer $9.99
• Developer Website
• App Support
• Privacy Policy

You Might Also Like

Answer.AI - Your AI tutor

Quizard AI - Scan and Solve

Ai Homework Helper: Scan Solve

TutorEva: Campus AI Study Help

Pic Answer - AI Solver

Special Features

Vendor voice.

Bored students can now enjoy Sonic 2 on TI-84 Plus CE calculators, thanks to port

Blast (processing) from the past.

Retro interview Just a few weeks ago, Sonic the Hedgehog 2 was ported to the TI-84 Plus CE graphing calculator.

Playing retro games on calculators is nothing new, with Tetris, Breakout, and even Super Mario Bros 3 having fan-made ports to Texas Instruments' popular calculator.

However, no games featuring the blue hedgehog ever made it to the small screen – until now. GitHub user grubbyplaya, who also goes by grubbycoder, ported 1992's Sonic the Hedgehog 2 to the device, making it the first Sonic platformer game we're aware of now available for the calculator. Source and binaries have been released ; yes, it's completely unofficial.

The dev was inspired to port it after watching a video by the This Does Not Compute YouTube channel on the history of gaming on calculators. When the mini documentary mentioned that some of TI's calculators used 8-bit Zilog Z80 and 16/32-bit Motorola 68000 CPUs, it caught grubbycoder's attention. Those chips were also used by Sega's Master System and Genesis (or Mega Drive for those outside North America), so porting Sonic from one of those consoles to the TI calculator should be reasonably fun to do.

"That really piqued my interest, since I already knew the processors that Sega's retro game consoles used: The Z80 for the Master System, and the M68K for the Genesis," the programmer said in his documentation of the port.

"Aside from that, I also really wanted to make my own calculator game, or at least port an existing one," grubbycoder told The Register . "Doom's a bit too big to fit into the 84 Plus CE's storage, so that's part of the reason why I stuck with games in the 8-bit to 16-bit range. Of course, I did rule out any 16-bit games later on."

I really wanted to make my own calculator game, or at least port an existing one

However, grubbycoder didn't port the Sega Genesis version of Sonic 2; instead, he used the version made for the 8-bit Sega Master System and Game Gear. This was down to the fact that the biggest TI calculators based on the 68000 CPU didn't have a good enough screen resolution for the 68000-based Genesis version of the game.

By contrast, the TI-84 Plus CE with its Zilog eZ80 chip (which is essentially a 24-bit Z80 with extra bells and whistles) has a 320 by 240 pixel display, which is more than enough for the 8-bit Master System and Game Gear version.

Choosing the TI-84 Plus CE also meant grubbycoder's choices for what Sonic games to port were limited. Today, the only fully disassembled Sonic game on the Master System is Sonic the Hedgehog 2, so that was the one he went with.

"Most of the other games people really want, like Sonic 1 8-bit and Sonic Triple Trouble, only have partial disassemblies," grubbycoder says. "If I were to start porting them, most of my work would just go to reverse-engineering the entire game."

Porting even a disassembled game was a challenge

On paper, it would seem the TI-84 Plus CE is perfect for an 8-bit Sonic game. Its eZ80 clocks in at 48MHz, much higher than the Master System's Z80A at 3.58MHz, and has 256KB of RAM, more than ten times as much as the Master System's combined 8KB of RAM and 16KB of VRAM.

However, those hardware advantages are dinged by wait states that could drag down the eZ80's actual clock speed to 12MHz; a per-file size cap that forces the use of multiple files for any data larger than 64KB; and the complete lack of any console-like graphics acceleration. The extra processing oomph needs to be used on filling those gaps.

Plus, the TI-84 Plus CE will crash if any game code tries to access what it expects to be an I/O port on the Sega console – such as if the game tries to talk to the console's audio system, color palette hardware, and VRAM. Those IO accesses needed to be rerouted and translated on the calculator to prevent a crash and make Sonic 2 play as expected.

Additionally, grubbycoder had to use an assembler for the TI calculator that was different to the one used by the Sonic 2 disassembly project he based his port on, which brought about compatibility hurdles, and he wasn't an expert on the Z80 nor the TI-84 Plus CE.

"At first, I only had a very beginner-level knowledge of Z80 assembly, which meant I made some really stupid decisions with handling some stuff which came back to bite me later," he says.

"As the complexity of emulating features of the Master System grew, I eventually had moderate-level knowledge of how the TI-84 Plus CE works," grubbycoder told us.

Assembling the game from the disassembly source was the first task, and while the TI-friendly SPASM-ng assembler did much of that work, grubbycoder still had to review 20,000 lines of code to make sure everything was compatible with the TI-84 Plus CE.

Getting around the I/O accesses wasn't terribly difficult as it turned out, because the calculator's hardware supports memory-mapped I/O requests. The port just needed tweaking so that its I/O port requests go to the calculator's memory-mapped IO locations, with some glue code to act as a compatibility layer. The game thinks it's running on and talking to Sega hardware, but is actually interacting with a TI calculator.

"It was mostly just a minor inconvenience," grubbycoder says, noting that video color palettes were the most complex to implement at the hardware translation layer.

Unfortunately, there were two parts of the port that really couldn't work they way they did on the Master System. Firstly, the Master System used ROM banking to swap in and out the memory map chunks of data as needed, since the old-school console could only address 64KB of data at any one time and the game is much larger than that. On the TI-84 Plus CE, this is relatively slow because it relies on flash storage to copy data into RAM when needed, since there wasn't enough room, even with 256KB of RAM, to put every single bank into memory all at once.

The other problematic part was the renderer, since the TI-84 Plus CE has no graphics acceleration hardware to speak of. A 16-bit multiplication instruction present in the eZ80 helped speed up sprite and tile plotting in software, in terms of calculating the location of the graphics.

That said, handling the tile-based background was a challenge. Sega's console hardware provides lots of support for rapidly arranging and scrolling Sonic's levels, and that acceleration needed to be emulated on the calculator's eZ80.

Screenshot of the port's graphics software renderer mid-development

Grubbycoder implemented this with a 56KB framebuffer in the TI's VRAM and a caching system that reduced the tile rendering time by a factor of eight, allowing the game to actually be playable.

Starting up the port and getting the intro rendering

While not a perfect conversion, on the whole it runs, it's a cool programming project, and it's not even that different from the original version. "Technically, the 84 Plus CE port retains 90 to 95 percent of the original 8-bit Sonic 2 code," grubbycoder says. 

There's no audio since the calculator doesn't have speakers, and deleting the audio code and materials made the game smaller at least. The framerate is lower than the 60 FPS Master System owners would have enjoyed. "On base 84 Plus CEs, which was the model emulated in testing, the game runs at about 53 percent speed with the normal build," the dev says.

There is a fast model of the game that runs at 74 percent speed, but this version has no enemies, bosses, or even the goalposts that signal the end of levels, meaning even the first level cannot be completed.

"The slowdown is almost entirely due to ROM banking, specifically swapping in banks that contain logic for Sonic, all the Badniks, and every gimmick in the game," grubbycoder says.

"If the calculator didn't have wait states, then it wouldn't be a problem at all, but other solutions include converting those banks to run in the 84 Plus CE's 24-bit mode, so they just be jumped to instead of loading them in all at once."

But technically, if one very bored student with only a calculator to fiddle with wanted to beat Sonic the Hedgehog 2 from start to finish and would tolerate a somewhat bad framerate, it's very possible. Though nowadays high-end calculators equipped with Arm CPU cores, such as the Nspire, can run actual Genesis games, and may be the better option for those looking for the best calculator gaming experience, grubbycoder says.

Still, the developer is looking to add more Sonic games to the 2015-era TI-84 Plus CE. "In the future, I would like to try remaking some more obscure Sonic games for the calculator," he says.

"They wouldn't be the platformers everyone's familiar with, but some of the LCD games by Tiger Electronics and the Sonic Adventure Gamebook series are what I'm mostly interested in remaking." ®

• Texas Instruments
• Video Game Console

Narrower topics

• Activision Blizzard

Send us news

Other stories you might like

Activist investor pressures texas instruments to stop spending cash on fabs, sega grabs tech layoff baton and dumps couple hundred euro staff, husqvarna ports doom to a robot lawnmower – not, thankfully, its chainsaws, modernizing storage for the age of ai.

Boss fight between Donkey Kong champ and leaderboard org ends with settlement

Hackers mod a sony playstation portal to run psp games, if you're gonna use ai-made stuff in your game, you better tell us, says steam, $6.2b in profit wasn't enough: nvidia hikes geforce now prices for canada and europe, unity talks of price cap and fees for only largest games developers, guild behind actors' strike fears video game workers also at risk from ai, start rummaging: atari's new 2600+ console supports vintage cartridges, the painstation runs windows xp because of course it does.

• Advertise with us

Our Websites

• The Next Platform
• Blocks and Files

Your Privacy

• Cookies Policy
• Privacy Policy
• Ts & Cs

Copyright. All rights reserved © 1998–2024